Calculus III 11.05 Lines and Planes in Three Dimensions

Previous	Calculus III 11.04 The Cross Product for Two Vectors in Three Dimensions
Next	Calculus III 11.06 Surfaces in Three Dimensions

Calculus III 11.5 Lines and Planes in Three Dimensions

• Use parametric equations to describe a line in three dimensions.
• Describe a line in three dimensions with a linear equation.
• Sketch the plane given by a linear equation.
• Find the distances between points, planes, and lines in three dimensions.

Lines in Three Dimensions

Line \(L\) and its direction vector \(v\). Figure 11.5.1

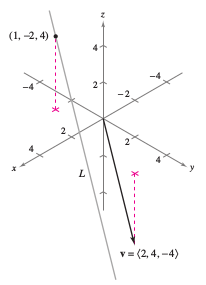
On a plane, slope is used to determine a line's equation. In three dimensions vectors are used to determine a line's equation. Consider the line \(L\) through the point \(P(x_{1}, y_{1},z_{1})\) and parallel to the vector \(\textbf{v}= \langle a,b,c \rangle\), as shown in Figure 11.5.1. The vector \(\textbf{v}\) is a direction vector for the line \(L\), and \(a\), \(b\), and \(c\) are direction numbers. Here, the line \(L\) is described as all points \(Q(x,y,z)\) for which the vector \(\vec{PQ}\) is parallel to \(\textbf{v}\). This means that \(\vec{PQ}\) is a scalar multiple for \(\textbf{v}\) and can be written as \(\vec{PQ} = t\textbf{v}\), where \(t\) is a real number scalar. \(\vec{PQ} = \langle x-x_{1}, y - y_{1}, z - z_{1} \rangle = \langle at, bt, ct \rangle = t\textbf{v}\) Equating the corresponding components produces the parametric equations that describe a line in three dimensions.

Theorem 11.5.1 Parametric Equations for a Line in Three Dimensions

A line \(L\) parallel to the vector \(\textbf{v}= \langle a,b,c \rangle\) and passing through the point \(P(x_{1}, y_{1},z_{1})\) is described by the parametric equations

\(x=x_{1}+at,\:y=y_{1}+bt,\text{ and }z=z_{1}+ct\).

If the direction numbers \(a\), \(b\), and \(c\) are all nonzero the parameter \(t\) can be removed to produce symmetric equations for the line.

$$\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\:\:\:\: \color{red}{\text{Symmetric equations}} $$

Parametric and symmetric equations for any given line are not unique. In Example 11.5.1 letting \(t=1\) in the parametric equations yields the point (3,2,0). Using this point with the direction numbers \(a=2\), \(b=4\), and \(c=-4\) would produce different parametric equations

\(x=3+2t\), \(y=2+4t\), and \(z=-4t\).

Example 11.5.1 Finding Parametric and Symmetric Equations

The vector v is parallel to the line \(L\) Figure 11.1.7

Find parametric and symmetric equations for the line \(L\) that passes through the point (1,-2,4) and is parallel to \(\textbf{v}= \langle 2,4,-4 \rangle\), as shown in figure 11.5.2. Solution To find the parametric equations use the coordinates \(x_{1}=1\), \(y_{1}=-2\), \(z_{1}=4\) and the direction numbers \(a=2\), \(b=4\), and \(c=-4\). \(x=1+2t,\:y=-2+4t,\:z=4-4t\:\:\:\: \color{red}{\text{Parametric equations}} \) Because \(a\), \(b\), and \(c\) are all nonzero, the symmetric equations are $$\frac{x-1}{2}=\frac{y+2}{4}=\frac{z-4}{-4}\:\:\:\: \color{red}{\text{Symmetric equations}} $$

Example 11.5.2 Parametric Equations for a Line Through Two Points

Find the parametric equations for a line that passes through the points

(-2,1,0) and (1,3,5).

Solution Begin by using the points \(P(-2,1,0)\) and \(Q(1,3,5)\) to find a direction vector for the line passing through \(P\) and \(Q\).

\(\textbf{v}=\vec{PQ}= \langle 1-(-2),3-1,5-0 \rangle = \langle 3,2,5 \rangle = \langle a,b,c \rangle \)

Using the direction numbers \(a=3\), \(b=2\), and \(c=5\) with the point \(P(-2,1,0)\) yields the parametric equations

\(x=-2+3t\), \(y=1+2t\), and \(z=5t\).

As \(t\) varies over all real numbers, the parametric equations in Example 11.5.2 determine the points \((x, y, z )\) on the line. Note that when \(t= 0\) and \(t=1\) the original points (-2,1,0) and (1,3,5) are produced.

Planes in Three Dimensions

The normal vector \(\textbf{b}\) is orthogonal to each vector \(\vec{PQ}\) on the plane. Figure 11.5.3

A normal vector is perpendicular to the plane, not parallel to it as in previous examples. The equation for a plane in three dimensions can be obtained from a point in a plane and a normal vector. Consider the plane containing the point \(P(x_{1}, y_{1},z_{1})\) having a nonzero normal vector \(\textbf{n}=\langle a,b,c \rangle \) as shown in Figure 11.5.3. The plain is defined as all points \(Q(x,y,z)\) for which \(\vec{PQ}\) is orthogonal to \(\textbf{n}\). Applying the dot product produces \(\textbf{n} \cdot \vec{PQ}\) \(= 0\) \(\langle a,b,c \rangle \cdot \langle x-x_{1}, y - y_{1}, z - z_{1} \rangle \ \) \(= 0 \) \(a(x-x_{1}) +b(y-y_{1}) +c(z-z_{1}) \) \(= 0 \) The third equation for the plane is said to be in standard form.

Theorem 11.5.2 Standard Equation for a Plane in Three Dimensions

The plane containing the point \((x_{1}, y_{1},z_{1})\) and having normal vector

\(\textbf{n}=\langle a,b,c \rangle \)

can be represented by a plane's equation in standard form

\(a(x-x_{1}) +b(y-y_{1}) +c(z-z_{1}) = 0 \).

The general form for a plane in three dimensions can be produced by regrouping the terms

\(ax+by+cz+d=0 \:\:\:\: \color{red}{\text{General form for a plane equation}} \)

Use the coefficients for \(x\), \(y\), and \(z\) to find the general form for the plane's equation

\(\textbf{n}=\langle a,b,c \rangle \).

Example 11.5.3 Finding an Equation for a Plane in Three Dimensions

A plane determined by \(\textbf{u}\) and \(\textbf{v}\) Figure 11.5.4

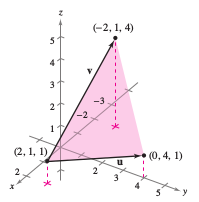
Find the general equation for the plane containing the points (2,1,1), (0,4,1), and (-2,1,4). Solution To apply Theorem 11.5.2 a point on the plane and a vector normal to the plane are needed. There are three choices for the point, but no normal vector is given. Use the given points to create cross products for vectors \(\textbf{u}\) and \(\textbf{v}\), as shown in Figure 11.5.4. The components for vectors \(\textbf{u}\) and \(\textbf{v}\) are \(\textbf{u} = \langle 0-2,4-1,1-1 \rangle = \langle -2,3,0 \rangle\) \(\textbf{v} = \langle -2-2,1-1,4-1 \rangle = \langle -4,0,3 \rangle\) the cross product is \( \textbf{n} \) \(=\textbf{u} \times \textbf{v} \) $$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ -2 & 3 & 0 \\ -4 & 0 & 3 \end{vmatrix} $$ \(= 9\textbf{i} + 6\textbf{j} + 12 \textbf{k} \) \(= \langle a,b,c \rangle \) is normal to the given plane. Using the direction numbers for \( \textbf{n} \) and the point \((x_{1},xy_{1},z_{1})=(2,1,1)\), the plane's equation is \(a(x-x_{1})+b(y-y_{1})+c(z-z_{1}) \) \(=0\) \(9(x-2)+6(y-1)+12(z-1) \) \(=0\) \(9x+6y+12z-36\) \(=0\) \(3x+2y+4z-12 \) \(=0.\) As a check see if each point satisfies the equation \(3x+2y+4z-12 =0.\)

The angle \(\theta\) between two planes Figure 11.5.5

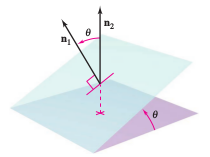
Two distinct planes in three dimensions are either parallel or intersect on a line. The angle \((0 \leqslant \theta \leqslant \pi/2)\) between two intersecting planes can be determined from their normal vectors, as shown in Figure 11.5.5. If vectors \( \textbf{n}_{1} \) and \( \textbf{n}_{2} \) are normal to two intersecting planes, then the angle \(\theta\) between the normal vectors is equal to the angle between the planes and is $$ \cos \theta = \frac{|\textbf{n}_{1} \cdot \textbf{n}_{2} |}{\|\textbf{n}_{1} \| \|\textbf{n}_{2} \|}. \:\:\:\: \color{red}{\text{Angle between two planes}} $$ Two planes with normal vectors \( \textbf{n}_{1} \) and \( \textbf{n}_{2} \) are perpendicular when \(\textbf{n}_{1} \cdot \textbf{n}_{2} = 0 \). parallel when \(\textbf{n}_{1} \) is a scalar multiple for \( \textbf{n}_{2} \).

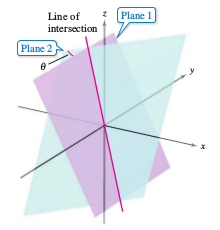
Example 11.5.4 Finding the Intersection Line between Two Planes

Figure 11.5.6

Find the angle between the two planes \(x-2y+z=0\) and \(2x+3y-2z=0\). Then find parametric equations for the intersection line, as shown in Figure 11.5.6. Solution Normal vectors for the planes are \(\textbf{n}_{1}= \langle 1,-2,1 \rangle\) and \(\textbf{n}_{2}= \langle 2,3,2 \rangle\). The angle between the two planes is determined as follows. $$ \cos \theta = \frac{|\textbf{n}_{1} \cdot \textbf{n}_{2} |}{\|\textbf{n}_{1} \| \|\textbf{n}_{2} \|} = \frac{|-6|}{\sqrt{6}\sqrt{17}}=\frac{6}{\sqrt{102}} \approx 0.59409. $$ The intersecting line can be found by simultaneously solving the two linear equations representing the planes. \(x-2y+z=0 \) $$\Rightarrow $$ \(-2x+4y-2z=0 \) \(2x+3y-2z=0\) \(\underline{2x+3y-2z=0}\) \(7y-4z=0 \) \(\Rightarrow \) $$y=\frac{4z}{7} $$ Substituting \(y=4z/7\) back into either equation yields \(x=z/7\). Letting \(t=z/7\) produces the parametric equations \(x=t\), \(y=4t\), and \(z=7t\:\:\:\: \color{red}{\text{Intersection Line.}} \) which indicate that 1, 4, and 7 are direction numbers for the intersection line.

Sketching Planes in Three Dimensions

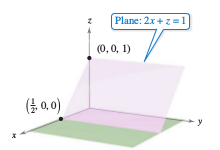
When a plane in three dimensions intersects a coordinate plane the intersection line is called the trace. To sketch a plane in three dimensions all its traces are needed. Consider the plane

\(3x+2y+14z=12.\:\:\:\: \color{red}{\text{Plane equation.}} \)

The \(xy\)-trace is found by letting \(z=0\) and sketching the line

\(3x+2y=12.\:\:\:\: \color{red}{xy\text{-trace}} \)

on the \(xy\)-plane. This intersects the \(x\)-axis at (4,0,0) and the \(y\)-axis at (0,6,0). Find the \(yz\) and \(xz\) traces, then shade the triangular region in the first octant, as shown in Figure 11.5.7.

Figure 11.5.7

Plane \(2x+z=1\) is parallel to the \(y\)-axis. Figure 11.5.8

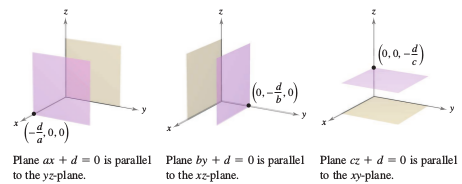
When a plane's equation has a missing variable, such as \(2x+z=1\) the plane must be parallel to the axis represented by the missing variable, as shown in Figure 11.5.8. When two variables are missing, such as \(ax+d-0\) then it is parallel to the coordinate plane represented by the missing variables, as shown in Figure 11.5.9.

Figure 11.5.9

Distances Between Points, Planes, and Lines in Three Dimensions

The distance between a point and a plane. Figure 11.5.10

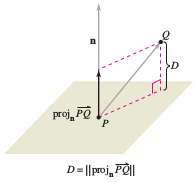
Consider two problem with distance in three dimensions: (1) finding the distance between a point and a plane, and (2) finding the distance between a point and a line. The first is solved with the dot product for two vectors, and the second problem uses the cross product. The distance \(D\) between a point \(Q\) and a plane is the length for the shortest line segment connecting \(Q\) to the plane, as shown in Figure 11.5.10. For any point \(P\) in the plane, you can find this distance by projecting the vector \(\vec{PQ}\) onto the normal vector \(\textbf{n}\). This projection's length is the desired distance.

Theorem 11.5.3 Distance Between a Point and a Plane

The distance between a plane and a point \(Q\), not in the plane, is

$$D=\| \text{proj}_{\textbf{n}} \vec{PQ} \| = \frac{| \vec{PQ} \cdot \textbf{n} |}{\| \textbf{n} \|}$$

where \(P\) is a point in the plane and \(\textbf{n}\) is normal to the plane.

To find a point in the plane \(ax+by+cz+d=0\), where \(a \ne 0\), let \(y=0\) and \(z=0\). This yields the equation \(ax+d=0\) and the point

$$\left ( -\frac{d}{a},0,0 \right ) $$

lies in the plane.

Example 11.5.5 Finding the Distance Between a Point and a Plane

Find the distance between the point \(Q(1,5,-4)\) and the plane \(3x-y+2z=6\).
Solution The vector \(\textbf{n}=\langle 3,-1,2\rangle\) is normal to the plane. To find an arbitrary point in the plane, let \(y=0\) and \(z=0\) to produce the point \(P(2,0,0)\). The vector from \(P\) to \(Q\) is

\(\vec{PQ}\)	\(=\langle 1-2,5-0,-4-0 \rangle \)
	\(= \langle -1,5,-4 \rangle\).

Applying the Distance Formula produces

$$D=\frac{| \vec{PQ} \cdot \textbf{n}| }{\| \textbf{n} \|}= \frac{| \langle -1,5,-4 \rangle \cdot \langle 3,-1,2\rangle|}{\sqrt{9+1+4}}=\frac{|-3-5-8|}{\sqrt{14}}=\frac{16}{\sqrt{14}} \approx 4.28 $$

Using Theorem 11.5.3, the distance between the point \(Q(x_{0},y_{0},z_{0})\) and the plane \(ax+by+cz+d=0\) is

$$D=\frac{|a(x_{0}-x_{1})+b(y_{0}-y_{1})+c(z_{0}-z_{1}) |}{\sqrt{a^{2}+b^{2}+c^{2}}} $$

or

$$D=\frac{|ax_{0}+by_{0}+cz_{0}+d |}{\sqrt{a^{2}+b^{2}+c^{2}}}\:\:\:\: \color{red}{\text{Distance between a point and a plane}} $$

where \(P(x_{1},xy_{1},z_{1}) \) is a point in the plane and \(d=-(ax_{1}+by_{1}+cz_{1})\).

Example 11.5.6 Finding the Distance Between Two Parallel Planes

The distance between the parallel planes is \(\approx\) 2.14 Figure 11.5.11

Two parallel planes, \(3x-y+2z-6=0\) and \(6x-2y+4z+4=0\), are shown in Figure 11.5.11. Find the distance between the planes. Solution Choose an arbitrary point in the first plane, say, \((x_{0},y_{0},z_{0})=(2,0,0)\). From the second plane determine the direction numbers as \(a=6\), \(b=-2\), \(c=4\), and \(d=4\). Applying Theorem 11.5.3 produces \(D\) $$=\frac{|ax_{0}+by_{0}+cz_{0}+d |}{\sqrt{a^{2}+b^{2}+c^{2}}} $$ $$=\frac{|6(2)+(-2)(0)+(4)(0)+4|}{\sqrt{6^{2}+(-2)^{2}+4^{2}}} $$ $$= \frac{16}{\sqrt{56}}=\frac{8}{\sqrt{14}}\approx 2.14.$$

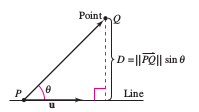
Theorem 11.5.4 Distance Between a Point and a Line in Three Dimensions

The distance between a point and a line. Figure 11.5.12

The distance between a point \(Q\) and a line in space is $$D= \frac{\| \vec{PQ} \times \textbf{u} \|}{\| \textbf{u} \| } $$ where \( \textbf{u} \) is a direction vector for the line and \(P\) is a point on the line. Proof Let \(D\) be the distance between the point \(Q\) and the line, as shown in Figure 11.5.12. Then \(D=\| \vec{PQ} \| \sin \theta \), where \(\theta\) is the angle between \( \textbf{u} \) and \( \vec{PQ} \). By Theorem 11.4.2, Property 2, \(\| \textbf{u} \| \| \vec{PQ} \| = \sin \theta = \| \textbf{u} \times \vec{PQ} \| = \| \vec{PQ} \times \textbf{u} \| \). Therefore, $$D=\| \vec{PQ} \| \sin \theta = \frac{\| \vec{PQ} \times \textbf{u} \|}{\| \textbf{u} \| } $$

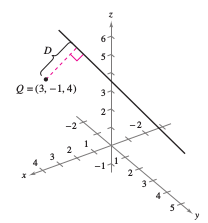
Example 11.5.7 Finding the Distance Between a Point and a Line

The distance between the point \(Q\) and the line \(\sqrt{6} \approx 2.45\). Figure 11.5.13

Find the distance between the point \(Q(3,-1,4)\) and the line \(x=-2+3t\), \(y=-2t\), and \(z=1+4t\). Solution Using the direction numbers 3, -2, and 4, a direction vector for the line is \(\textbf{u} = \langle 3,-2,4 \rangle\). To find a point on the line, let \(t=0\) and produce \(P=(-2,0,1)\). This produces \( \vec{PQ} = \langle 3 - (-2), -1-0,4-1 \rangle = \langle 5,-1,3 \rangle \) the cross product is $$\vec{PQ} \times \textbf{u} = \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 5 & -1 & 3 \\ 3 & -2 & 4 \end{vmatrix} = 2\textbf{i}-11\textbf{j}-7\textbf{k}= \langle 2,-11,-7 \rangle $$ Applying Theorem 11.5.4 yields the distance $$D= \frac{\| \vec{PQ} \times \textbf{u} \|}{\| \textbf{u} \| } = \frac{\sqrt{174}}{\sqrt{29}}= \sqrt{6} \approx 2.45$$ as shown in Figure 11.5.13.

Internal Links

Parent Article: Calculus III 11 Vectors and Spacial Geometry