Calculus III 11.06 Surfaces in Three Dimensions

Previous	Calculus III 11.05 Lines and Planes in Three Dimensions
Next	Calculus III 11.07 Cylindrical and Spherical Coordinates

Calculus III 11.6 Surfaces in Three Dimensions

• Cylindrical Surface equations.
• Quadric Surfaces equations.
• Surfaces for Revolution equations.

Cylindrical Surface

The red lines are rulings parallel to the \(z\)-axis. Figure 11.6.1

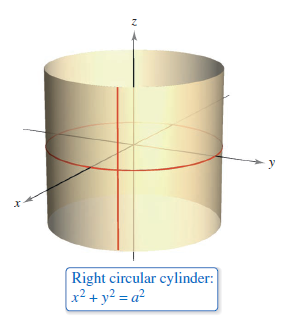
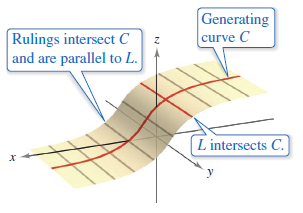
Consider the familiar right-angle circular cylinder shown in Figure 11.6.1. The cylinder was generated by rotating a vertical line around the circle \(x^{2}/a^{2}+y^{2}/a^{2}=1\) in the \(xy\)-plane. This circle is a generating curve for the cylinder, as indicated in Definition 11.6.1. Definition 11.6.1 The Cylinder[1] Let \(C\) be a curve in a plane and let \(L\) be a line not in a parallel plane. The set containing all lines parallel to \(L\) and intersecting \(C\) is a cylinder. The curve \(C\) is the generating curve (or directrix) for the cylinder, and the parallel lines are rulings. Let \(h= height\), \(r=radius\) Area Closed Cylinder is \(2\pi r ( r + h) \) Open Cylinder is \(2\pi r h \) Volume is \(V=\pi r^{2} h \).

Right Cylinder: A cylinder with rulings perpendicular to the coordinate plane containing \(C\). Figure 11.6.2

This discussion is restricted to right cylinders -- cylinders whose rulings are perpendicular to the coordinate plane containing \(C\), as shown in Figure 11.6.2. Note the rulings intersect \(C\) and are parallel to the line \(L\). To find an equation for a cylinder, note that you can generate any ruling by fixing the values for \(x\) and \(y\) and then allowing \(z\) to take on all real values. In this sense, the value for \(z\) is arbitrary and is, therefore, not included in the equation. The equation for a cylinder is simply the equation for its generating curve. $$ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}}= 1\:\:\:\: \color{red}{\text{ Equation for a cylinder in three dimensions. }} $$

Example 11.6.1 Sketching a Cylinder

Sketch the surface represented by each equation.
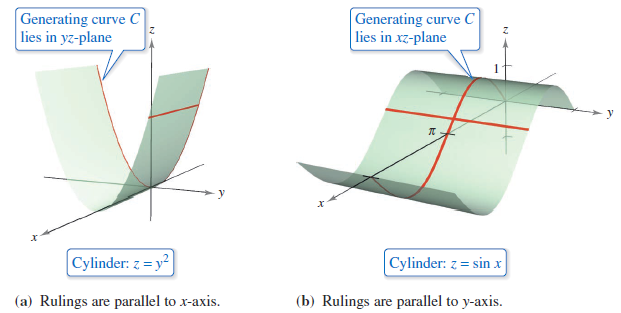
a. \(z=y^{2}\) b. \(z=\sin x\), \(0 \leqslant x \leqslant 2 \pi\).
Solution
a. The graph is a cylinder whose generating curve, \(z=y^{2}\), is a parabola in the \(yz\)-plane. The rulings on the cylinder are parallel to the \(x\)-axis, as shown in Figure 11.6.3(a).
b. The graph is a cylinder generated by the sine curve in the \(xz\)-plane. The rulings are parallel to the \(y\)-axis, as shown in Figure 11.6.3(b).

Right Cylinder: A cylinder with rulings perpendicular to the coordinate plane containing \(C\).
Figure 11.6.3

Quadric Surface

Definition 11.6.2 Quadric Surface[2]

The equation for a quadric surface in three dimensions is a second-degree equation in three variables. The general form is

\( Ax^{2}+By^{2}+Cz^{2}+Dxy+Exz+Fyz+Gx+Hy+Iz+J=0 \)

Quadric surfaces come in six basic types: ellipsoid, hyperboloid of one sheet, hyperboloid of two sheets, elliptic cone, elliptic paraboloid, and hyperbolic paraboloid, as shown in Figures 11.6.4 and 11.6.5.

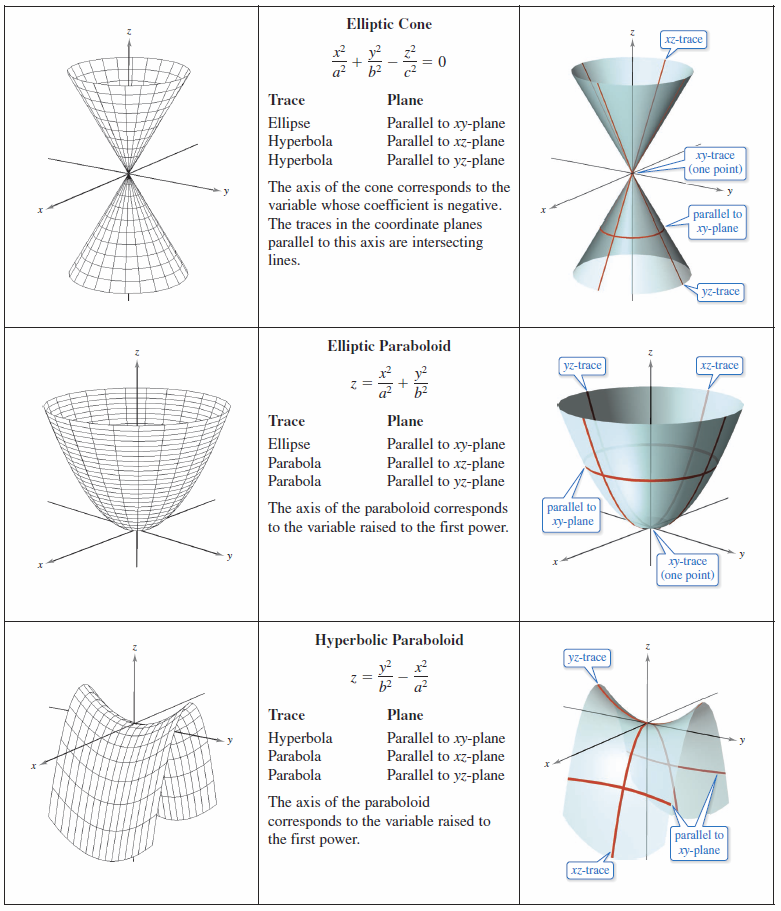
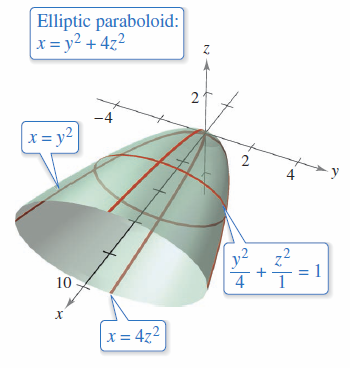
The intersection between a surface and a plane is called the 'trace of the surface in the plane. The traces for quadric surfaces are conics. Sketching quadric surfaces is easier when the axes are aligned along the coordinate planes. Be aware that any surface can be oriented along any line. When a surface is oriented along a different axis, its standard equation will change accordingly, as illustrated in Examples 11.6.2 and 11.6.3. The quadric surfaces mentioned in Definition 11.6.2, their traces, and standard equations, are shown in Figures 11.6.4 and 11.6.5.

Figure 11.6.4

Figure 11.6.5

Example 11.6.2 Sketching a Quadric Surface

Figure 11.6.6

Sketch the surface given by the following equation and identify the type \(4x^{2}-3y^{2}+12z^{2}+12=0\). Solution Begin by writing the equation in standard form \(4x^{2}-3y^{2}+12z^{2}+12\) \(= 0\)     Original Equation $$-\frac{x^{2}}{3}+\frac{y^{2}}{4}-z^{2}-1 $$ $$=0$$     Divide by -12 $$\frac{y^{2}}{4}-\frac{x^{2}}{3}-\frac{z^{2}}{1} $$ $$=1$$     Standard form. To aid in sketching first find the traces along the coordinate planes. 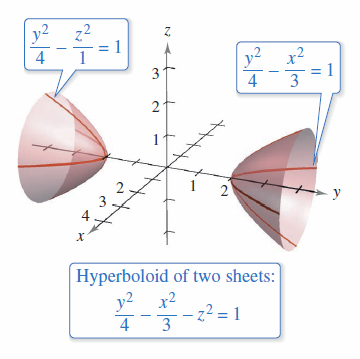\(xy-\text{trace}\:(z=0):\) $$\frac{y^{2}}{4}-\frac{x^{2}}{3} = 1$$     Hyperbola \(xz-\text{trace}\:(y=0):\) $$\frac{x^{2}}{3}+\frac{z^{2}}{1} = -1 $$     No trace \(yz-\text{trace}\:(x=0):\) $$\frac{y^{2}}{4}-\frac{z^{2}}{1} = 1 $$     Hyperbola The sketch in Figure 11.6.6 matches the Hyperboloid of Two Sheets found in Figure 11.6.4 aligned along the \(y\)-axis.

Example 11.6.3 Sketching a Quadric Surface

Figure 11.6.7

Sketch the surface given by the following equation and identify the type \(x-y^{2}-4z^{2}=0\). Solution Because \(x\) is raised only to the first power, the surface is a paraboloid. The paraboloid is aligned along the \(x\)-axis. In standard form, the equation is \(x=y^{2}+4z^{2}. \:\:\:\: \) Standard Form Two orthogonal traces are listed below. \(xy\text{-trace } (z=0): \) \(x=y^{2} \)     Parabola \(xz\text{-trace } (y=0): \) \(x=4z^{2} \)     Parabola \(\text{ parallel to }yz\text{-plane } (x=4):\) $$\frac{y^{2}}{4}+\frac{z^{2}}{1}=1 $$     Ellipse The surface is an elliptic paraboloid, as shown in Figure 11.6.7.

Some second-degree equations in three dimensions are not described by any basic quadratic surface. For example,

\(x^{2}+y^{2}+z^{2} = 0\)	A single point in three dimensions
\(x^{2}+y^{2} = 1\)	Right circular cylinder

Example 11.6.4 A Quadric Surface Not Centered at the Origin

An ellipsoid centered at (2,-1,1) Figure 11.6.8

Classify and sketch the surface \( x^{2}+2y^{2}+z^{2} - 4x +4y-2z+3 = 0. \) Solution This equation can be converted into standard form by completing the square. Begin by grouping terms and factoring where possible. \( x^{2}-4x +2(y^{2}+2y )+z^{2}-2z = -3 \) Complete the square for each variable and write the equation in standard form. 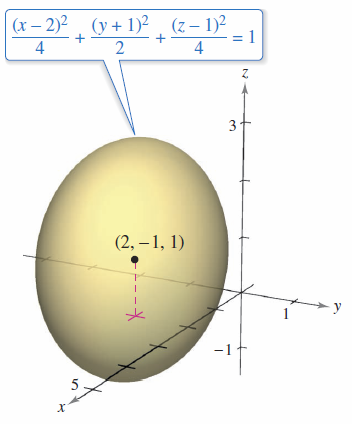\((x^{2}-4x+ \:\:\:)+2(y^{2}+2y+\:\:\: )+(z^{2}-2z+\:\:\:) \) \(=-3 \) \((x^{2}-4x+ 4)+2(y^{2}+2y+1 )+(z^{2}-2z+1) \) \(=-3+4+2+1 \) \( (x-2)^{2}+2(y+1)^{2}+(z-1)^{2} \) \(=4 \) $$ \frac{(x-2)^{2}}{4}+\frac{(y+1)^{2}}{2}+\frac{(z-1)^{2}}{4} $$ \(=1\) The quadric surface is an ellipsoid centered at (2, -1, 1), as shown in Figure 11.6.8.

Surface for Revolution

Figure 11.6.9

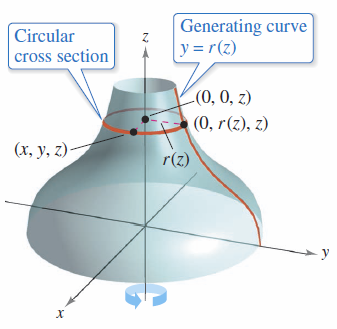
Given a rotated surface, find its equation. Consider the graph for a radius function \( y=r(z) \)    Generating curve in the \(xy\)-plane. When this graph is rotated about the \(z\)-axis, it forms a surface for rotation, as shown in Figure 11.6.9. The trace for the surface in the plane \(z=z_{0}\) is a circle whose radius is \(r(z_{0})\) and whose equation is \(x^{2}+y^{2}=[r(z_{0})]^{2}\).    Circular trace in plane: \(z=z_{0}\) Replacing \(z_{0}\) with \(z\) produces an equation that is valid for all values in \(z\). Equations for rotated surfaces for the \(x\) and \(y\) axes and the results are summarized in Definition 11.6.3.

Definition 11.6.3 Surfaces for Revolution

If the graph for a radius function is rotated about a coordinate axis, the equation for the resulting surface has a form listed below.

1. Revolution about the \(x\)-axis: \(y^{2}+z^{2}= [r(x)]^{2}\)
2. Revolution about the \(y\)-axis: \(x^{2}+z^{2}= [r(y)]^{2}\)
3. Revolution about the \(z\)-axis: \(x^{2}+y^{2}= [r(z)]^{2}\)

Example 11.6.5 Finding an Equation for a Rotated Surface

Figure 11.6.10

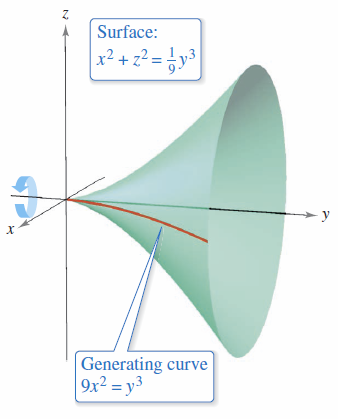
Find an equation for the rotated surface formed by revolving (a) the graph for \(y=1/z\) about the \(z\)-axis and (b) the graph for \(9x^{2}=y^{3}\) about the \(y\)-axis. Solution a. An equation for the rotated surface formed by revolving the graph for $$ y=\frac{1}{z}\:\:\:\:\color{red}{ \text{ Radius function}}$$ about the \(z\)-axis \(x^{2}+y^{2}=[r(z)]^{2}\:\:\:\:\color{red}{ \text{ Revolved about the }z\text{-axis}}\) $$x^{2}+y^{2}= \left( \frac{1}{z} \right)^{2}\:\:\:\:\color{red}{ \text{ Substitute }1/z \text{ for } r(z)} $$ b. To find an equation for the surface formed by revolving the graph for \(9x^{2}=y^{3}\) about the \(y\)-axis, solve for \(x\) in \(y\) terms to produce $$x=\frac{1}{3}y^{3/2}=r(y).\:\:\:\:\color{red}{ \text{ Radius function }}$$ The equation for this surface is $$x^{2}+z^{2}=[r(y)]^{2}\:\:\:\:\color{red}{ \text{ Revolved about the }y\text{-axis}}$$ $$x^{2}+z^{2}=\left(\frac{1}{3}y^{3/2} \right )^{2}\:\:\:\:\color{red}{ \text{ Substitute }1/3y^{3/2}\text{ for } r(y).}$$ $$x^{2}+z^{2}=\frac{1}{9}y^{3}\:\:\:\:\color{red}{ \text{ Equation for the surface }}$$ The graph is shown in Figure 11.6.10.

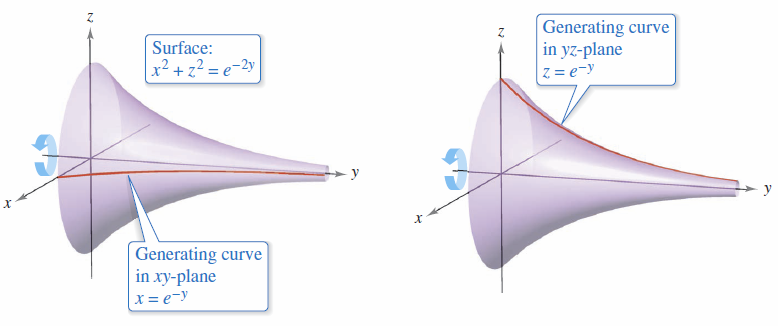
The generating curve for a rotated surface is not unique. For instance, the surface

\(x^{2}+z^{2}=e^{-2y} \)

can be formed by revolving either the graph for

\(x=e^{-y} \)

about the \(y\)-axis or the graph for

\(z=e^{-y} \)

about the \(y\)-axis, as shown in Figure 11.6.11.

Figure 11.6.11

Example 11.6.6 Finding a Generating Curve

Figure 11.6.12

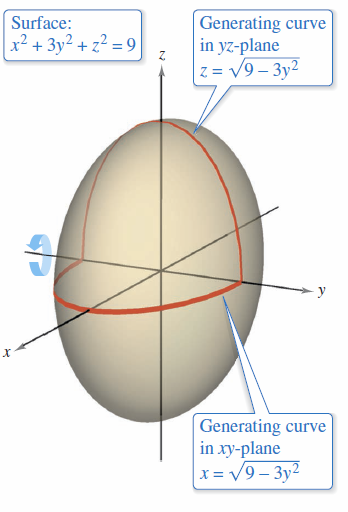
Find a generating curve and the revolution axis for the surface \( x^{2}+3y^{2}+z^{2}=9 \) Solution Because the coefficients for \(x^{2}\) and \(z^{2}\) are equal the third form in Definition 11.6.3 matches the equation and it can be written as \( x^{2}+z^{2}=9-3y^{2} \) The graph rotates about the \(y\)-axis. The generating curve can be chosen from the \(xy\)-plane or \(yz\)-plane trace. \( x^{2}=9-3y^{2} \:\:\:\: \color{red}{ xy\text{-plane trace }} \) \( z^{2}=9-3y^{2} \:\:\:\: \color{red}{ yz\text{-plane trace }} \) The first trace generates a semi-ellipse curve \( x= \sqrt{9-3y^{2}}\:\:\:\: \color{red}{ \text{Generating curve }} \) as shown in Figure 11.6.12.

Internal Links

Parent Article: Calculus III 11 Vectors and Spacial Geometry