Calculus III 12.02 Differentiation and Integration for Vector-Valued Functions

Previous	Calculus III 12.01 Vector-Valued Functions
Next	Calculus III 12.03 Velocity and Acceleration

12.2 Differentiation and Integration for Vector-Valued Functions

• Differentiate a vector-valued function.
• Integrate a vector-valued function.

Differentiation for Vector-Valued Functions

Definition 12.2.1 Derivative for a Vector-Valued Function

Figure 12.2.1

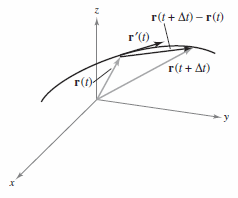
The derivative for a vector-valued function \( \textbf{ r } \) is $$ \textbf{r}^{\prime} (t) = \lim_{\Delta t \rightarrow 0} \frac{ \textbf{r} (t+ \Delta t) - \textbf{r}(t)}{\Delta t} $$ for all \(t\) for which the limit exists. If \( \textbf{r}^{\prime} (t) \) exists, the \(\textbf{r} \) is differentiable at \(t\). If \( \textbf{r}^{\prime} (t) \) exists for all \(t\) on an open interval \(I\), then \( \textbf{r} \) is differentiable on the interval \(I\). Differentiability for vector-valued functions can be extended to closed intervals by considering one-sided limits. $$\textbf{r}^{\prime} = \frac{d}{dt}[\textbf{r}(t)],\: \frac{d\textbf{r}}{dt} \text{, and }D_{t}[\textbf{r}(t)] \:\:\:\: \color{red}{ \text{ Derivative for vector-valued function in other notation.}}$$ Vector-valued functions are differentiated on a component-by-component basis by using the Distributive Property. Consider the function \( \textbf{r}(t)=f(t)\textbf{i}+g(t)\textbf{j} \). Applying the derivative's distributed property produces. \( \textbf{r}^{\prime} (t) \) $$= \lim_{\Delta t \rightarrow 0} \frac{ \textbf{r}(t+ \Delta t) - \textbf{r}(t)}{\Delta t} $$ $$= \lim_{\Delta t \rightarrow 0} \frac{ f(t+ \Delta t)\textbf{i} + g(t+ \Delta t)\textbf{j} - f(t)\textbf{i} - g(t)\textbf{j}}{\Delta t} $$ $$= \lim_{\Delta t \rightarrow 0} \left \{ \left[ \frac{ f(t+ \Delta t) - f(t)}{\Delta t} \right]\textbf{i} + \left[ \frac{ g(t+ \Delta t) - g(t)}{\Delta t} \right]\textbf{j} \right \}$$ $$ =\left \{ \lim_{\Delta t \rightarrow 0} \left[ \frac{ f(t+ \Delta t) - f(t)}{\Delta t} \right]\textbf{i} \right \} + \left \{\lim_{\Delta t \rightarrow 0} \left[ \frac{ g(t+ \Delta t) - g(t)}{\Delta t} \right]\textbf{j} \right \} $$ \(= f^{\prime}(t)\textbf{i} + g^{\prime}(t)\textbf{j} \) The derivative for a vector-valued function is itself a vector-valued function. Figure 12.2.1 shows that \(\textbf{r}^{\prime} (t) \) is a vector tangent to the curve given by \( \textbf{r} (t) \) and pointing in the direction where values for \(t\) increase.

Theorem 12.2.1 Differentiation of Vector-Valued Functions

1. If \( \textbf{r} (t) = f(t)\textbf{i} + g(t)\textbf{j} \), where \( f\) and \(g\) are differentiable functions for \(t\), then

\( \textbf{r} (t) = f^{\prime}(t)\textbf{i} + g^{\prime}(t)\textbf{j} \).    Two Dimensions

2. If \( \textbf{r} (t) = f(t)\textbf{i} + g(t)\textbf{j} + h(t)\textbf{k} \), where \( f\), \(g\), and \(h\) are differentiable functions for \(t\), then

\( \textbf{r}^{\prime}(t) = f^{\prime}(t)\textbf{i} + g^{\prime}(t)\textbf{j} + h^{\prime}(t)\textbf{k} \).    Three Dimensions

Example 12.2.1 Differentiating a Vector-Valued Function

Figure 12.2.2

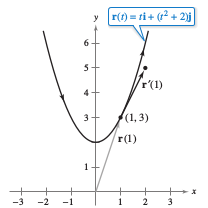
For the vector-valued function \( \textbf{r} (t) = t\textbf{i} + (t^{2}+2)\textbf{j} \) find \( \textbf{r}^{\prime} (t) \). Then sketch the plane curve represented by \( \textbf{r} (t) \) and the graph for \( \textbf{r} (1) \) and \( \textbf{r}^{\prime} (1) \). Solution Differentiate on a component-by-component basis to obtain \( \textbf{r}^{\prime} (t) = \textbf{i} + 2t\textbf{j} \). From the position vector \( \textbf{r} (t) \) the parametric equations are \(x=t\) and \(y=t^{2}+2\). The corresponding cartesian equation is \(y=x^{2}+2\). When \(t=1\), \( \textbf{r} (1)= \textbf{i} + 3\textbf{j} \) and \( \textbf{r}^{\prime} (1)= \textbf{i} + 2\textbf{j} \). Figure 12.2.2 shows \( \textbf{r} (1) \) drawn starting at the origin, and \( \textbf{r}^{\prime} (1) \) is drawn starting at the terminal point for \( \textbf{r} (1) \).

Example 12.2.2 Higher-Order Differentiation for Vector-Valued Function

For the vector-valued function

\( \textbf{r} (t) = \cos t\textbf{i} + \sin t\textbf{j} + 2 t \textbf{k} \)

find the following.
a.\( \textbf{r}^{\prime} (t) \)
b.\( \textbf{r}^{\prime \prime} (t) \)
c.\( \textbf{r}^{\prime} (t) \cdot \textbf{r}^{\prime \prime} (t) \)
d.\( \textbf{r}^{\prime}(t) \times \textbf{r}^{\prime \prime} (t) \)
Solution

a.\( \textbf{r}^{\prime} (t) \)	\(= -\sin t\textbf{i} + \cos t\textbf{j} + 2 \textbf{k} \:\:\:\: \)	First Derivative
b.\( \textbf{r}^{\prime \prime} (t) \)	\(= -\cos t\textbf{i} - \sin t\textbf{j} + 0 \textbf{k} \)
	\(= -\cos t\textbf{i} - \sin t\textbf{j} \)	Second Derivative
c.\( \textbf{r}^{\prime} (t) \cdot \textbf{r}^{\prime \prime} (t) \)	\(= \sin t \cos t - \sin t \cos t = 0 \)	Dot Product
	Note that the dot product is a real- valued function, not a vector- valued function.
d.\( \textbf{r}^{\prime}(t) \times \textbf{r}^{\prime \prime} (t) \)	$$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ -\sin t & \cos t & 2 \\ -\cos t & -\sin t & 0 \end{vmatrix} $$	Cross Product
	$$= \begin{vmatrix} \cos t & 2 \\ -\sin t & 0 \end{vmatrix}\textbf{i}-\begin{vmatrix}-\sin t & 2 \\ -\cos t & 0 \end{vmatrix}\textbf{j} $$	$$+\begin{vmatrix}-\sin t & \cos t \\ -\cos t & -\sin t \end{vmatrix}\textbf{k}$$
	\(= 2 \sin t \textbf{i} - 2 \cos t \textbf{j} + \textbf{k} \)

Example 12.2.3 Finding Intervals where a Curve is Smooth

The epicycloid is not smooth at the points where it intersects the axes. Figure 12.2.3

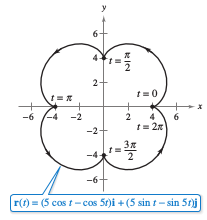
Find the intervals on which the epicycloid \(C\) given by \( \textbf{r} (t) = (5 \cos t - \cos 5t)\textbf{i} + (5 \sin t - \sin 5t)\textbf{j}, \: 0 \leqslant t \leqslant 2 \pi \) is smooth. Solution The parametrization for the curve represented by the vector-valued function \( \textbf{r}(t) = f(t)\textbf{i} + g(t)\textbf{j} + h(t)\textbf{k} \) is smooth on an open interval \(I\) when \(f^{\prime}\), \(g^{\prime}\), and \(h^{\prime}\) are continuous on \(I\) and \( \textbf{r}^{\prime}(t) \ne 0\) for any \(t\) value in the interval \(I\). The derivative for \( \textbf{r} \) is \( \textbf{r}^{\prime} (t) = (-5 \sin t + 5\sin 5t)\textbf{i} + (5 \cos t - 5\cos 5t)\textbf{j} \) In the interval \([0,2\pi]\), the only \(t\) values for which \( \textbf{r}^{\prime} (t) = 0\textbf{i} + 0\textbf{j} \) are \(t=0, \: \pi/2, \: \pi,\: 3\pi/2, \text{ and } 2\pi\). Therefore, the curve \(C\) is smooth on the intevals $$ \left( 0, \frac{\pi}{2}\right), \: \left( \frac{\pi}{2}, \pi\right), \: \left( \pi, \frac{3\pi}{2}\right) \text{, and } \left( \frac{3\pi}{2}, 2\pi\right) $$ and spiked at the cusps or nodes, where the curve changes direction, as shown in Figure 12.2.3.

Theorem 12.2.2 Vector-Valued Derivative Properties

Let \( \textbf{r} \) and \( \textbf{u} \) be differentiable vector-valued functions for \(t\), let \(w\) be a differentiable real-valued function for \(t\), and let \(c\) be a scalar.

$$\textbf{1. } \frac{d}{dt}[c\textbf{r}(t)]=c \textbf{r}^{\prime}(t) $$

$$\textbf{2. } \frac{d}{dt}[\textbf{r}(t) \pm \textbf{u}(t)]= \textbf{r}^{\prime} (t) \pm \textbf{u}^{\prime} (t)$$

$$\textbf{3. } \frac{d}{dt}[w(t)\textbf{r}(t)] = w(t)\textbf{r}^{\prime}(t) + w^{\prime}(t)\textbf{r}(t) $$

$$\textbf{4. } \frac{d}{dt}[\textbf{r}(t) \cdot \textbf{u}(t)]= \textbf{r}(t) \cdot \textbf{u}^{\prime}(t) + \textbf{r}^{\prime}(t) \cdot \textbf{u}(t) $$

$$\textbf{5. } \frac{d}{dt}[\textbf{r}(t) \times \textbf{u}(t)]= \textbf{r}(t) \times \textbf{u}^{\prime}(t) + \textbf{r}^{\prime}(t) \times \textbf{u}(t) $$

$$\textbf{6. } \frac{d}{dt}[\textbf{r}(w(t))]= \textbf{r}^{\prime}(w(t)) \textbf{w}^{\prime}(t)$$

$$\textbf{7. }\text{ If } \textbf{r}(t) \cdot \textbf{r}(t) =c \text{, then } \textbf{r}(t) \cdot \textbf{r}^{\prime}(t) =0.$$

Proof To prove Property 4, let

\( \textbf{r}(t) = f_{1}(t)\textbf{i} + g_{1}(t)\textbf{j} \text{ and } \textbf{u}(t) = f_{2}(t)\textbf{i} + g_{2}(t)\textbf{j} \)

where \( f_{1}, \: f_{2}, \: g_{1} \) and \( g_{2} \) are differentiable functions for \(t\). Then

\( \textbf{r}(t) \cdot \textbf{u}(t)= f_{1}(t)f_{2}(t) + g_{1}(t)g_{2}(t) \)

which produces

$$ \frac{d}{dt}[\textbf{r}(t) \cdot \textbf{u}(t)] $$	\(= f_{1}(t)f^{\prime}_{2}(t) + f_{1}^{\prime}(t)f_{2}(t) + g_{1}(t)g_{2}^{\prime}(t) + g_{1}^{\prime}(t)g_{2}(t) \)
	\(= [f_{1}(t)f_{2}^{\prime}(t) + g_{1}(t)g_{2}^{\prime}(t)] + [f_{1}^{\prime}(t)f_{2}(t) + g_{1}^{\prime}(t)g_{2}(t)] \)
	\(= \textbf{r}(t) \cdot \textbf{u}^{\prime}(t) + \textbf{r}^{\prime}(t) \cdot \textbf{u}(t) \)

Example 12.2.4 Using Derivative Properties

For

$$ \textbf{r}(t) = \frac{1}{t}\textbf{i} - \textbf{j} + \ln t \textbf{k} $$

and

\( \textbf{u}(t) = t^{2}\textbf{i} - 2 t \textbf{j} + \textbf{k} \),

find $$\textbf{a. }\frac{d}{dt}[\textbf{r}(t) \cdot \textbf{u}(t)] $$ $$\textbf{b. }\frac{d}{dt}[\textbf{u}(t) \times \textbf{u}^{\prime}(t)] $$ Solution
a. Because \( \textbf{r}^{\prime}(t) = -\frac{1}{t^{2}}\textbf{i} + \frac{1}{t} \textbf{k} \) and \( \textbf{u}^{\prime}(t) = 2t\textbf{i} - 2 \textbf{j} \) the derivative is

$$ \frac{d}{dt}[\textbf{r}(t) \cdot \textbf{u}(t)] $$	\(=\textbf{r}(t) \cdot \textbf{u}^{\prime}(t) + \textbf{r}^{\prime}(t) \cdot \textbf{u}(t) \)
	$$= \left( \frac{1}{t}\textbf{i} - \textbf{j} + \ln t \textbf{k} \right) \cdot (2t\textbf{i} - 2 \textbf{j}) + \left( -\frac{1}{t^{2}}\textbf{i} + \frac{1}{t} \textbf{k} \right) \cdot (t^{2}\textbf{i} - 2 t \textbf{j} + \textbf{k} ) $$
	\(=2+2+(-1)+ \frac{1}{t} \)
	\(=3+\frac{1}{t} \).

b. Because \( \textbf{u}^{\prime}(t) = 2t\textbf{i} - 2 \textbf{j} \) and \( \textbf{u}^{\prime \prime}(t) = 2\textbf{i} \), the derivative is

$$ \frac{d}{dt}[\textbf{u}(t) \times \textbf{u}^{\prime}(t)] $$	\(=[\textbf{u}(t) \times \textbf{u}^{\prime \prime}(t)] + [\textbf{u}^{\prime}(t) \times \textbf{u}^{\prime}(t)]\)
	$$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ t^{2} & -2t & 1 \\ 2 & 0 & 0 \end{vmatrix} + 0$$
	$$= \begin{vmatrix} -2 t & 1 \\ 0 & 0 \end{vmatrix}\textbf{i}-\begin{vmatrix} t^{2} & 1 \\ 2 & 0 \end{vmatrix}\textbf{j}+\begin{vmatrix} t^{2} & -2t \\ 2 & 0 \end{vmatrix}\textbf{k}$$
	\(= 0\textbf{i} - (-2)\textbf{j} + 4t\textbf{k}\)
	\(= 2\textbf{j} + 4t\textbf{k}\)

Integration Vector-Valued Functions

Definition 12.2.2 Vector-Valued Function Integration

1. If \( \textbf{r} (t) = f(t)\textbf{i} + g(t)\textbf{j} \), where \( f\) and \(g\) are continuous functions on \([a,b]\), then the indefinite integral, antiderivative, for \( \textbf{r} \) is

$$ \int \textbf{r} (t)\: dt = \left[ \int f(t)\:dt\right]\textbf{i} + \left[ \int g(t)\:dt\right]\textbf{j} \:\:\:\: \color{red}{ \text{Two dimensions}}$$

and its definite integral over the interval \( a \leqslant t \leqslant b \) is

$$ \int_{a}^{b} \textbf{r} (t)\: dt = \left[ \int_{a}^{b} f(t)\:dt\right]\textbf{i} + \left[ \int_{a}^{b} g(t)\:dt\right]\textbf{j}.$$

2. If \( \textbf{r} (t) = f(t)\textbf{i} + g(t)\textbf{j} + h(t)\textbf{k} \), where \( f\), \(g\), and \(h\) are continuous functions on \([a,b]\), then the indefinite integral, antiderivative, for \( \textbf{r} \) is

$$ \int \textbf{r} (t)\: dt = \left[ \int f(t)\:dt\right]\textbf{i} + \left[ \int g(t)\:dt\right]\textbf{j} + \left[ \int h(t)\:dt\right]\textbf{k} \:\:\:\: \color{red}{ \text{Three dimensions}}$$

and its definite integral over the interval \( a \leqslant t \leqslant b \) is

$$ \int_{a}^{b} \textbf{r} (t)\: dt = \left[ \int_{a}^{b} f(t)\:dt\right]\textbf{i} + \left[ \int_{a}^{b} g(t)\:dt\right]\textbf{j} + \left[ \int_{a}^{b} h(t)\:dt\right]\textbf{k}.$$

The indefinite integral for a vector-valued function, is a vector-valued function set with all differing by a constant vector \(C\). For example, if \( \textbf{r} (t) \) is a three-dimensional vector-valued function, then the indefinite integral \( \int \textbf{r} (t) \: dt \) yields three integration constants

$$ \int f(t) \: dt = F(t) +C_{1}, \: \int g(t) \: dt = G(t) +C_{2}, \: \int h(t) \: dt = H(t) +C_{3} \: $$

where \(F^{\prime}(t)=f(t), \: G^{\prime}(t)=g(t) \text{, and } H^{\prime}(t)=h(t) \). These three scalar constants produce one vector constant for integration.

$$ \int \textbf{r} (t)\: dt $$	\(= [F(t) + C_{1}]\textbf{i} +[ G(t) +C_{2}]\textbf{j} + [H(t) + C_{3}]\textbf{k} \)
	\(= [F(t)\textbf{i} + G(t)\textbf{j} + H(t)\textbf{k}] + [C_{1}\textbf{i} +C_{2}\textbf{j} + C_{3}\textbf{k}] \)
	\(= \textbf{R}(t)+ C \)

where \( \textbf{R}^{\prime}(t) = \textbf{r}(t). \)

Example 12.2.5 Integrating a Vector-Valued Function

Find the indefinite integral

$$ \int (t \textbf{i} + 3\textbf{j}) \: dt. $$

Solution Integrating on a component-by-component basis produces

$$ \int (t \textbf{i} + 3\textbf{j}) \: dt = \frac{t^{2}}{2}\textbf{i} +3t\textbf{j} + C.$$

Example 12.2.6 Definite Integral for a Vector-Valued Function

Evaluate the integral

$$ \int_{0}^{1} \textbf{r}(t) \: dt = \int_{0}^{1} \left( \sqrt[3]{t}\textbf{i} + \frac{1}{t+1}\textbf{j} + e^{-t}\textbf{k} \right) \: dt.$$

Solution

$$ \int_{0}^{1} \textbf{r}(t) \: dt $$	$$= \left( \int_{0}^{1} t^{1/3} \: dt \right)\textbf{i} + \left( \int_{0}^{1} \frac{1}{t+1} \: dt \right)\textbf{j} + \left( \int_{0}^{1} e^{-t} \: dt \right)\textbf{k}$$
	$$= \left[ \left( \frac{3}{4} \right) t^{4/3} \right]_{0}^{1} \textbf{i} + \left[\vphantom{\frac{3}{4} } \ln | t - 1 | \right]_{0}^{1} \textbf{j} + \left[ \vphantom{\frac{3}{4} } -e^{-t} \right]_{0}^{1} \textbf{k} $$
	$$= \frac{3}{4}\textbf{j} + ( \ln 2)\textbf{j} + \left( 1 - \frac{1}{e} \right)\textbf{k}$$

Example 12.2.7 The Antiderivative for a Vector-Valued Function

Find the antiderivative for

$$ \textbf{r}^{\prime}(t) = \cos 2t\textbf{j} -2 \sin t\textbf{j} + \frac{1}{1+t^{2}}\textbf{k}$$

that satisfies the initial condition

\( \textbf{r}(0) = 3\textbf{i} -2 \textbf{j} + \textbf{k} \)

Solution First step, find \( \textbf{r}(t) \).

\( \textbf{r}(t) \)	$$= \int \textbf{r}^{\prime}(t) \: dt $$
	$$= \left( \int \cos 2t \: dt \right)\textbf{i} + \left( \int -2 \sin t \: dt \right)\textbf{j} + \left( \int \frac{1}{1+t^{2}} \: dt \right)\textbf{k} $$
	$$= \left( \frac{1}{2} \sin 2t + C_{1} \right)\textbf{i} + \left( 2 \cos t + C_{2} \right)\textbf{j} + \left( \arctan t \right)\textbf{k} $$

As with real-valued functions, the antiderivative set for a vector-valued function \( \textbf{r}^{\prime} \) can be reduced to one by imposing an initial condition on the vector-valued function \( \textbf{r} \). Letting \( t=0 \) produces

\( \textbf{r}(0) \)	\(= (0+C_{1})\textbf{i} + (2+C_{2})\textbf{j} + (0+C_{3})\textbf{k} \)
\( 3\textbf{i} -2 \textbf{j} + \textbf{k} \)	\(= (0+C_{1})\textbf{i} + (2+C_{2})\textbf{j} + (0+C_{3})\textbf{k} \)

Equating corresponding components produces

\( C_{1}=3, \: 2 + C_{2}=-2, \: C_{3}=1.\)

The antiderivative that satisfies the initial condition is

$$ \textbf{r}(t) = \left( \frac{1}{2} \sin 2t + 3 \right)\textbf{i} + (2 \cos t -4)\textbf{j} + (\arctan t + 1)\textbf{k}. $$

Internal Links

Parent Article: Calculus III 12 Vector-Valued Functions