Calculus III 12.05 Arc Length and Curvature

Previous	Calculus III 12.04 Tangent Vectors and Normal Vectors
Next	Calculus III 13 Functions with Several Variables

12.5 Arc Length and Curvature

• Find the arc length for a three-dimensional curve.
• Use the arc length parameter to describe a two or three dimensional curve.
• Find the curvature for a curve at a point on the curve.
• Use a vector-valued function to find frictional force.

Arc Length

Section 10.3 describes the arc length for a smooth two dimensional curve \(C\) is given by the parametric equations \(x=x(t)\) and \(y=y(t)\), \(a \leqslant t \leqslant b\), is

$$s= \int_{a}^{b} \sqrt{[x^{\prime}(t)]^{2} + [y^{\prime}(t)]^{2} } \: dt.$$

In vector form, where \(C\) is described by \( \textbf{r}(t)=x(t)\textbf{i} + y(t)\textbf{j}\), the equation for arc length is expressed as

$$s= \int_{a}^{b} \| \textbf{r}^{\prime}(t) \| \: dt.$$

The formula for a two-dimensional curve's arc length has a natural extension to a smooth curve in three-dimensions, as stated in Theorem 12.5.1.

Theorem 12.5.1 Arc Length for a Three-Dimensional Curve

If \(C\) is a smooth curve given by \( \textbf{r}(t)=x(t)\textbf{i} + y(t)\textbf{j} + z(t)\textbf{k}\) on an interval \([a,b]\), then the arc length for \(C\) on the interval is

$$s= \int_{a}^{b} \sqrt{[x^{\prime}(t)]^{2} + [y^{\prime}(t)]^{2} + [z^{\prime}(t)]^{2} } \: dt = \int_{a}^{b} \| \textbf{r}^{\prime}(t) \| \: dt.$$

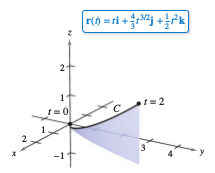
Example 12.5.1 Finding the Arc Length for a Curve in Three-Dimensions

As \(t\) increases from 0 to 2, the vector \( \textbf{r}(t) \) traces out a curve. Figure 12.5.1

Find the arc length for a curve given by $$ \textbf{r}(t) = t\textbf{i} + \frac{4}{3}t^{3/2}\textbf{j} + \frac{1}{2}t^{2}\textbf{k}$$ from \( t=0 \) to \( t=2 \), as shown in Figure 12.5.1. Solution Using \(x(t)=t\), \(y(t)=\frac{4}{3}t^{3/2}\), and \(z(t)=\frac{1}{2}t^{2}\) and differentiation produces \(x^{\prime}(t)=1\), \(y^{\prime}(t)=2t^{1/2}\), and \(z^{\prime}(t)=t\). The arc length from \(t=0\) to \(t=2\) is given by \(s\) $$= \int_{0}^{2} \sqrt{[x^{\prime}(t)]^{2} + [y^{\prime}(t)]^{2} + [z^{\prime}(t)]^{2} } \: dt \:\:\:\: \color{red}{ \text{Formula for arc length }} $$ $$= \int_{0}^{2} \sqrt{ 1 + 4t + t^{2} } \: dt $$ $$= \int_{0}^{2} \sqrt{ (t+2)^{2} -3 } \: dt $$ $$= \left[ \frac{t+2}{2} \sqrt{ (t+2)^{2} -3 } - \frac{3}{2} \ln |(t+2) + \sqrt{ (t+2)^{2} -3 } | \right]_{0}^{2} $$ $$= 2\sqrt{13} - \frac{3}{2} \ln (4+\sqrt{13} ) -1 + \frac{3}{2} \ln 3 \approx 4.816$$

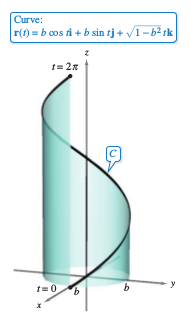
Example 12.5.2 Finding the Arc Length for a Helix

A helix with one turn. Figure 12.5.2

Find the length of one turn for the helix given by $$ \textbf{r}(t) = b \cos t\textbf{i} +b \sin t\textbf{j} + \sqrt{1-b^{2}} t\textbf{k}$$ as shown in Figure 12.5.2. Solution Begin by finding the derivative. $$ \textbf{r}^{\prime}(t) = -b \sin t\textbf{i} +b \cos t\textbf{j} + \sqrt{1-b^{2}} \textbf{k}$$ Applying Theorem 12.5.1 the arc length for one turn in the helix can be found by integrating \(\| \textbf{r}^{\prime}(t) \| \) from 0 to \( 2\pi \). \(s\) $$= \int_{0}^{2\pi} \| \textbf{r}^{\prime}(t) \| \: dt $$ $$= \int_{0}^{2 \pi} \sqrt{ b^{2}( \sin^{2} t + \cos^{2} t) + (1-b^{2}) } \: dt$$ $$= \int_{0}^{2 \pi} \: dt $$ $$= t \: {\Large ]_{0}^{2 \pi}} = 2\pi$$ The length is \( 2 \pi \) units.

Arc Length Parameter

Curves can be represented by vector-valued functions in different ways, depending on the parameter chosen. For motion along a curve, the convenient parameter is time \(t\). For studying the geometric properties for a curve, however, the convenient parameter is often arc length \(s\).

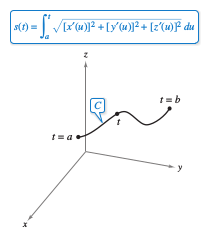
Definition 12.5.1 Arc Length Function

A helix with one turn. Figure 12.5.3

Let \(C\) be a smooth curve given by \( \textbf{r}(t) \) defined on the closed interval \([a,b]\). For \( a \leqslant t \leqslant \), the arc length function is $$s(t)= \int_{a}^{t} \sqrt{[x^{\prime}(u)]^{2} + [y^{\prime}(u)]^{2} + [z^{\prime}(u)]^{2} } \: du = \int_{a}^{t} \| \textbf{r}^{\prime}(u) \| \: du.$$ The arc length \(s\) is called the arc length parameter, as shown in Figure 12.5.3. Note that the arc length function \(s\) is nonnegative. It measures the distance along \(C\) from the initial point \((x(a),y(a),z(a))\) to the point \((x(t),y(t),z(t))\). Using Definition 12.5.1 Using the definition of the arc length function and the Second Fundamental Theorem of Calculus produces the derivative, $$ \frac{ds}{dt} = \| \textbf{r}^{\prime}(t)$$     Derivative for the Arc Length Function \( ds= \| \textbf{r}^{\prime}(t) \| \: dt.\)     In differential form.

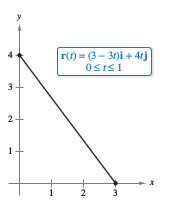
Example 12.5.3 Finding the Arc Length Function for a Line

The line segment from (3,0) to (0,4) can be parametrized using the arc length parameter \(s\). Figure 12.5.4

Find the arc length function \(s(t)\) for the line segment given by \( \textbf{r}(t) = (3-3t)\textbf{i} + 4t\textbf{j}, \: 0 \leqslant t \leqslant t \) and write \(\textbf{r}\) as a function for the parameter \(s\), as shown in Figure 12.5.4. Solution Differentiating produces \( \textbf{r}^{\prime}(t) \) \(= -3 \textbf{i} + 4\textbf{j} \) \( \| \textbf{r}^{\prime}(t) \| \) \(= \sqrt{ (-3)^{2} + 4^{2} } = 5 \) this produces \( s(t) \) $$= \int_{0}^{t} \| \textbf{r}^{\prime}(u) \| \: du $$ $$= \int_{0}^{t} 5 \: du $$ = \( 5t. \) Plugging \(s=5t\) or \(t=s/5\) into \( \textbf{r}(t) \) produces $$ \textbf{r}(s) = \left(3-\frac{3}{5}s \right)\textbf{i} + \frac{4}{5}s\textbf{j}, \: 0 \leqslant s \leqslant 5 $$ in \(s\) terms.

Expressing a vector-valued function in arc length parameter terms means that \( \| \textbf{r}^{\prime}(s) \| = 1 \). Using Example 12.5.3 would produce

$$\| \textbf{r}^{\prime}(s) \| = \sqrt{ \left(-\frac{3}{5} \right)^{2} + \left( \frac{4}{5} \right)^{2} } = 1. $$

For a smooth curve \(C\) represented by \( \textbf{r}(s) \) , where \(s\) is the arc length parameter, the arc length between \(a\) and \(b\) is

Arc Length	$$= \int_{a}^{b} \| \textbf{r}^{\prime}(s) \| \: ds $$
	$$= \int_{a}^{b} ds $$
	\(= b-a\)
	\(=\) interval length.

if \(t\) is any parameter such that \( \| \textbf{r}^{\prime}(s) \| = 1 \), then \(t\) must be the arc length parameter. These results are summarized in Theorem 12.5.2.

Theorem 12.5.2 Arc Length Parameter

If \(C\) is a smooth curve given by

\( \textbf{r}(t) = x(s)\textbf{i} + y(s)\textbf{j} \:\:\:\: \)Two-dimensional curve

or

\( \textbf{r}(t) = x(s)\textbf{i} + y(s)\textbf{j}+ z(s)\textbf{k} \:\:\:\: \)Three-dimensional curve

where \(s\) is the arc length parameter, then

\( \| \textbf{r}^{\prime}(s) \| = 1 \).

If \(t\) is any parameter for the vector-valued function \( \textbf{r} \) such that \( \| \textbf{r}^{\prime}(s) \| = 1 \), then \(t\) must be the arc length parameter.

Curvature

Curvature at \(P\) is greater than \(Q\). Figure 12.5.5 The curvature for a curve is the change rate's magnitude for \(T\) with respect to the arc length.. Figure 12.5.6

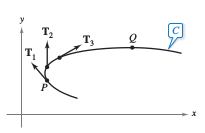
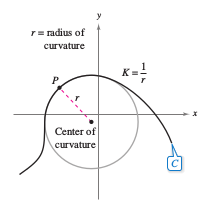
The arc length parameter is important in determining curvature — the measure for how sharply a curve bends. In Figure 12.5.5 the curve bends more sharply, or greater, at \(P\) than at \(Q\). Curvature is found by calculating the change rate magnitude for the unit tangent vector \( \textbf{T} \) with respect to the arc length \(s\), as shown in Figure 12.5.6. Definition 12.5.2 Curvature Let \(C\) be a smooth curve in two or three dimensions given by \( \textbf{r}(s) \), where \(s\) is the arc length parameter. The curvature \(K\) at \(s\) is $$ K= \left\| \frac{d \textbf{T} }{ds} \right\| = \| \textbf{T}^{\prime}(s) \|.$$ A circle has the same curvature at any point. The curvature and the radius for the circle are inversely related. That is, a circle with a large radius has a small curvature, and a circle with a small radius has a large curvature. This inverse relationship is made explicit in Example 12.5.4.

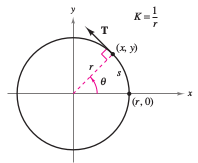
Example 12.5.4 Finding the Curvature for a Circle

The curvature for a circle is constant. Figure 12.5.7

Show that the curvature for a circle with radius \(r\) is $$ K=\frac{1}{r}.$$ Solution Let the circle be centered at the origin. Let \((x,y)\), as shown in Figure 12.5.7. By letting \(\theta\) be the central angle for the circle, it can be expressed as \( \textbf{r}(\theta) = r \cos \theta \textbf{i} +r \sin \theta \textbf{j} \:\:\:\: \)\(\theta\) is the parameter Applying Definition 12.5.2 yields \(s=r\theta\), the expression can be written in arc length parameter terms. $$ \textbf{r}(s) = r \cos \frac{s}{r} \textbf{i} +r \sin \frac{s}{r} \textbf{j} \:\:\:\: \color{red}{ \text{Arc length \(s\) is the parameter.}} $$ Differentiation produces $$ \textbf{r}^{\prime}(s) = - \sin \frac{s}{r} \textbf{i} + \cos \frac{s}{r} \textbf{j} $$ which reduces to \( \| \textbf{r}^{\prime}(s) \| = 1 \). \( \textbf{T}(s) \) $$= \frac{ \textbf{r}^{\prime}(s) }{\| \textbf{r}^{\prime}(s) \|} = - \sin \frac{s}{r} \textbf{i} + \cos \frac{s}{r} \textbf{j} $$ \( K \) $$= \| \textbf{T}^{\prime}(s) \| = \left \| - \frac{1}{r} \cos \frac{2}{r}\textbf{i} - \frac{1}{r} \sin \frac{2}{r}\textbf{j} \right \| = \frac{1}{r} \:\:\:\: $$ Curvature at any point on the circle.

Figure 12.5.8

A straight line has a curvature equal to zero. Try checking this by finding the curvature for the line given by $$ \textbf{r}(s) = \left(3- \frac{3}{5}s \right) \textbf{i} +r \frac{4}{5} s\textbf{j}. $$ Example 12.5.4 found the curvature by applying Definition 12.5.2 directly. This requires writing the curve in the arc length parameter term \(s\). Theorem 12.5.3 provides two formulas for finding a curve's curvature using an arbitrary parameter \(t\). Proving this is left as an exercise. Theorem 12.5.2 Formulas for Curvature If \(C\) is a smooth curve given by \( \textbf{r}(t) \), then the curvature \(K\) for \(C\) at \(t\) is described by the properties below. 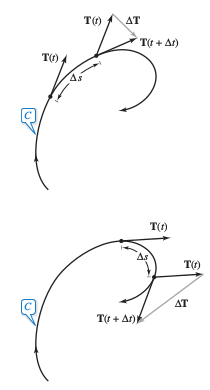\(K\) $$= \frac{ \| \textbf{T}^{\prime}(t) \| }{ \| \textbf{r}^{\prime}(t) \| } \:\:\:\: $$ Property 1 $$= \frac{ \| \textbf{r}^{\prime}(t) \times \textbf{r}^{\prime \prime}(t) \| }{ \| \textbf{r}^{\prime}(t) \|^{3} } \:\:\:\: $$ Property 2 Because \( \| \textbf{r}^{\prime}(t) \| = ds/dt \), Property 1 states that the curvature is the ratio with the change rate for the norm tangent vector, \( \| \textbf{T}^{\prime}(t) \| \), over the norm arc length change rate \(\| \textbf{r}^{\prime}(t) \| \). For a simple proof, let \( \Delta t\) be an arbitrary number that is arbitrarily "small". Then, $$ \frac{ \textbf{T}^{\prime}(t) }{ \frac{ ds}{dt} } \approx \frac{ \frac{ [\textbf{T}(t+\Delta t) - \textbf{T}(t)] }{\Delta t} }{ \frac{ [s(t+\Delta t) - s(t)] }{\Delta t} } = \frac{ \textbf{T}(t+\Delta t) - \textbf{T}(t) }{ s(t+\Delta t) - s(t)} = \frac{ \Delta \textbf{T} }{ \Delta s}. $$ For any given \( \Delta s\), the greater the length for \( \Delta \textbf{T} \), the more the curve bends at \(t\), as shown in Figure 12.5.8.

Example 12.5.5 Finding the Curvature for a Three Dimensional Curve

Find the curvature for the curve given by

$$ \textbf{r}(t) = 2t \textbf{i} + t^{2} \textbf{j} - \frac{1}{3}t^{3} \textbf{k}. $$

Solution It is not apparent whether this parameter represents the arc length. Use Theorem 12.5.2 Property 1 to find out.

\( \textbf{r}^{\prime}(t) \)	\(= 2 \textbf{i} + 2t \textbf{j} - t^{2} \textbf{k} \)
\( \textbf{r}^{\prime}(t) \)	\(= \sqrt{ 4 + 4t^{2} + t^{4} } \:\:\:\: \)	Length for \( \textbf{r}^{\prime}(t) \)
	\(=t^{2} + 2 \)
\( \textbf{T}(t) \)	$$= \frac{ \textbf{r}^{\prime}(t) }{ \| \textbf{r}^{\prime}(t) \| } $$
	$$= \frac{ 2 \textbf{i} + 2t \textbf{j} - t^{2} \textbf{k} }{ t^{2} + 2} $$
\( \textbf{T}^{\prime}(t) \)	$$= \frac{ (t^{2} + 2)(2 \textbf{j} - 2t \textbf{k})-(2t)( 2 \textbf{i} + 2t \textbf{j} - t^{2} \textbf{k} ) }{ (t^{2} + 2)^{2} }$$
	$$= \frac{ -4t\textbf{i} + (4-2 t^{2})\textbf{j} - 4t \textbf{k} }{ (t^{2} + 2)^{2} } $$
\( \| \textbf{T}^{\prime}(t) \| \)	$$= \frac{ \sqrt{ 16t^{2}+16-16t^{2}+4t^{4}+16t^{2} }}{ (t^{2} + 2)^{2} } $$
	$$= \frac{ 2(t^{2} + 2) }{ (t^{2} + 2)^{2} }$$
	$$= \frac{ 2 }{ t^{2} + 2 } $$	Length for \( \textbf{T}^{\prime}(t) \)

Therefore,

$$ K = \frac{ \| \textbf{T}^{\prime}(t) \| }{ \| \textbf{r}^{\prime}(t) \| } = \frac{ 2 }{ (t^{2} + 2)^{2} } \:\:\:\: \color{red}{ \text{ Curvature }}$$

Theorem 12.5.3 Curvature in Cartesian Coordinates

Circular curvature. Figure 12.5.9

If \(C\) is the graph for a twice-differentiable function given by \(y=f(x)\), then the curvature \(K\) at the point \((x,y)\) is $$ K = \frac{ |y^{\prime \prime}| }{ \left[ 1+ (y^{\prime})^{2} \right]^{3/2} }.$$ Proof By representing the curve \(C\) by \( \textbf{r}(t) = x \textbf{i} + f(x) \textbf{j} + 0 \textbf{k} \), where \(x\) is the parameter, the derivatives are simplified to \( \textbf{r}^{\prime }(x) \) \(= \textbf{i} + f(x)^{\prime} \textbf{j} \) First derivative \( \| \textbf{r}^{\prime }(x) \| \) \(= \sqrt { 1 + [f(x)^{\prime}]^{2}} \:\:\:\: \) First derivative, normalized \( \textbf{r}^{\prime \prime }(x) \) \(= f(x)^{\prime \prime} \textbf{j} \) Second derivative Because \( \textbf{r}^{\prime }(x) \times \textbf{r}^{\prime \prime }(x) = f^{\prime \prime }(x)\textbf{k}\), it follows that the curvature is \(K\) $$= \frac{ \| \textbf{r}^{\prime}(t) \times \textbf{r}^{\prime \prime}(t) \| }{ \| \textbf{r}^{\prime}(t) \|^{3} } $$ $$= \frac{ | f^{\prime \prime }(x) | }{ \left \{ 1 + [f^{\prime}(x)]^{2} \right \}^{3/2} } $$ $$= \frac{ | y^{\prime \prime } | }{ \left[ 1 + ( y^{\prime})^{2} \right]^{3/2} }. $$ Let \(C\) be a curve with curvature \(K\) at point \(P\). The circle passing through point \(P\) with radius \(r=1/K\) is called the circle of curvature when the circle lies on the curve's concave side and shares a common tangent line with the curve at point \(P\). The radius is called the radius of curvature at point \(P\), and the circle's center is called the center of curvature. The circle of curvature provides a nice way to estimate the curvature \(K\) at a point \(P\) on a curve graphically. Using a compass, sketch a circle that lies against the curve's concave side at point \(P\), as shown in Figure 12.5.9. If the circle has a radius \(r\), then the curvature is estimated as \(K=1/r\).

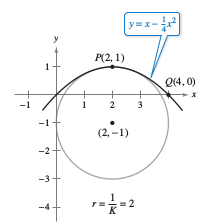
Example 12.5.6 Finding Curvature in Cartesian Coordinates

Curvature circle. Figure 12.5.10

Find the curvature for the parabola given by $$ y = x - \frac{1 }{ 4} x^{2} \text{, at }x=2.$$ Then sketch the curvature circle at (2,1). Solution Applying Theorem 12.5.3 at \(x=2\) produces \( y^{\prime} \) $$= 1 - \frac{x}{2} $$ \(= 0\) \( y^{\prime \prime} \) $$= - \frac{1}{2}$$ \(K\) $$= \frac{ | y^{\prime \prime } | }{ \left[ 1 + ( y^{\prime})^{2} \right]^{3/2}} = \frac{1}{2} $$ Because the curvature at \(P(2,1)\) is \(1/2\), the radius for the curvature circle at \(P\) is 2. The curvature center is (2,1), as shown in Figure 12.5.10. Note in Figure 12.5.10 the greatest curvature is at \(P\). Try showing the curvature at \(Q(4,0)\) is \(1/2^{5/2} \approx 0.177\).

The thrust felt by passengers in a car going around a turn depends on two variables - The car's speed and how sharp the turn is. Figure 12.5.11

Arc length and curvature are closely related to the tangential and normal acceleration components. The tangential acceleration component is the change rate for the speed, which in turn is the change rate for the arc length. It is negative as a moving object slows down and positive as it speeds up. The tangential component is solely a function for the arc length and is curvature independent. The normal acceleration component, in contrast, depends on both speed and curvature. It measures the acceleration acting perpendicular to the motion direction. To see why the normal component is affected by both speed and curvature, imagine a car driving around a turn, as shown in Figure 12.5.11. When the speed is high and the turn is sharp, you feel yourself thrown against the car door. By lowering the speed or taking a more gentle turn, the sideways thrust lessens. Theorem 12.5.4 explicitly states the relationships among speed, curvature, and the acceleration components.

Theorem 12.5.4 Acceleration, Speed, and Curvature

If \( \textbf{r}(t) \) is the position vector for a smooth curve \(C\), then the acceleration vector is given by

$$ \textbf{a}(t) = \frac{ d^{2}s}{dt^{2}}\textbf{T} + K \left( \frac{ ds}{dt} \right)^{2}\textbf{N} $$

where \(K\) is the curvature for \(C\) and \(ds/dt\) is the speed.
Proof For the position vector \( \textbf{r}(t) \), the acceleration vector is

\( \textbf{a}(t) \)	$$= a_{\textbf{T}}\textbf{T} + a_{\textbf{N}}\textbf{N} $$
	$$= \frac{ ds}{dt}[ \| \textbf{v} \| ]\textbf{T} + \| \textbf{v} \| \|\textbf{T}^{\prime} \| \textbf{N}$$
	$$= \frac{ d^{2}s}{dt^{2}}\textbf{T} + \frac{ ds}{dt} \left( \| \textbf{v} \|K \right) \textbf{N} $$
	$$= \frac{ d^{2}s}{dt^{2}}\textbf{T} + K\left( \frac{ ds}{dt} \right)^{2} \textbf{N}. $$

Example 12.5.7 Tangential and Normal Components of Acceleration

Find \( a_{\textbf{T}} \) and \( a_{\textbf{N}} \) for the curve given by

$$ \textbf{r}(t) = 2t\textbf{i} + t^{2}\textbf{j} - \frac{1}{3}t^{3}\textbf{k}. $$

Solution Example 12.5.5 proved that

$$ \frac{ ds}{dt} = \| \textbf{r}^{\prime}(t) \| = t^{2}+2 \text{ and }K= \frac{2}{(t^{2}+2)^{2}}.$$

Therefore,

\( a_{\textbf{T}} \)	$$ = \frac{ d^{2}s}{dt^{2}} = 2t \:\:\:\:$$	Tangential component
and
\( a_{\textbf{N}} \)	$$ = K\left( \frac{ ds}{dt} \right)^{2} = \frac{2}{(t^{2}+2)^{2}}(t^{2}+2)^{2} = 2 \:\:\:\: $$	Normal component

Application

There are many applications in physics and engineering dynamics that involve the relationships among speed, arc length, curvature, and acceleration. One such application concerns frictional force.

A moving object with mass \(m\) is in contact with a stationary object. The total force required to produce an acceleration \( \textbf{a} \) along a given path is

\( \textbf{F} \)	\(= m\textbf{a} \)
	$$= m \frac{d^{2}s}{dt^{2}}\textbf{T} + mK \left( \frac{ds}{dt} \right)^{2}\textbf{N}$$
	$$= ma_{\textbf{T}}\textbf{T} + ma_{\textbf{N}}\textbf{N}.$$

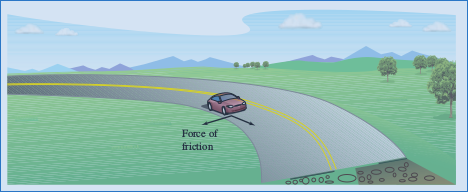
The stationary object supplies the force of friction toward the total force. For example, when a car moving with constant speed is rounding a turn, the roadway exerts a frictional force that keeps the car from sliding off the road. If the car is not sliding, the frictional force is perpendicular to the motion direction and has a magnitude equal to the normal acceleration component, as shown in Figure 12.5.12. The potential frictional force for a road around a turn can be increased by banking the roadway, as at a racetrack.

Frictional force exerts pressure perpendicular to the motion.
Figure 12.5.12

Example 12.5.8 Frictional Force

Figure 12.5.13

A 360-kilogram go-cart is driven at 60 kilometers per hour around a circular racetrack with a 12 meter radius, as shown in Figure 12.5.13. To keep the cart from skidding off course, what frictional force must the track surface exert on the tires? Solution The frictional force must equal the mass times the normal acceleration component. For this circular path, the curvature is $$ K = \frac{1}{12} \:\:\:\: \color{red}{ \text{ Curvature for a circular racetrack }}$$ Therefore, the frictional force is \( ma_{\textbf{T}} \) $$= mK \left( \frac{ds}{dt} \right)^{2} $$ $$= (360\text{ kg}) \left( \frac{1}{12\text{ m}} \right) \left( \frac{60,000\text{ m} }{3600\text{ sec}} \right)^{2}$$ \( \approx 8333 (\text{kg})(\text{m})/(\text{sec})^{2}\)

Internal Links

Parent Article: Calculus III 12 Vector-Valued Functions