Calculus III 13.03 Partial Derivatives

Previous	Calculus III 13.02 Limits and Continuity
Next	Calculus III 13.04 Differentials

13.03 Partial Derivatives

• Find and use partial derivatives for a function with two variables.
• Find and use partial derivatives for a function with three or more variables.
• Find higher-order partial derivatives for a function with two or three variables.

Partial Derivatives for a Function with Two Variables

In functions with several variables many applications require changing one variable while holding the others constant. This process is called partial differentiation, and the result is referred to as the partial derivative for \(f\) with respect to the chosen independent variable.

Definition 13.3.1 Partial Derivatives for a Function with Two Variables

If \(z=f(x,y)\), then the first partial derivatives for \(f\) with respect to \(x\) and \(y\) are the functions \(f_{x}\) defined by

$$ f_{x}(x,y) = \lim_{\Delta x \rightarrow 0} \frac{ f(x+\Delta, y) - f(x,y) }{ \Delta x} \:\:\:\: \color{red}{ \text{Partial derivative with respect to }x}$$

and

$$ f_{y}(x,y) = \lim_{\Delta y \rightarrow 0} \frac{ f(x+\Delta, y) - f(x,y) }{ \Delta y} \:\:\:\: \color{red}{ \text{Partial derivative with respect to }y}$$

provided the limits exist.

If \(z=f(x,y)\), then to find \(f_{x}\) consider \(y\) constant and differentiate with respect to \(x\). To find \(f_{y}\) consider \(x\) constant and differentiate with respect to \(y\). This can be extended to function with three or more variables.

Example 13.3.1 Finding Partial Derivatives

a. To find \(f_{x}\) for \(f(x,y) = 3x-x^{2}y^{2}+ 2x^{3}y\), consider \(y\) a constant and differentiate with respect to \(x\).

\( f_{x}(x,y) = 3 - 2xy^{2} + 6x^{2}y \:\:\:\: \)Partial derivative with respect to \(x\)

To find \(f_{y}\) , consider \(x\) a constant and differentiate with respect to \(y\).

\( f_{y}(x,y) = -2x^{2}y + 2x^{3} \:\:\:\: \)Partial derivative with respect to \(y\)

b. To find \(f_{x}\) for \(f(x,y) = (\ln x)(\sin x^{2}y)\), consider \(y\) a constant and differentiate with respect to \(x\).

\( f_{x}(x,y) = (\ln x)(\cos x^{2}y)(2xy) + \frac{\sin x^{2}y}{x} \:\:\:\: \)Partial derivative with respect to \(x\)

To find \(f_{y}\) , consider \(x\) a constant and differentiate with respect to \(y\).

\( f_{y}(x,y) = (\ln x)(\cos x^{2}y)(x^{2}) + \frac{\sin x^{2}y}{x} \:\:\:\: \)Partial derivative with respect to \(y\)

Definition 13.3.1 Notation for First Partial Derivatives

For \(z=f(x,y)\), the partial derivatives \(f_{x}\) and \(f_{y}\) are denoted by

$$ \frac{\partial }{\partial x} f(x,y) = f_{x}(x,y) = z_{x} = \frac{\partial z}{\partial x} \:\:\:\: \color{red}{ \text{Partial derivative with respect to } x}$$

and

$$ \frac{\partial }{\partial y} f(x,y) = f_{y}(x,y) = z_{y} = \frac{\partial z}{\partial y} \:\:\:\: \color{red}{ \text{Partial derivative with respect to } y}$$

The first partials evaluated at the point \((a,b)\) are denoted by

$$ \left. \frac{\partial z}{\partial x}\right|_{(a,b)} = f_{x}(a,b) $$

and

$$ \left. \frac{\partial z}{\partial y}\right|_{(a,b)} = f_{y}(a,b) $$

where \( \partial \) stands for partial derivative.

Example 13.3.2 Finding and Evaluating Partial Derivatives

Figure 13.3.1

For \( f(x,y) = xe^{x^{2}y} \) find \( f_{x} \) and \( f_{y} \), and evaluate each at the point \( (1,\ln 2)\). Solution For \( f_{x} \), take the first partial derivative with respect to \( x \). \( f_{x}(x,y) = xe^{x^{2}y}(2xy) + e^{x^{2}y} \:\:\:\: \)Partial derivative with respect to \(x\) Evaluate it at \( (1,\ln 2)\). \( f_{x}(1,\ln 2) \) \(= e^{\ln 2}(2 \ln 2) + e^{\ln 2} \) \(= 4 \ln 2 + 2\) For \( f_{y} \), take the first partial derivative with respect to \( y \). \( f_{y}(x,y) \) \( = xe^{x^{2}y}(x^{2}) \) \( = x^{3} e^{x^{2}y} \:\:\:\: \) Partial derivative with respect to \(y\) Evaluate it at \( (1,\ln 2)\). \( f_{y}(1,\ln 2) \) \(= e^{\ln 2} \) \(= 2.\)

Figure 13.3.2

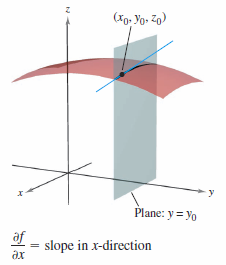
The partial derivatives for a function with two variables, \( z = f(x,y) \), have a useful geometric interpretation. If \( y = y_{0} \), then \( z= f(x,y_{0})\) represents the curve formed by intersecting the surface \( z = f(x,y) \) with the plane \( y = y_{0} \), as shown in Figure 13.3.1. Therefore, $$f_{x}(x_{0},y_{0}) = \lim_{\Delta x \rightarrow 0} \frac{ f(x_{0} + \Delta x,y_{0})-f(x_{0},y_{0})}{\Delta x} $$ represents the slope for the curve at the point \((x_{0},y_{0},f(x_{0},y_{0}))\). Note that both the curve and the tangent line lie in the plane \( y = y_{0} \). 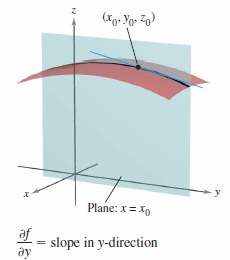Similarly, $$f_{y}(x_{0},y_{0}) = \lim_{\Delta y \rightarrow 0} \frac{ f(x_{0},y_{0}+ \Delta y)-f(x_{0},y_{0})}{\Delta y} $$ represents the slope for the curve given by the intersection between \( z = f(x,y) \) and the plane \( x = x_{0}\) at \((x_{0},y_{0},f(x_{0},y_{0}))\), as shown in Figure 13.3.2. The values \( \partial f/ \partial x\) and \( \partial f/ \partial y \) at the point \((x_{0},y_{0},z_{0})\) denote the slopes of the surface in the \(x\)- and \(y\)- directions, respectively.

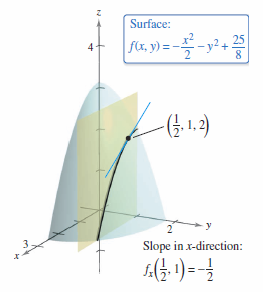
Example 13.3.3 Finding the Slopes for a Surface

Find the slopes in the \(x\) and \(y\) directions for the surface

$$ f(x,y) = -\frac{x^{2}}{2} - y^{2} + \frac{25}{8} $$

at the point

$$ \left( \frac{1}{2}, 1,2 \right).$$

Solution The partial derivatives for \(f\) with respect to \(x\) and \(y\) are

\( f_{x}(x,y) = -x \) and \(f_{y}(x,y) = -2y \).

The slope in the \(x\)-direction is

$$ f_{x} \left( \frac{1}{2}, 1,2 \right) = -\frac{1}{2} \:\:\:\: \color{red}{ \text{Figure 13.3.3 }}$$

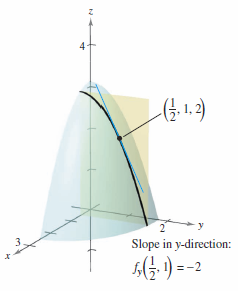
The slope in the \(y\)-direction is

$$ f_{y} \left( \frac{1}{2}, 1,2 \right) = -2. \:\:\:\: \color{red}{ \text{Figure 13.3.4 }}$$

Figure 13.3.3

Figure 13.3.4

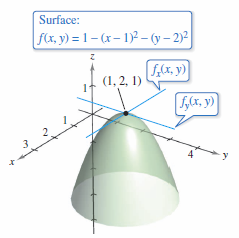
Example 13.3.4 Finding the Slopes for a Surface at a Point

Figure 13.3.5

Find the slope for the surface \( f(x,y) = 1 - (x-1)^{2}-(y-2)^{2} \) at the point \((1,2,1)\) in the \(x\) and \(y\) directions. Solution The partial derivatives for \(f\) with respect to \(x\) and \(y\) are \( f_{x}(x,y) = -2(x-1) \) and \(f_{y}(x,y) = -2(y-2) \). The slope in the \(x\)-direction at the point \((1,2,1)\) is \( f_{x} ( \color{red}{1},\color{red}{2} ) = -2(\color{red}{1}-1) = 0 \) The slope in the \(y\)-direction at the point \((1,2,1)\) is \( f_{y} ( \color{red}{1},\color{red}{2} ) = -2(\color{red}{2}-2) = 0 \) as shown in Figure 13.3.5.

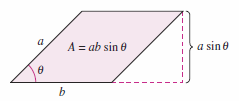
Example 13.3.5 Using Partial Derivatives to Find A Change Rate

The parallelogram's area is \(ab \sin \theta\) Figure 13.3.6

The area for a parallelogram with adjacent sides \(a\) and \(b\) and the included angle \(\theta\) is given by \(A=ab \sin \theta\), as shown in Figure 13.3.6. a. Find the change rate for \(A\) with respect to \(a\) for \(a=10\), \(b=20\), and \( \theta = \pi /6\). b. Find the change rate for \(A\) with respect to \(\theta\) for \(a=10\), \(b=20\), and \( \theta = \pi /6\). Solution a. To find the change rate for the area with respect to \(a\), hold \(b\) and \(\theta\) constant and differentiate with respect to \(a\) to produce $$ \frac{\partial A}{\partial a} = b \sin \theta \:\:\:\: \color{red}{ \text{Find partial derivative with respect to }a}$$ For \(a=10\), \(b=20\), and \( \theta = \pi /6\), the change rate for the area with respect to \(a\) is $$ \frac{\partial A}{\partial a} = 20 \sin \frac{\pi}{6} = 10 \:\:\:\: \color{red}{ \text{Substitute for } b \text{ and } \theta.}$$ b. To find the change rate for the area with respect to \(\theta\), hold \(a\) and \(b\) constant and differentiate with respect to \(\theta\) to produce $$ \frac{\partial A}{\partial \theta } = ab \cos \theta \:\:\:\: \color{red}{ \text{Find partial derivative with respect to }\theta}$$ For \(a=10\), \(b=20\), and \( \theta = \pi /6\), the change rate for the area with respect to \(\theta\) is $$ \frac{\partial A}{\partial \theta} = 200 \cos \frac{\pi}{6} = 100\sqrt{3} \:\:\:\: \color{red}{ \text{Substitute for }a, \: b \text{ and } \theta.}$$

Partial Derivatives for a Function with Three or More Variables

Partial derivatives naturally extend to functions with three or more variables. If \(w=f(x,y,x)\), there are three partial derivatives, each formed by holding the other two constant. To define the partial derivative for \(w\) with respect to \(x\), consider \(y\) and \(z\) constants and differentiate only with respect to \(x\). Repeat the process but change the variable when finding derivatives for \(w\) with respect to \(y\), \(z\), or any higher variable.

$$ \frac{\partial w}{\partial x} $$	$$= f_{x}(x,y,z) $$	$$= \lim_{\Delta x \rightarrow 0} \frac{ f(x+ \Delta x,y,z) - f(x,y,z)}{\Delta x} $$
$$ \frac{\partial w}{\partial y} $$	$$= f_{y}(x,y,z) $$	$$= \lim_{\Delta y \rightarrow 0} \frac{ f(x,y+ \Delta y,z) - f(x,y,z)}{\Delta y} $$
$$ \frac{\partial w}{\partial z} $$	$$= f_{z}(x,y,z) $$	$$= \lim_{\Delta x \rightarrow 0} \frac{ f(x,y,z + \Delta z) - f(x,y,z)}{\Delta z} $$

In general, if \(w=f(x_{1},x_{2},...,x_{n})\), then there are \(n\) partial derivatives denoted by

$$ \frac{\partial w}{\partial x_{k}} = f_{x_{k}}(x_{1},x_{2},...,x_{n}), \: k=1,2,...,n. $$

To find the partial derivative with respect to a variable, hold the other variables constant and differentiate with respect to the given variable.

Example 13.3.6 Finding Partial Derivatives Among Three Variables

a. To find the partial derivative for \(f(x,y,x) = xy+yz^{2}+xz \) with respect to \(z\), consider \(x\) and \(y\) constants.

$$ \frac{\partial}{\partial z} [xy+yz^{2}+xz] = 2yz + x.$$

b. To find the partial derivative for \(f(x,y,x) = z \sin(xy^{2}+2z) \) with respect to \(z\), consider \(x\) and \(y\) constants. Using the Product Rule produces.

$$ \frac{\partial w}{\partial z} [z \sin (xy^{2}+2z)]$$	$$=(z) \frac{\partial w}{\partial z}[\sin (xy^{2}+2z)] + \sin (xy^{2}+2z)\frac{\partial w}{\partial z} [z] $$
	$$= (z) [\cos (xy^{2}+2z)](2) + \sin (xy^{2}+2z) $$
	$$= 2z [\cos (xy^{2}+2z)] + \sin (xy^{2}+2z) $$

c. To find the partial derivative for

$$ f(x,y,z,w)= \frac{x+y+z}{w} $$

with respect to \(w\), consider \(x\), \(y\), and \(z\) as constants. This produces

$$ \frac{\partial }{\partial w} \left[ \frac{x+y+z}{w} \right] = \frac{x+y+z}{w^{2}} $$

Higher-Order Partial Derivatives

Second, third, and higher-order partial derivatives for a function with several variables can be found, provided such derivatives exist. Higher-order derivatives are denoted by the order in which the differentiation occurs. For instance, the function \(z=f(x,y)\) has the following second partial derivatives.
1. Differentiate twice with respect to \(x\):

$$ \frac{\partial }{\partial x} \left( \frac{\partial f}{\partial x} \right) = \frac{\partial^{2} f}{\partial x^{2}} =f_{xx} $$

2. Differentiate twice with respect to \(y\):

$$ \frac{\partial }{\partial y} \left( \frac{\partial f}{\partial y} \right) = \frac{\partial^{2} f}{\partial y^{2}} =f_{yy} $$

3. Differentiate first with respect to \(x\) and then with respect to \(y\):

$$ \frac{\partial }{\partial y} \left( \frac{\partial f}{\partial x} \right) = \frac{\partial^{2} f}{ \partial y \partial x} =f_{xy} $$

4. Differentiate first with respect to \(y\) and then with respect to \(x\):

$$ \frac{\partial }{\partial x} \left( \frac{\partial f}{\partial y} \right) = \frac{\partial^{2} f}{ \partial x \partial y} =f_{yx} $$

The third and fourth cases are called mixed partial derivatives.

Example 13.3.7 Finding Second Partial Derivatives

Find the second partial derivatives for

\( f(x,y) = 3xy^{2} - 2y + 5x^{2}y^{2} \)

and determine the value for \( f_{xy}(-1,2)\).
Solution Begin by finding the first partial derivatives with respect to \(x\) and \(y\).

\( f_{x}(x,y) = 3y^{2} + 10xy^{2} \) and \(f_{y}(x,y) = 6xy + 10x^{2}y \)

Differentiate each with respect to \(x\) and \(y\).

\( f_{xx}(x,y) \)	\(= 10y^{2} \)	and	\( f_{yy}(x,y) \)	\(= 6x+ 10x^{2} \)
\( f_{xy}(x,y) \)	\(= 6y + 20xy \)	and	\( f_{yx}(x,y) \)	\(= 6y + 20xy \)

At \((-1,2)\), the value for \( f_{xy} \) is

\( f_{xy}(-1,2) = 12-40=-28 \).

Notice the two mixed partials are equal. This is described in Theorem 13.3.1.

Theorem 13.3.1 Mixed Partial Derivative Equality

If \(f\) is a function for \(x\) and \(y\) such that \( f_{xy} \) and \( f_{yx}\) are continuous on an open disk \(R\), then, for every \((x,y)\) in \(R\),

\( f_{xy}(x,y) = f_{yx}(x,y) \).

This also applies to a function \(f\) with three or more variables so long as all second partial derivatives are continuous. For example, if

\( w = f(x,y,z) \:\:\:\: \)Function with three variables

and all the second partial derivatives are continuous in an open region \(R\), then at each point in \(R\), the order for differentiation in the mixed second partial derivatives is irrelevant. If the third partial derivatives for \(f\) are also continuous, then the order for differentiation for the mixed third partial derivatives is irrelevant.

Example 13.3.8 Finding Higher-Order Partial Derivatives

Show that \( f_{xz} = f_{zx} \) and \( f_{xzz} = f_{zxz} = f_{zzx} \) for the function

\( f(x,y,z) = ye^{x} + x \ln z\).

Solution
First partials:

\( f_{x}(x,y,z) = ye^{x} + \ln z\), \( f_{z}(x,y,z) = x/z\)

Second partials. Note the first two are equal:

\( f_{xz}(x,y,z) = 1/z\), \( f_{zx}(x,y,z) = 1/z\), \( f_{zz}(x,y,z) = -x/z^{2} \)

Third partials. Note that all three are equal:

\( f_{xzz}(x,y,z) = -1/z^{2}\), \( f_{zxz}(x,y,z) = -1/z^{2}\), \( f_{zzx}(x,y,z) = -1/z^{2} \)

Internal Links

Parent Article: Calculus III 13 Functions with Several Variables