Calculus III 13.04 Differentials

Previous	Calculus III 13.03 Partial Derivatives
Next	Calculus III 13.05 Chain Rules for Functions with Several Variables

13.04 Differentials

• Increments and differentials.
• Extend differentiability to a function with two variables.
• Use a differential as an approximation.

Increments and Differentials

In this discussion increments and differentials are generalized to functions with two or more variables. Recall from Section 3.9 that for \(y=f(x)\), the differential for \(y\) was defined as

\( dy = f^{\prime}(x) \: dx \).

Similar terminology is used for a function with two variables, \(z=f(x,y)\). Consider \(\Delta x\) and \(\Delta y\) are the increments for \(x\) and \(y\), and the increment for \(z\) is

\(\Delta z = f(x+\Delta x, y + \Delta y) - f(x,y). \:\:\:\: \)Increment for \(z\)

Definition 13.4.1 Total Differential

If \(z=f(x,y)\) and \(\Delta x\) and \(\Delta y\) are the increments for \(x\) and \(y\), then the differentials for the independent variables \(x\) and \(y\) are

\( dx = \Delta x \text{ and } dy=\Delta y \)

and the total differential for the dependent variable \(z\) is

$$ dz = \frac{\partial z}{\partial x}\: dx + \frac{\partial z}{\partial y}\: dy = f_{x}(x,y)\: dx + f_{y}(x,y) \:dy.$$

This can be extended to functions with three or more variables. For instance, if \(w=f(x,y,z,u)\), then \(dx=\Delta x\), \(dy=\Delta y\), \(dz=\Delta z\), and \(du=\Delta u\) then the total differential for \(w\) is

$$ dw = \frac{\partial w}{\partial x} \:dx + \frac{\partial w}{\partial y} \:dy + \frac{\partial w}{\partial z} \:dz + \frac{\partial w}{\partial u} \:du.$$

Example 13.4.1 Finding the Total Differential

Find the total differential for each function
a. \( z=2x \sin y - 3x^{2}y^{2}\)
b. \( w=x^{2} + y^{2} + z^{2} \)
Solution
a. The total differential \(dz\) for \(z=2x \sin y - 3x^{2}y^{2}\) is

\(dz\)	$$= \frac{\partial z}{\partial x} \:dx + \frac{\partial z}{\partial y} \:dy $$	Total differential \(dz\)
	\(= (2 \sin y - 6xy^{2})\:dx + (2x \cos y - 6x^{2}y) \: dy. \)

b. The total differential \(dw\) for \(w= x^{2} + y^{2} + z^{2} \) is

\(dw\)	$$= \frac{\partial w}{\partial x} \:dx + \frac{\partial w}{\partial y} \:dy + \frac{\partial w}{\partial z} \:dz $$	Total differential \(dw\)
	\(= 2x\:dx + 2y \: dy + 2z \:dz. \)

Differentiability

Definition 13.4.2 Differentiability

A function \(f\) given by \(z=f(x,y)\) is differentiable at \((x_{0}, y_{0})\) if \( \Delta z\) can written in the form

\( \Delta z = f_{x}(x_{0}, y_{0}) \Delta x + f_{y}(x_{0}, y_{0}) \Delta y + \varepsilon_{1} \Delta x + \varepsilon_{2} \Delta y\)

where both \( \varepsilon_{1} \) and \( \varepsilon_{1} \rightarrow 0\) as

\( ( \Delta x, \Delta y ) \rightarrow (0,0)\).

The function \(f\) is differentiable in a region \(R\) if it is differentiable at each point in \(R\).

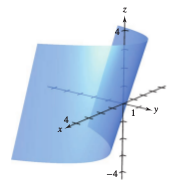
Example 13.4.2 Showing that a Function Is Differentiable

Figure 13.4.1

Show that the function \( f(x,y) = x^{2} + 3y \) is differentiable at every point in the plane. Solution Letting \( z= f(x,y)\), the increment for \(z\) at an arbitrary point \((x,y)\) in the plane is \( \Delta z \) \(= f(x + \Delta x, y+ \Delta y) - f(x,y) \) \(= (x^{2} +2x \Delta x + \Delta x^{2}) + 3(y + \Delta y) - (x^{2} + 3y )\) \(= 2x \Delta x + \Delta x^{2} + 3 \Delta y \) \( = 2x( \Delta x) + 3( \Delta y) + \Delta x ( \Delta x) + 0(\Delta y) \) \(= f_{x}(x,y) 2x \Delta x + f_{y}(x,y) \Delta x^{2} + \varepsilon_{1} \Delta x + \varepsilon_{2} \Delta y \) where \(\varepsilon_{1} = \Delta x \) and \( \varepsilon_{2} = 0 \). Because \(\varepsilon_{1} \rightarrow 0 \) and \( \varepsilon_{2} \rightarrow 0 \) as \((\Delta x, \Delta y) \rightarrow (0,0)\), it follows that \(f\) is differentiable at every point in the plane. The graph for \(f\) is shown in Figure 13.4.1.

Theorem 13.4.1 Sufficient Conditions for Differentiability

The term differentiable is used differently for functions with two variables than for functions with one variable. A function with one variable is differentiable at a point when its derivative exists at the point. For a function with two variables, that the partial derivatives \(f_{x}\) and \(f_{y}\) exist does not guarantee that the function is differentiable.

If \(f\) is a function for \(x\) and \(y\), where \(f_{x}\) and \(f_{y}\) are continuous in an open region \(R\), then \(f\) is differentiable on \(R\).

A function with three variables \(w=f(x,y,z)\) is differentiable at \((x,y,z)\) provided that

\( \Delta w=f(x + \Delta x,y + \Delta y,z+ \Delta z) - f(x,y,z)\)

can be written in the form

\( \Delta w=f_{x} \Delta x + f_{y} \Delta y + f_{z} \Delta z + \varepsilon_{1} \Delta x + \varepsilon_{2} \Delta y + \varepsilon_{3} \Delta z \)

where \(\varepsilon_{1}\), \(\varepsilon_{2}\), and \(\varepsilon_{3} \rightarrow 0\) as \(( \Delta x, \Delta y, \Delta z) \rightarrow(0,0,0)\).

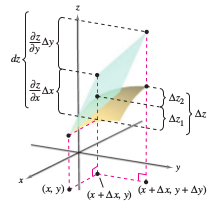
Approximation by Differentials

The exact change in \(z\) is \( \Delta z\) and is approximated by the differential \(dz\). Figure 13.4.2

Theorem 13.4.1 states that choosing \((x+ \Delta x, y + \Delta y)\) close enough to \((x,y)\) can make \( \varepsilon_{1} \Delta x\) and \(\varepsilon_{2} \Delta y\) insignificant. For small \(\Delta x \) and \( \Delta y\), the approximation \( \Delta z \approx dz \). This means that $$ dz = \frac{\partial z}{\partial x} \Delta x + \frac{\partial z}{\partial y} \Delta y $$ represents the change in altitude for a plane that is tangent to the surface at the point \((x,y,f(x,y))\). Because a plane in three-dimensions is represented by a linear equation in the variables \(x\), \(y\), and \(z\), the approximation for \(\Delta z \) by \(dz\) is called a linear approximation.

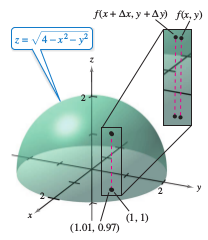
Example 13.4.3 Using a Differential as an Approximation

As \((x,y)\) moves from \((1,1)\) to the point \((1.01,0.97)\), the value for \((x,y)\) changes by 0.0137. Figure 13.4.3

Use the differential \(dz\) to approximate the change in \(z=\sqrt{4-x^{2}-y^{2}} \) as \((x,y)\) moves from \((1,1)\) to the point \((1.01, 0.97)\). Compare this approximation with the exact change in \(z\). Solution Letting \((x,y) = (1,1)\) and \((x + \Delta x, y + \Delta y) = (1.01,0.97)\) produces \(dx = \Delta x = 0.01\) and \(dy = \Delta y = -0.03\). The change in \(z\) can be approximated by $$ \Delta z \approx dz = \frac{\partial z}{ \partial x}\: dx + \frac{\partial z}{ \partial y}\: dy = \frac{-x}{\sqrt{4-x^{2}-y^{2}}}\Delta x + \frac{-y}{\sqrt{4-x^{2}-y^{2}}}\Delta y. $$ When \(x=1\) and \(y=1\) the approximation is $$ \Delta z \approx -\frac{1}{\sqrt{2}}(0.01) - \frac{1}{\sqrt{2}}(-0.03)= \frac{0.02}{\sqrt{2}} = \sqrt{2}(0.01) \approx 0.0141$$ The exact change corresponds to the difference in height between two points on the hemisphere's surface, as shown in Figure 13.4.3. This difference is given by \( \Delta z\) \(= f(1.01,0.97) - f(1,1) \) \(= \sqrt{4-( \color{red}{1.01} )^{2} - ( \color{red}{0.97})^{2}} - \sqrt{\color{red}{1}^{2}-\color{red}{1}^{2} }\) \( \approx 0.0137. \)

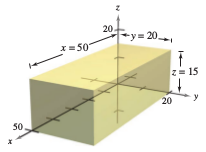
Example 13.4.4 Error Analysis

Volume \(= xyz\) Figure 13.4.4

The possible error in measuring a rectangular box along each dimension is \(\pm 0.1\) millimeter. The dimensions are \(x=50\) centimeters, \(y=20\) centimeters, and \(z=15\) centimeters, as shown in Figure 13.4.4. Use \(dV\) to estimate the propagated error and the relative error in calculating the volume. Solution The boxes volume is \(V=xyz\), therefore \(dV\) $$= = \frac{\partial V}{ \partial x}\: dx + \frac{\partial V}{ \partial y}\: dy + \frac{\partial V}{ \partial z}\: dz $$ \(= yz\:dx + xz\:dy + xy\:dz. \) Using 0.1 millimeter = 0.01 centimeter yields \(dx=dy=dz= \pm 0.01\) and the propagated error is approximately \(dV\) \(=(20)(15)(\pm 0.01) + (50)(15)(\pm0.01) + (50)(20)(\pm0.01) \) \(= 300(\pm0.01) + 750(\pm 0.01)+ 1000(\pm 0.01)\) \(= 2050(\pm 0.01)\) \(= \pm 20.5 \) cubic centimeters. Because the measured volume is \(V = (50)(20)(15) = 15,000 \) cubic centimeters, the relative error, \(\Delta V/V\), is approximately $$ \frac{ \Delta V}{V} \approx \frac{dV}{V} = \frac{20.5}{15,000} \approx 0.14 \text{%.}$$

Theorem 13.4.2 Differentiability Implies Continuity

If a function for \(x\) and \(y\) is differentiable at \((x_{0},y_{0})\), then it is continuous at \(x_{0},y_{0})\).
Proof Let \(f\) be differentiable at \((x_{0},y_{0})\), where \(z=f(x,y)\). Then

\(\Delta z = [f_{x}(x_{0},y_{0}) + \varepsilon_{1}] \Delta x + [f_{y}(x_{0},y_{0}) + \varepsilon_{2}] \Delta y \)

where both \( \varepsilon_{1}\) and \( \varepsilon_{1} \rightarrow 0 \) as \((\Delta x, \Delta y) \rightarrow (0,0)\). By definition,

\( \Delta z = f( x_{0} + \Delta x,y_{0} + \Delta y) - f(x_{0},y_{0})\).

Letting \(x = x_{0} + \Delta x\) and \(y = y_{0} + \Delta y\) produces

\(f(x,y) - f(x_{0},y_{0}) \)	\(= [f_{x}(x_{0},y_{0}) + \varepsilon_{1}] \Delta x + [f_{y}(x_{0},y_{0}) + \varepsilon_{2}] \Delta y \)
	\(= [f_{x}(x_{0},y_{0}) + \varepsilon_{1}] (x - x_{0}) + [f_{y}(x_{0},y_{0}) + \varepsilon_{2}] (y - y_{0}). \)

Taking the limit as \((x,y) \rightarrow (x_{0},y_{0})\) produces

$$ \lim_{(x,y) \rightarrow (x_{0},y_{0})} f(x,y) = f(x_{0},y_{0})$$

which means that \(f\) is continuous at \((x_{0},y_{0})\).

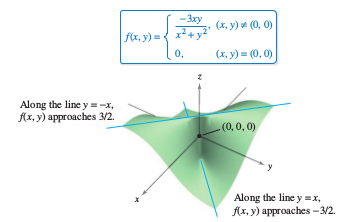
Example 13.4.5 A Function That Is Not Differentiable

Just because \(f_{x}\) and \(f_{y}\) exist does not mean the function is differentiable.
For the function

$$ f(x,y) = \left\{\begin{matrix} \frac{-3xy}{x^{2}+y^{2}}, & (x,y) \ne (0,0) \\ 0, & (x,y)=(0,0) \end{matrix}\right. $$

shows that \(f_{x}(0,0)\) and \(f_{y}(0,0)\) both exist, but that \(f\) is not differentiable at \((0,0)\).
Solution Show that \(f\) is not differentiable at \((0,0)\) by showing that it is not continuous there. Determine the limits along two directions as each approaches \((0,0)\), as shown in Figure 13.4.5. Along the line \(y=x\), the limit is

Figure 13.4.5

Internal Links

Parent Article: Calculus III 13 Functions with Several Variables