Calculus III 13.05 Chain Rules for Functions with Several Variables

Previous	Calculus III 13.04 Differentials
Next	Calculus III 13.06 Directional Derivatives and Gradients

13.05 Chain Rules for Functions with Several Variables

• Use the Chain Rules for functions with several variables.
• Find partial derivatives implicitly.

Chain Rules for Functions with Several Variables

Chain Rule Illustrated Figure 13.5.1

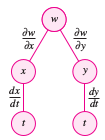
The Chain Rule can be extended to functions with two or more variables in two cases. The first case is \(w\) as a function for \(x\) and \(y\), where \(x\) and \(y\) are functions with a single independent variable \(t\), as shown in Theorem 13.5.1. Theorem 13.5.1 Chain Rule: One Independent Variable Let \(w=f(x,y)\), where \(f\) is a differentiable function for \(x\) and \(y\). If \(x=g(t)\) and \(y=h(t)\), where \(g\) and \(h\) are differentiable functions for \(t\), then \(w\) is a differentiable function for \(t\), and $$\frac{dw}{dt} = \frac{\partial w}{\partial x}\frac{dx}{dt} + \frac{\partial w}{\partial y}\frac{dy}{dt}.$$ The Chain Rule is shown in Figure 13.5.1 This can be extended to multiple variables. For example, if each \(x_{i}\) is a differentiable function for a single variable \(t\), then for \( w = f(x_{1},x_{2},...,x_{n}) \) produces $$\frac{dw}{dt} = \frac{\partial w}{\partial x_{1}}\frac{dx_{1}}{dt} + \frac{\partial w}{\partial x_{2}}\frac{dx_{2}}{dt} + \cdot \cdot \cdot + \frac{\partial w}{\partial x_{n}}\frac{dx_{n}}{dt}. $$

Example 13.5.1 Chain Rule with One Independent Variable

Let \(w = x^{2}y - y^{2}\), where \(x = \sin t\) and \(y=e^{t}\). Find \(dw/dt\) where \(t=0\).
Solution Applying Theorem 13.5.1 produces

$$\frac{dw}{dt}$$	$$ = \frac{\partial w}{\partial x}\frac{dx}{dt} + \frac{\partial w}{\partial y}\frac{dy}{dt}$$
	\(= 2 xy(\cos t) + (x^{2}-2y)e^{t} \)
	\(= 2 (\sin t)(e^{t})( \cos t) + ( \sin^{2} t - 2e^{t})e^{t} \)
	\( = 2e^{t} \sin t \cos t + e^{t} \sin^{2} t -2 e^{t}\).

$$ \frac{dw}{dt}=-2 \: \text{ when } t=0 $$

Using single variable techniques to find \(dw/dt\) by first writing \(w\) as a function for \(t\),

\(w\)	\(= x^{2}y - y^{2} \)
	\(= (\sin t)^{2}(e^{t})-(e^{t})^{2}\)
	\(=(e^{t}) \sin^{2} t - e^{2t} \)

and then differentiating as usual.

$$ \frac{dw}{dt} = 2e^{2t} \sin t \cos t + e^{t} \sin^{2} t - 2e^{2t} $$

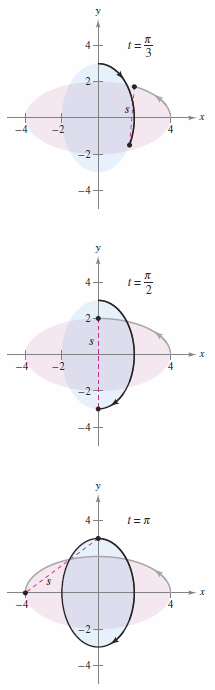
Example 13.5.2 Applying the Chain Rule to Related Rates

Paths for two objects traveling in elliptical orbits. Figure 13.5.2

Two objects are traveling in elliptical paths given by the following parametric equations. \(x_{1}\) \(= 4 \cos t \) and \(y_{1}\) \(= 2 \sin t\) First Object \(x_{2}\) \(= 2 \sin 2t \) and \(y_{2}\) \(= 3 \cos 2t \:\:\:\: \) Second Object At what rate is the distance between the two objects changing when \(t= \pi\)? Solution The distance \(s\) between the objects is given by \( s = \sqrt{ (x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2}} \) as shown in Figure 13.5.2. When \(t=0\) \(x_{1}\) \(=-4 \) \(y_{1}\) \(= 0 \) \(x_{2}\) \(=0 \) \(y_{2}\) \(= 3 \) and \( s = \sqrt{ (0+4)^{2} + (3-0)^{2}}= 5. \) When \(t=\pi\), the partial derivatives for \(s\) are $$\frac{ \partial s}{ \partial x_{1}} $$ $$= \frac{ -(x_{2}-x_{1})}{\sqrt{ (x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2}} }= - \frac{1}{5}(0+4) = - \frac{4}{5}$$ $$\frac{ \partial s}{ \partial y_{1}} $$ $$= \frac{ -(y_{2}-y_{1})}{\sqrt{ (x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2}} }= - \frac{1}{5}(3-0) = - \frac{3}{5}$$ $$\frac{ \partial s}{ \partial x_{2}} $$ $$= \frac{ (x_{2}-x_{1})}{\sqrt{ (x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2}} }= \frac{1}{5}(0+4) = \frac{4}{5}$$ $$\frac{ \partial s}{ \partial y_{2}} $$ $$= \frac{ (y_{2}-y_{1})}{\sqrt{ (x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2}} }= \frac{1}{5}(3-0) = \frac{3}{5}$$ When \(t=\pi\), the derivatives for \(x_{1}\), \(y_{1}\), \(x_{2}\), and \(y_{2}\) are $$ \frac{d x_{1}}{dt} $$ \(= -4 \sin t = 0\) $$ \frac{d y_{1}}{dt} $$ \(= 2 \cos t = -2 \) $$ \frac{d x_{2}}{dt} $$ \(= 4 \cos 2t = 4 \) $$ \frac{d y_{2}}{dt} $$ \(= -6 \sin 2t = 0 \) Applying the Chain Rule produces the change rate $$ \frac{d s}{d t} $$ $$= \frac{ \partial s}{ \partial x_{1}} \frac{d x_{1}}{d t} + \frac{ \partial s}{ \partial y_{1}}\frac{d y_{1}}{d t} + \frac{ \partial s}{ \partial x_{2}} \frac{d x_{2}}{d t} +\frac{ \partial s}{ \partial y_{2}} \frac{d y_{2}}{d t}$$ $$ = \left( - \frac{4}{5} \right)(0) + \left( - \frac{3}{5} \right)(2) + \left( \frac{4}{5} \right)(4) + \left( \frac{3}{5} \right)(0) $$ $$ = \frac{22}{5}$$

In Example 13.5.2, note that \(s\) is the function with four intermediate variables, \(x_{1}\), \(y_{1}\), \(x_{2}\), and \(y_{2}\), each is a function with a single variable \(t\). Another composite function type is one where the intermediate variables are themselves functions with more than one variable. For instance, for \(w=f(x,y)\), where \(x=g(s,t)\) and \(y=h(s,t)\), it follows that \(w\) is a function for \(s\) and \(t\). The partial derivatives for \(w\) are considered with respect to \(s\) and \(t\). One way to find these partial derivatives is to write \(w\) as a function for \(s\) and \(t\) explicitly by substituting the equations \(x=g(s,t)\) and \(y=h(s,t)\) into the equation \(w=f(x,y)\). Then the partial derivatives are found in the usual way, as demonstrated in Example 13.5.3.

Example 13.5.3 Finding Partial Derivatives by Substitution

Find \(\partial w/ \partial s\) and \(\partial w/ \partial t\) for \(w=2xy\), where \(x=s^{2}+t^{2}\) and \(y=s/t\).
Solution Begin by substituting \(x=s^{2}+t^{2}\) and \(y=s/t\) into the equation \(w=2xy\) to obtain

$$ w=2xy = 2(s^{2}+t^{2}) \left( \frac{s}{t}\right) = 2 \left( \frac{s^{2}}{t} + st \right).$$

To find \(\partial w/ \partial s\), hold \(t\) constant and differentiate with respect to \(s\).

$$ \frac{\partial w}{ \partial s} $$	$$= 2 \left( \frac{3s^{2}}{t} + t \right) $$
	$$= \frac{6s^{2}+2t^{2}}{t}$$

To find \(\partial w/ \partial t\), hold \(s\) constant and differentiate with respect to \(t\) to obtain

$$ \frac{\partial w}{ \partial t} $$	$$= 2 \left( - \frac{s^{2}}{t^{2}} + s \right) $$
	$$= 2 \left( \frac{-s^{2} + st^{2}}{t^{2}} \right) $$
	$$= \frac{-2st^{2} + 2s^{3}}{t^{2}}.$$

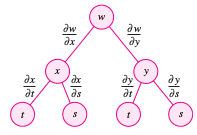
Theorem 13.5.2 Chain Rule: Two Independent Variables

Chain Rule: two independent variables Figure 13.5.3

Let \(w=f(x,y)\), where \(f\) is a differentiable function for \(x\) and \(y\). If \(x=f(s,t)\) and \(y=h(s,t)\) such that the first partials \(\partial x/ \partial s\), \(\partial x/ \partial t\), \(\partial y/ \partial s\), and \(\partial y/ \partial t\) all exist, the \(\partial w/ \partial s\) and \(\partial w/ \partial t\) exist and are given by $$ \frac{\partial w}{ \partial s} = \frac{\partial w}{ \partial x} \frac{\partial x}{ \partial s} + \frac{\partial w}{ \partial y}\frac{\partial y}{ \partial s} $$ and $$ \frac{\partial w}{ \partial t} = \frac{\partial w}{ \partial x} \frac{\partial x}{ \partial t} + \frac{\partial w}{ \partial y}\frac{\partial y}{ \partial t} $$ as shown in Figure 13.5.3. Proof To obtain \( \partial w / \partial s\), hold \(t\) constant and apply Theorem 13.5.1 to obtain the desired result. Similarly, for \( \partial w / \partial s\), hold \(s\) constant and apply Theorem 13.5.1. This extends to functions with multiple variables. For example, if \(w\) is a differentiable function with \(n\) variables. \(x_{1},x_{2},...,x_{n}\) where each \(x_{1}\) is a differentiable function for the \(m\) variables \(t_{1},t_{2},...,t_{n}\), then for \(w=f(x_{1},x_{2},...,x_{n})\) produces the following $$ \frac{\partial w}{ \partial t_{1}} $$ $$= \frac{\partial w}{ \partial x_{1}} \frac{\partial x_{1}}{ \partial t_{1}} + \frac{\partial w}{ \partial x_{2}}\frac{\partial x_{2}}{ \partial t_{1}} + \cdot \cdot \cdot + \frac{\partial w}{ \partial x_{x}}\frac{\partial x_{n}}{ \partial t_{1}} $$ $$ \frac{\partial w}{ \partial t_{2}} $$ $$= \frac{\partial w}{ \partial x_{1}} \frac{\partial x_{1}}{ \partial t_{2}} + \frac{\partial w}{ \partial x_{2}}\frac{\partial x_{2}}{ \partial t_{2}} + \cdot \cdot \cdot + \frac{\partial w}{ \partial x_{x}}\frac{\partial x_{n}}{ \partial t_{2}} $$ $$\vdots $$ $$ \frac{\partial w}{ \partial t_{m}} $$ $$= \frac{\partial w}{ \partial x_{1}} \frac{\partial x_{1}}{ \partial t_{m}} + \frac{\partial w}{ \partial x_{2}}\frac{\partial x_{2}}{ \partial t_{m}} + \cdot \cdot \cdot + \frac{\partial w}{ \partial x_{x}}\frac{\partial x_{n}}{ \partial t_{m}} $$

Example 13.5.4 The Chain Rule with Two Independent Variables

Use the Chain Rule to find \(\partial w/ \partial s\) and \(\partial x/ \partial t\) for

\( w=2xy \)

where \(x = s^{2}+t^{2}\) and \( y = s/t\).
Solution Note that these same partials were found in Example 13.5.3. Using Theorem 13.5.2, hold \(t\) constant and differentiate with respect to \(s\) to obtain

$$ \frac{\partial w}{ \partial s} $$	$$ = \frac{\partial w}{ \partial x} \frac{\partial x}{ \partial s} + \frac{\partial w}{ \partial y}\frac{\partial y}{ \partial s} $$
	$$= 2y(2s)+ 2x \left( \frac{1}{t} \right) $$
	$$ = 2 \left(\color{red}{ \frac{2}{t}} \right)(2s) + 2 (\color{red}{ s^{2}+t^{2} }) \left( \frac{1}{t} \right) \:\:\:\: $$	Substitute \(\frac{2}{t}\) for \(y\) and \(s^{2}+t^{2}\) for \(x\).
	$$= \frac{4s^{2}}{t} + \frac{2s^{2}+2t^{2}}{t} $$
	$$ = \frac{6s^{2}+2t^{2}}{t}. $$

Holding \(s\) constant gives

$$ \frac{\partial w}{ \partial t} $$	$$ = \frac{\partial w}{ \partial x} \frac{\partial x}{ \partial t} + \frac{\partial w}{ \partial y}\frac{\partial y}{ \partial t} $$
	$$= 2y(2t)+ 2x \left( \frac{-s}{t^{2}} \right) $$
	$$ = 2 \left(\color{red}{ \frac{2}{t}} \right)(2t) + 2 (\color{red}{ s^{2}+t^{2} }) \left( \frac{-s}{t^{2}} \right) \:\:\:\: $$	Substitute \(\frac{2}{t}\) for \(y\) and \(s^{2}+t^{2}\) for \(x\).
	$$= 4s - \frac{2s^{3}+2st^{2}}{t^{2}}$$
	$$ = \frac{4st^{2} - 2s^{3} -2st^{2}}{t^{2}}. $$
	$$ = \frac{2st^{2} - 2s^{3}}{t^{2}}. $$

Example 13.5.5 The Chain Rule with Three Independent Variables

Find \(\partial w/ \partial s\) and \(\partial w/ \partial t\) when\(s=1\) and \(t=2 \pi\) for

\( w =xy + yz + xz \)

where \(x=s \cos t\), \(y=s \sin t\), and \(z=t\).
Solution Applying Theorem 13.5.2 produces

$$ \frac{\partial w}{ \partial s} $$	$$= \frac{\partial w}{ \partial x} \frac{\partial x}{ \partial s} + \frac{\partial w}{ \partial y}\frac{\partial y}{ \partial s} + \frac{\partial w}{ \partial z}\frac{\partial z}{ \partial s}$$
	\(= (y+z)(\cos t) + (x+z)(\sin t) + (y+x)(0)\)
	\(= (y+z)(\cos t) + (x+z)(\sin t) \)

When \(s=1\) and \(t=2\pi\), \(x=1\), \(y=0\), and \(z=2\). Therefore,

$$ \frac{\partial w}{ \partial s} = (0+ 2\pi)(1)+(1 + 2 \pi)(0) = 2 \pi$$

Furthermore,

$$ \frac{\partial w}{ \partial t} $$	$$= \frac{\partial w}{ \partial x} \frac{\partial x}{ \partial t} + \frac{\partial w}{ \partial y}\frac{\partial y}{ \partial t} + \frac{\partial w}{ \partial z}\frac{\partial z}{ \partial t}$$
	\(= (y+z)(-s \sin t) + (x+z)(s \cos t) + (y+x)(1)\)

and for \(s=1\) and \(t=2 \pi\), it follows that

$$ \frac{\partial w}{ \partial t} $$	\(= (0+2 \pi)(0) + (1+2 \pi)(1) + (0+1)(1)\)
	\(= 2 + 2 \pi\)

Implicit Partial Differentiation

Let \(x\) and \(y\) be related by the equation \(F(x,y)=0\), where \(y=f(x)\) is a differentiable function for \(x\). The Chain Rule can be applied to find the derivatives. Consider the function

\(w=F(x,y) = F(x,f(x))\).

Applying Theorem 13.5.2 yields

$$ \frac{dw}{dx} = F_{x}(x,y)\frac{dx}{dx}+ F_{y}(x,y)\frac{dy}{dx}. $$

Because \(w=F(x,y) = 0 \) for all \(x\) in \(f\)'s domain it follows that

$$ \frac{dw}{dx} = 0 $$

and produces

$$ F_{x}(x,y)\frac{dx}{dx}+ F_{y}(x,y)\frac{dy}{dx} = 0. $$

If \(F_{x}(x,y) \ne 0 \), use the fact that \(dx/dx = 1\) to conclude that

$$ \frac{dy}{dx} = - \frac{F_{x}(x,y)}{F_{y}(x,y)}. $$

A similar procedure can find the partial derivatives for functions with several variables that are defined implicitly.

Theorem 13.5.3 Chain Rule: Implicit Differentiation

If the equation \(F(x,y)=0\) defines \(y\) implicitly as a differentiable function for \(x\), then

$$ \frac{dy}{dx} = - \frac{F_{x}(x,y)}{F_{y}(x,y)}, \: F_{y}(x,y) \ne 0.$$

If the equation \(F(x,y,z)=0\) defines \(z\) implicitly as a differentiable function for \(x\) and \(y\), then

$$ \frac{dz}{dx} = - \frac{F_{x}(x,y,z)}{F_{z}(x,y,z)} \text{ and } \frac{dz}{dy} = - \frac{F_{y}(x,y,z)}{F_{z}(x,y,z)}, \: F_{z}(x,y,z) \ne 0.$$

This theorem can be extended to functions defined implicitly with any variable count.

Example 13.5.6 Finding a Derivative Implicitly with Two Variables

Find \(dy/dx\) for

\(y^{3}+y^{2}-5y-x^{2}+4=0.\)

Solution Begin by letting

\(F(x,y) = y^{3}+y^{2}-5y-x^{2}+4.\)

Then

\( F_{x}(x,y)= -2x \) and \( F_{y}(x,y)= 3y^{2}+2y-5. \)

Applying Theorem 13.5.3 produces

$$ \frac{dy}{dx} = - \frac{F_{x}(x,y)}{F_{y}(x,y)} = \frac{ - (\color{red}{-2x})}{\color{red}{3y^{2}+2y-5}} = \frac{-2x}{3y^{2}+2y-5}. $$

Example 13.5.7 Finding a Derivative Implicitly with Three Variables

Find \(dz/dx\) and \(dz/dy\) for

\( 3x^{2}z - x^{2}y^{2} + 2z^{3} + 3yz -5 = 0. \)

Solution Begin by letting

\( F(x,y,z) = 3x^{2}z - x^{2}y^{2} + 2z^{3} + 3yz -5. \)

Then

\( F_{x}(x,y,z)= 6xz-2xy^{2} \)

\( F_{y}(x,y,z)= -2x^{2}y+3z \)

\( F_{z}(x,y,z)= 3x^{2} + 6z^{2}+3y \)

Applying Theorem 13.5.3 produces

$$ \frac{dz}{dx} = - \frac{F_{x}(x,y,z)}{F_{z}(x,y,z)} = \frac{2xy^{2}-6xz}{3x^{2}+6z^{2}+3y} $$

and

$$ \frac{dz}{dy} = - \frac{F_{y}(x,y,z)}{F_{z}(x,y,z)} = \frac{2x^{2}y-3z}{3x^{2}+6z^{2}+3y}.$$

Internal Links

Parent Article: Calculus III 13 Functions with Several Variables