Calculus III 13.06 Directional Derivatives and Gradients

Previous	Calculus III 13.05 Chain_Rules for Functions with Several Variables
Next	Calculus III 13.07 Tangent Planes and Normal Lines

13.6 Directional Derivatives and Gradients

• Find and use directional derivatives for a function with two variables.
• Find the gradient for a function with two variables.
• Use the gradient for a function with two variables in applications.
• Find directional derivatives and gradients for functions with three variables.

Directional Derivative

Figure 13.6.1 Figure 13.6.2 Figure 13.6.3

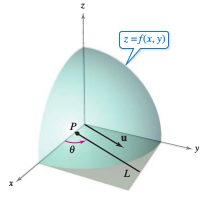
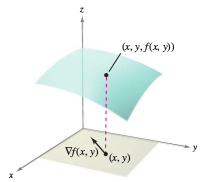
Consider the hillside represented by \(z=f(x,y)\) as shown in Figure 13.6.1 and how to determine its incline toward the \(z\)-axis. Slopes can be determined in two different directions - the slope in the \(y\)-direction is given by the partial derivative \(f_{y}(x,y)\), and the slope in the \(x\)-direction is given by the partial derivative \(f_{x}(x,y)\). These two partial derivatives can be used to find the slope in any direction. To determine the slope at a point on a surface, a new derivative is needed, called a directional derivative. Begin by letting \(z=f(x,y)\) be a surface and \(P(x_{0},y_{0})\) be a point in the domain for \(f\), as shown in Figure 13.6.2. 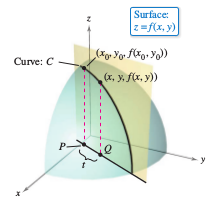The direction for the directional derivative is given by a unit vector \( \textbf{u} = \cos \theta \textbf{i} + \sin \theta \textbf{j} \) where \( \theta \) is the angle the vector makes with the positive \(x\)-axis. To find the desired slope, reduce the problem to two dimensions by intersecting the surface with a vertical plane passing through the point \(P\) and parallel to \(\textbf{u}\), as shown in Figure 13.6.3. This vertical plane intersects the surface to form a curve \(C\). The surface's slope at \((x_{0},y_{0},f(x_{0},y_{0}))\) in \(\textbf{u}\)'s direction is defined as the slope for the curve \(C\) at that point. Informally, the slope for the curve \(C\) has a limit that looks much like those used in single-variable calculus. The vertical plane used to form \(C\) intersects the \(xy\)-plane in a line \(L\), represented by the parametric equations. \(x=x_{0} + t \cos \theta \) and \(y=y_{0} + t \sin \theta \) so that for any value for \(t\), the point \(Q(x,y)\) lies on the line \(L\). For each point \(P\) and \(Q\), there is a corresponding point on the surface. \( (x_{0},y_{0},f(x_{0},y_{0})) \:\:\:\: \) Point above \(P\) \( (x,y,f(x,y)) \) Point above \(Q\) Because the distance between \(P\) and \(Q\) is \( \sqrt{ (x-x_{0})^{2} + (y-y_{0})^{2} } \) \(= \sqrt{ (t \cos \theta)^{2} + (t \sin \theta )^{2} } \) \(=|t| \) the slope for the secant line through \( (x_{0},y_{0},f(x_{0},y_{0}))\) and \( (x,y,f(x,y)) \) can be written as $$ \frac{f(x,y) - f(x_{0},y_{0}) }{t} = \frac{ f(x_{0}+ t \cos \theta, y_{0} + t \sin \theta) - f(x_{0},y_{0})}{t} $$ Letting \(t\) approach 0 produces Definition 13.6.1.

Definition 13.6.1 Directional Derivative

Let \(f\) be a function with two variables \(x\) and \(y\) and let \(\textbf{u} = \cos \theta \textbf{i} + \sin \theta \textbf{j} \) be a unit vector. Then the directional derivative for \(f\) in \(\textbf{u}\)'s direction, denoted \(D_{ \textbf{u} }f\), is

$$ D_{ \textbf{u} } f(x,y) = \lim_{t\rightarrow 0} \frac{ f(x+ t \cos \theta, y + t \sin \theta) - f(x,y) }{t} $$

provided this limit exists.

Calculating directional derivatives by Definition 13.6.1 is similar to finding the derivative for a function with one variable by the limit process. A simpler “working” formula for finding directional derivatives involves the partial derivatives \(f_{x}\) and \(f_{y}\).

Figure 13.6.4

Theorem 13.6.1 Directional Derivative If \(f\) is a differentiable function for \(x\) and \(y\), then the directional derivative for \(f\) in the direction for the unit vector \( D_{ \textbf{u} } f(x,y) = f_{x}(x,y) \cos \theta + f_{y}(x,y) \sin \theta \). Proof For a fixed point \( (x_{0},y_{0} )\), let \( x=x_{0}+ t \cos \theta \) and \( y=y_{0} + t \sin \theta \). Then, Let \(g(t)=f(x,y)\). Because \(f\) is differentiable, apply the Chain Rule given in Theorem 13.5.1 produces \( g^{\prime}(t) = f_{x}(x,y)x^{\prime}(t) + f_{y}(x,y)y^{\prime}(t) = f_{x}(x,y) \cos \theta + f_{y}(x,y) \sin \theta \). If \(t=0\), then \(x=x_{0}\) and \(y=y_{0}\), so \( g^{\prime}(0) = f_{x}(x_{0},y_{0}) \cos \theta + f_{y}(x_{0},y_{0}) \sin \theta \). By the definition for \( g^{\prime}(t) \), it is also true that \( g^{\prime}(0) \) $$= \lim_{t\rightarrow 0} \frac{g(t)-g(0)}{t} $$ $$= \frac{ f(x_{0}+ t \cos \theta, y_{0} + t \sin \theta) - f(x_{0},y_{0})}{t} $$ Consequently, \(D_{ \textbf{u}} f(x_{0},y_{0}) = f_{x}(x_{0},y_{0}) \cos \theta + f(x_{0},y_{0}) \sin \theta \). 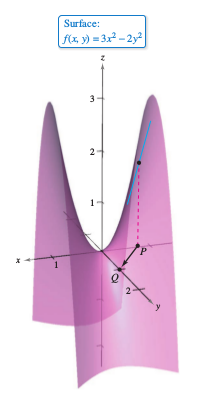There are infinitely many directional derivatives for a surface at a given point—one for each direction specified by \( \textbf{u}\), as shown in Figure 13.6.4. Two are the partial derivatives \(f_{x}\) and \(f_{y}\). 1. Direction for positive \(x\)-axis \(\theta = 0: \: \textbf{u} = \cos 0 \textbf{i} + \sin 0 \textbf{j}= \textbf{i} \) \( D_{\textbf{i}} f(x,y) = f_{x}(x,y) \cos 0 + f_{y}(x,y) \sin 0 = f_{x}(x,y)\) 2. Direction for positive \(y\)-axis $$ \left( \theta = \frac{\pi}{2} \right): \: \textbf{u} = \cos \frac{\pi}{2} \textbf{i} + \sin \frac{\pi}{2} \textbf{j}= \textbf{j} $$ $$ D_{\textbf{j}} f(x,y) = f_{x}(x,y) \cos \frac{\pi}{2} + f_{y}(x,y) \sin \frac{\pi}{2} = f_{y}(x,y) $$

Example 13.6.1 Finding a Directional Derivative

Figure 13.6.5

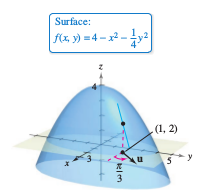
Find the directional derivative for $$f(x,y) = 4-x^{2}- \frac{1}{4} y^{2} \:\:\:\: \color{red}{ \text{ Surface}} $$ at \((1,2)\) in the direction $$ \textbf{u} = \left( \cos \frac{\pi}{3} \right)\textbf{i} + \left( \sin \frac{\pi}{3} \right)\textbf{j} \:\:\:\: \color{red}{ \text{ Direction}}. $$ Solution Because \(f_{x}(x,y)= -2x\) and \(f_{y}(x,y)= -y/2\) are continuous, \(f\) is differentiable, and Theorem 13.6.1 can be applied. $$ D_{ \textbf{u}}f(x,y) = f_{x}(x,y) \cos \theta + f_{y}(x,y) \sin \theta = (-2x) \cos \theta + \left( -\frac{y}{2} \right) \sin \theta $$ Evaluating at \( \theta =\pi /3, \: x=1\), and \(y=2\) produces \(D_{ \textbf{u}}f_{x}(1,2) \) $$= (-2)\left(\frac{1}{2} \right)+ (-1)\left(\frac{\sqrt{3}}{2} \right)$$ $$= -1 - \sqrt{3}{2} $$ \( \approx -1.866 \) as shown in Figure 13.6.5. Figure 13.6.4 can interpret the directional derivative as giving the slope for the surface at the point \((1,2,2)\) in the unit vector \(\textbf{u}\)'s direction.

Example 13.6.2 Finding a Directional Derivative Without a Normal Vector

Figure 13.6.6

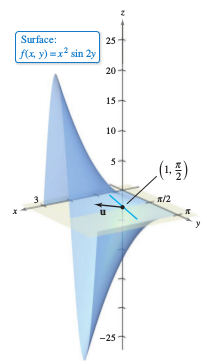
Find the directional derivative for \( f(x,y) = x^{2} \sin 2y \:\:\:\: \)Surface at \((1,\pi/2)\) in the direction \( \textbf{v} = 3 \textbf{i} - 4\textbf{j}. \:\:\:\: \)Direction Solution When the direction is given by a vector whose length is not 1, it must be normalized before applying the formula in Theorem 13.6.1. $$ \textbf{u} = \frac{ \textbf{v} }{ \| \textbf{v} \| } \frac{3}{5} \textbf{i} - \frac{4}{5}\textbf{j} = \cos \theta \textbf{i} + \sin \theta \textbf{j} $$ Using this unit vector produces \( D_{\textbf{u}}f(x,y) \) \(= (2x \sin 2y)(\cos \theta) + (2x^{2} \cos 2y)(\sin \theta) \) $$ D_{\textbf{u}} \left( 1, \frac{\pi}{2} \right) $$ $$=(2 \sin \pi) \left( \frac{3}{5} \right) + (2 \cos \pi)\left( -\frac{4}{5} \right) $$ $$=(0)\left( \frac{3}{5} \right) + (-2) \left( -\frac{4}{5} \right)$$ $$= \frac{8}{5} $$ as shown in Figure 13.6.6.

The Gradient for a Function with Two Variables

The gradient for a function with two variables is a vector-valued function with two variables. This function has many important uses in physics and engineering.

Definition 13.6.2 Gradient for a Function with Two Variables

The gradient for \(f\) is a vector in the \(xy\)-plane. Figure 13.6.7

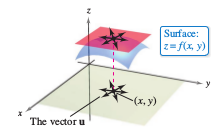
Let \(z=f(x,y)\) be a function for \(x\) and \(y\) such that \(f_{x}\) and \(f_{y}\) exist. Then the gradient for \(f\), denoted by \( \nabla f(x,y)\), is the vector \( \nabla f(x,y) = f_{x}(x,y) \textbf{i} + f_{y}(x,y) \textbf{j}\). Note: The symbol \( \nabla f \) is read as "del \(f\)" or \nabla in LaTeX. Another notation for the gradient is grad \(f(x,y)\). In Figure 13.6.7, note that for each \((x,y)\), the gradient \( \nabla f(x,y) \) is a vector in the plane, two-dimensions, not a vector in space, three-dimensions. Notice that no value is assigned to the symbol \( \nabla \) by itself. It is an operator in the same sense that \( d/dx\) is an operator. When \( \nabla \) operates on \(f(x,y)\), it produces the vector \( \nabla f(x,y)\).

Example 13.6.3 Finding the Gradient for a Function

Find the gradient for

\( f(x,y) = y \ln x + xy^{2} \)

at the point \((1,2)\).
Solution Using

$$ f_{x}(x,y) = \frac{y}{x} + y^{2} \text{ and } f_{y}(x,y) = \ln x +2xy $$

produces

\( \nabla f(x,y) \)	\(= f_{x}(x,y)\textbf{i} + f_{y}(x,y)\textbf{j} \)
	$$= \left( \frac{y}{x} + y^{2} \right)\textbf{i} + (\ln x +2xy) \textbf{j}$$

At the point \((1,2)\), the gradient is

\( \nabla f(1,2) \)	$$= \left( \frac{2}{1} + 2^{2} \right)\textbf{i} + [\ln 1 +2(1)(2)] \textbf{j} $$
	$$= 6\textbf{i} + 4\textbf{j}$$

Theorem 13.6.2 Directional Derivative in Alternative Form

If \(f\) is a differentiable function for \(x\) and \(y\), then the directional derivative for \(f\) in the unit vector \( \textbf{u} \)'s direction is

\( D_{\textbf{u}} f(x,y) = \nabla (x,y) \cdot \textbf{u} \).

Because the gradient for \(f\) is a vector, the directional derivative for \(d\) in \( \textbf{u} \)'s direction can be written as

\( D_{\textbf{u}} f(x,y) = [f_{x}(x,y) \textbf{i} + f_{y}(x,y) \textbf{j}] \cdot [\cos \theta\textbf{i} + \cos \theta\textbf{j}]. \).

The directional derivative is the dot product for the gradient and the direction vector.

Example 13.6.4 Using a Gradient to Find a Directional Derivative

Figure 13.6.8

Find the directional derivative for \( f(x,y) = 3x^{2} -2y^{2} \) at \((-3/4,0)\) in the direction from \(P(-3/4,0)\) to \(Q(0,1)\). Solution Because the partials for \(f\) are continuous, \(f\) is differentiable and Theorem 13.6.2 can be applied. A vector in the specified direction is \( \vec{PQ}\) $$= \left( 0 + \frac{3}{4}\right)\textbf{i} + (1-0)\textbf{j}$$ $$= \frac{3}{4}\textbf{i} + \textbf{j}$$ and a unit vector in this direction is $$ \textbf{u} = \frac{\vec{PQ}}{\| \vec{PQ} \|} = \frac{3}{5}\textbf{i} + \frac{4}{5}\textbf{j}. \:\:\:\: \color{red}{ \text{ Unit vector in }\vec{PQ} \text{'s direction}}$$ Because \(\nabla f(x,y)= f_{x}(x,y) \textbf{i} + f_{y}(x,y) \textbf{j} = 6x\textbf{i} - 4y \textbf{j}\) the gradient at \((-3/4,0)\) is $$ \nabla f\left(- \frac{3}{4},0\right) = - \frac{9}{2}\textbf{i} + 0\textbf{j}. $$ Therefore the direction is $$D_{\textbf{u}} f \left(- \frac{3}{4},0\right) $$ $$= \nabla f \left(- \frac{3}{4},0\right) \cdot \textbf{u} $$ $$= \left( - \frac{9}{2}\textbf{i} + 0\textbf{j} \right) \cdot \left( \frac{3}{5}\textbf{i} + \frac{4}{5}\textbf{j} \right)$$ $$= - \frac{27}{10}$$ as shown in Figure 13.6.8.

Gradient Applications

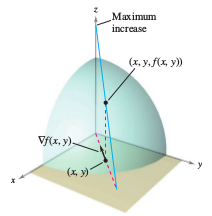
Many applications require in which direction to move so that \(f(x,y)\) increases most rapidly. This direction is called the direction of steepest ascent, and it is given by the gradient, as stated in Theorem 13.6.3.

Theorem 13.6.3 Gradient Properties

The gradient for \(f\) is a vector in the \(xy\)-plane that points in the direction for maximum increase on the surface given by \(z=f(x,y)\). Figure 13.6.9

Let \(f\) be differentiable at the point \((x,y)\). 1. If \( \nabla f(x,y) = \textbf(0)\), then \( D_{\textbf{u}} f(x,y) = 0\) for all \(\textbf{u}\). 2. The direction for the maximum increase in \(f\) is given by \(\nabla f(x,y)\). The maximum value for \( D_{\textbf{u}} f(x,y)\) is \( \| \nabla f(x,y) \|. \:\:\:\: \)Maximum value for \( D_{\textbf{u}} f(x,y)\) 3. The direction for minimum increase for \(f\) is given by \(-\nabla f(x,y)\). The minimum value for \( D_{\textbf{u}} f(x,y)\) is \( -\| \nabla f(x,y) \|. \:\:\:\: \)Minimum value for \( D_{\textbf{u}} f(x,y)\) Proof If \( \nabla f(x,y) = \textbf(0) \), the for any direction, any \( \textbf{u}\), \(D_{\textbf{u}} f(x,y)\) \(= \nabla f(x,y) \cdot \textbf{u} \) \(= (0\textbf{i} + 0\textbf{j}) \cdot (\cos \theta \textbf{i} + \sin \theta \textbf{j} )\) \(= 0.\) If If \( \nabla f(x,y) \ne \textbf(0) \), the let \(\phi \) be the angle between \( \nabla f(x,y) \) and a unit vector \(\textbf{v} \). Using the dot product, Theorem 11.3.2 can be applied, which produces \(D_{\textbf{u}} f(x,y)\) \(= \nabla f(x,y) \cdot \textbf{u} \) \( =\| \nabla f(x,y) \| \|\textbf{u} \| \cos \theta \) \( =\| \nabla f(x,y) \| \cos \theta \) and it follows that the maximum value for \(D_{\textbf{u}} f(x,y)\) will occur when \( \cos \phi = 1.\) Therefore, \( \phi = 0\), and the maximum value for the directional derivative occurs when \( \textbf{u}\) has the same direction as \( \nabla f(x,y) \). This largest value for \(D_{\textbf{u}} f(x,y)\) is precisely \( \| \nabla f(x,y) \| \cos \theta = \| \nabla f(x,y) \| . \) The minimum value for \(D_{\textbf{u}} f(x,y)\) is produced by letting \( \phi = \pi \) so that \( \textbf{u}\) points in the direction opposite from \( \nabla f(x,y) \), as shown in Figure 13.6.9.

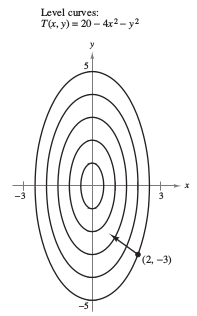
Example 13.6.5 Finding the Direction for Maximum Increase on a Hot Plate

Figure 13.6.10

The temperature in degrees Celsius on a hot plate's surface is \( T(x,y) = 20 -4x^{2} -y^{2} \) where \(x\) and \(y\) are measured in centimeters. In what direction from \((2,-3)\) does the temperature increase most rapidly? What is the increase rate? Solution The function \( \nabla T(x,y)\) gives the direction for the greatest temperature increase at the point \((x,y)\). The gradient is \( \nabla T(x,y)\) \(= T_{x}(x,y) \textbf{i} + T_{y}(x,y) \textbf{j}\) \(= -8x\textbf{i} -2y \textbf{j} \) It follows that the direction for maximum increase is given by \( \nabla T(2,-3) = -16 \textbf{i} +6 \textbf{j}\) as shown in Figure 13.6.10. The increase rate is \( \| \nabla T(2,-3) \| \) \(= \sqrt{256+36} \) \(= \sqrt{296}\) \(\approx 17.09^{\circ}\: \)per centimeter This solution can be misleading. Although the gradient points in the direction for maximum temperature increase, it does not necessarily point toward the hottest spot on the plate. In other words, the gradient provides a local solution to finding an increase relative to the temperature at the point \((2,-3)\). Any other point may have a different direction for maximum increase.

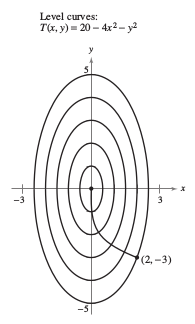
Example 13.6.6 Finding the Path for a Heat-Seeking Particle

Path followed by a heat-seeking particle. Figure 13.6.11

A heat-seeking particle is located at the point \((2,-3)\) on a hot plate whose temperature at \((x,y)\) is \( T(x,y) = 20 -4x^{2} -y^{2} \). Find the particle's path as it continuously moves along the direction for maximum temperature increase. Solution Let the path be represented by the position vector \( \textbf{r}(t) = x(t)\textbf{i} + y(t)\textbf{j} \). A tangent vector at each point \((x(t),y(t))\) is given by $$ \textbf{r}^{\prime}(t) = \frac{dx}{dt}\textbf{i} + \frac{dy}{dt}\textbf{j}. $$ Because the particle seeks maximum temperature increase, the directions for \( \textbf{r}^{\prime}(t) \) and \(\nabla T(x,y)= -8x \textbf{i} -2y\textbf{j} \) are the same at each point on the path. Therefore, $$ -8x = k \frac{dx}{dt} \text{ and } -2y= k\frac{dy}{dt}$$ where \(k\) depends on \(t\). By solving each equation for \(dt/k\) and equating the results yields $$ \frac{dx}{-8x} = \frac{dy}{-2y}. $$ The solution for this differential equation is \(x=Cy^{4}\). Because the particle starts at the point \((2,-3)\), \(C=2/81\). The path for the heat-seeking particle is $$ x= \frac{2}{81}y^{4},$$ as shown in Figure 13.6.11. In Figure 13.6.11 the particle's path, determined by the gradient at each point, is orthogonal to each level curve. This is caused by the temperature \( T(x,y) \) being constant along a given level curve. Therefore, at any point \((x,y)\) on the curve, the change rate for \(T\) in a tangent unit vector \( \textbf{u}\)'s direction is 0. This can be written as \( \nabla f(x,y) \cdot \textbf{u} = D_{\textbf{u}} T(x,y) = 0, \) where \( \textbf{u}\) is a unit tangent vector.

Theorem 13.6.4 Gradient Is Normal to Level Curves

Because

\( \nabla f(x,y) \cdot \textbf{u} = D_{\textbf{u}} T(x,y) = 0, \)

under all conditions, the gradient must be orthogonal, normal, to each level curve.

If \(f\) is differentiable \((x_{0},y_{0})\) and \(\nabla f(x_{0},y_{0}) \ne 0\), then \(\nabla f(x_{0},y_{0})\) is normal to the level curve through \((x_{0},y_{0})\).

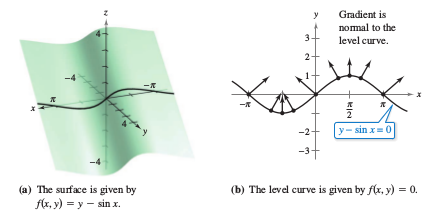
Example 13.6.7 Finding a Normal Vector to a Level Curve

Sketch the level curve corresponding to \(c=0\) for the function given by

\(f(x,y)=y- \sin x\)

and find a normal vector at several point on the curve.
Solution The level curve for \(c=0\) is given by

\( 0 =y- \sin x\)

or

\( y = \sin x\)

as shown in Figure 13.6.12(a). Because the gradient vector for \(f\) at \((x,y)\) is

\( \nabla f(x,y) \)	\(= f_{x}(x,y) \textbf{i} + f_{y}(x,y) \textbf{j} \)
	\(= - \cos x \textbf{i} + \textbf{j}. \)

Applying Theorem 13.6.4 yields that \( \nabla f(x,y) \) is normal to the level curve at the point \((x,y)\). Some gradient vectors are

$$ \nabla f \left( -\pi, 0 \right) $$	$$= \textbf{i} + \textbf{j}$$
$$ \nabla f \left( -\frac{2\pi}{3}, -\frac{ \sqrt{3}}{3} \right) $$	$$= \frac{1}{2}\textbf{i} + \textbf{j}$$
$$ \nabla f \left( -\frac{\pi}{2}, -1 \right) $$	$$= \textbf{j}$$
$$ \nabla f \left( -\frac{\pi}{3}, -\frac{ \sqrt{3}}{3} \right) $$	$$=-\frac{1}{2} \textbf{i} + \textbf{j}$$
$$ \nabla f \left( 0, 0 \right) $$	$$= -\textbf{i} + \textbf{j}$$
$$ \nabla f \left(\frac{\pi}{3},\frac{ \sqrt{3}}{3} \right) $$	$$= -\frac{1}{2} \textbf{i} + \textbf{j}$$
$$ \nabla f \left( \frac{\pi}{2}, 1 \right) $$	$$= \textbf{j}$$
$$ \nabla f \left( -\pi, 0 \right) $$	$$= \textbf{i} + \textbf{j}$$
$$ \nabla f \left( \frac{2\pi}{3}, \frac{ \sqrt{3}}{3} \right) $$	$$= \frac{1}{2}\textbf{i} + \textbf{j}$$
and
$$ \nabla f ( \pi ,0)$$	$$= \textbf{i} + \textbf{j}$$

as shown in Figure 13.6.12(b).

Figure 13.6.12

Functions for Three Variables

The definitions for the directional derivative and the gradient can be extended naturally to functions with three or more variables. As often happens, some geometric interpretation is lost in the generalization from functions with two variables to those with three variables. For example, you cannot interpret the directional derivative for a function with three variables as representing slope.

Definition 13.6.3 Directional Derivative and Gradient for Three Variables

Let \(f\) be a function for \(x\), \(y\), and \(z\), with continuous first partial derivatives. The directional derivative for \(f\) in a unit vector's direction

\( \textbf{u} = a\textbf{i} + b\textbf{j} + c\textbf{k}\)

is given by

\( D_{\textbf{u}} f(x,y,z) = a f_{x}(x,y,z) +b f_{y}(x,y,z) +c f_{z}(x,y,z) . \)

The gradient for \(f\) is defined as

\( \nabla f(x,y,z) = f_{x}(x,y,z)\textbf{i} + f_{y}(x,y,z)\textbf{j} + f_{z}(x,y,z)\textbf{k} . \)

Properties for the gradient are
1. \(D_{\textbf{u}} f(x,y,z) = \nabla f(x,y,z) \cdot \textbf{u} \)
2. If \( \nabla f(x,y,z) = \textbf{0} \), then \(D_{\textbf{u}} f(x,y,z) = 0\) for all \(\textbf{u}\). 3. The direction for maximum increase for \(f\) is given by \(\nabla f(x,y,z)\). The maximum value for \(D_{\textbf{u}} f(x,y,z)\) is

\( \| \nabla f(x,y,z) \|. \:\:\:\:\)Maximum value for \(D_{\textbf{u}} f(x,y,z)\)

4. The direction for minimum increase for \(f\) is given by \(-\nabla f(x,y,z)\). The minimum value for \(D_{\textbf{u}} f(x,y,z)\) is

\( -\| \nabla f(x,y,z) \|. \:\:\:\:\)Minimum value for \(D_{\textbf{u}} f(x,y,z)\)

Theorem 13.6.3 can be generalized to functions with three variables. Under suitable hypotheses,

\( \nabla f(x_{0},y_{0},z_{0}) \)

is normal to the level surface through \( (x_{0},y_{0},z_{0}) \).

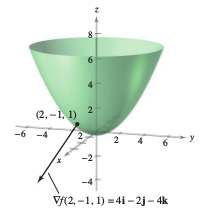
Example 13.6.8 Finding the Gradient for a Function with Three Variables

Figure 13.6.13

Find \( \nabla f(x,y,z) \) for the function \( f(x,y,z) = x^{2}+y^{2}-4z \) and find the direction for maximum increase for \(f\) at the point \((2,-1,1)\). Solution The gradient vector is \( \nabla f(x,y,z) \) \(= f_{x}(x,y,z)\textbf{i} + f_{y}(x,y,z)\textbf{j} + f_{z}(x,y,z)\textbf{k} \) \(= 2x\textbf{i} + 2y\textbf{j} -4\textbf{k} \) It follows the direction for maximum increase at \((2,-1,1)\) is \( \nabla f(2,-1,1) = 4\textbf{i} -2\textbf{j} -4\textbf{k} \) as shown in Figure 13.6.13.

Internal Links

Parent Article: Calculus III 13 Functions with Several Variables