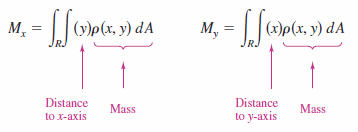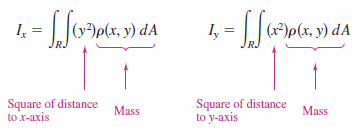Calculus III 14.04 Mass Center and Inertia Moments

Previous	Calculus III 14.03 Double Integrals in Polar Coordinates
Next	Calculus III 14.05 Surface Area

14.04 Mass Center and Inertia Moments[1][2]

• Find the mass for a planar lamina using a double integral.
• Find the mass center for a planar lamina using double integrals.
• Find inertia moments using double integrals.

Mass

Lamina with constant density \(\rho\). Figure 14.4.1

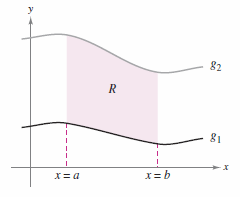
Section 7.6 discussed several applications for integration involving a lamina with constant density \(\rho\). For example, if the lamina corresponding to the region \(R\), as shown in Figure 14.4.1, has a constant density \(\rho\), then the lamina's mass is given by $$Mass =\rho A = \rho \int_{R} \int dA = \int_{R} \int \rho \: dA. \:\:\:\: \color{red}{ \text{Constant density}}$$ If not otherwise stated, a lamina is assumed to have a constant density. This discussion extends lamina to include thin plates with variable density. Double integrals can produce the mass for a lamina with variable density, where the density at \((x,y)\) is given by the density function \rho.

Definition 14.4.1 Mass for a Planar Lamina with Variable Density

If \(\rho\) is a continuous density function on the lamina corresponding to a plane region \(R\), then the mass \(m\) for the lamina is given by

$$m= \int_{R} \int \rho (x,y) \: dA, \:\:\:\: \color{red}{ \text{ Variable density}}$$

Density is normally expressed as mass per unit volume. For a planar lamina, however, density is mass per unit surface area.

Example 14.4.1 Finding the Mass for a Planar Lamina

Lamina with variable density \(\rho(x,y)=2x+y\). Figure 14.4.2

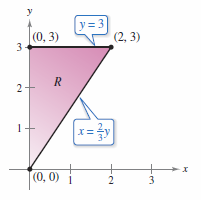
Find the mass for the triangular lamina with vertices \((0,0), \: (0,3) \text{, and }(2,3)\), given that the density at \((x,y)\) is \(\rho(x,y) = 2x+y\), as shown in Figure 14.4.2. The planar lamina is shaded so the darkest shading corresponds to the densest part. Solution The region \(R\) has the boundaries \(x=0\), \(y=3\), or \(x=2y/3\), and \(y=3x/2\). The mass for the lamina is $$m$$ $$= \int_{R} \int (2x+y) \: dA$$ $$= \int_{0}^{3} \int_{0}^{2y/3}(2x+y) \: dx \: dy $$ $$= \int_{0}^{3} \left[ x^{2}+xy \right]_{0}^{2y/3} \: dy $$ \(= \frac{10}{9} \int_{0}^{3} y^{2} \: dy \) \(= \frac{10}{9} \left[ \frac{y^{3}}{3}\right]_{0}^{3} = 10. \)

Example 14.4.2 Finding Mass by Polar Coordinates

Density at \((x,y): \: \rho(x,y)=k\sqrt{x^{2}+y^{2}}\). Figure 14.4.3

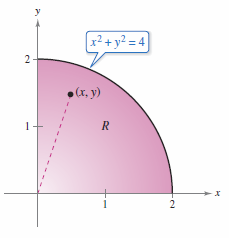
Find the mass for the lamina corresponding to the circle's first-quadrant portion and the origin, as shown in Figure 14.4.3. Solution At any point \((x,y)\), the lamina's density is \( \rho (x,y)\) \(= k \sqrt{(x-0)^{2}+(y-0)^{2}} \) \(= k \sqrt{x^{2}+y^{2}} \) Because the ranges are \(0 \leqslant x \leqslant 2 \) and \(0 \leqslant y \leqslant \sqrt{4-x^{2}} \), the mass produces by $$m $$ $$= \int_{R} \int k \sqrt{x^{2}+y^{2}} \: dA $$ $$= \int_{0}^{2} \int_{0}^{\sqrt{4-x^{2}}} k \sqrt{x^{2}+y^{2}} \:dx \:dy$$ Simplify the integration by converting it to polar coordinates. The new bounds are \(0 \leqslant r \leqslant 2 \) and \(0 \leqslant \theta \leqslant \pi/2 \). The polar mass equation is $$m$$ $$= \int_{0}^{\pi/2} \int_{0}^{2} k \sqrt{r^{2}} r\:dr \: d\theta$$ $$= \int_{0}^{\pi/2} \int_{0}^{2} k r^{2}\:dr \: d\theta$$ $$= \int_{0}^{\pi/2} \left. \frac{1}{3} kr^{3} \right]_{0}^{2} \: d\theta $$ $$= \frac{8k}{3} \int_{0}^{\pi/2} \:d\theta $$ $$= \frac{8k}{3}\left[ \vphantom{\frac{1}{2}} \theta \right]_{0}^{\pi/2} = \frac{4}{3} (\pi k) $$

Moments and Mass Centers

\(M_{x}=(mass)(y_{i}) \\ M_{y}=(mass)(x_{i})\) Figure 14.4.4

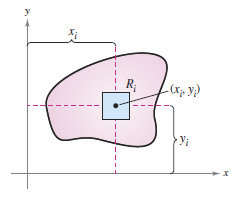
A lamina partition \(\Delta\) corresponding to a plane region \(R\), can be the \(i\)th rectangle \(R_{i}\) for one area \(\Delta A_{i}\), as shown in Figure 14.4.4. Assume the mass for \(R_{i}\) is concentrated at an interior point \((x_{i},y_{i})\). The mass moment for \(R_{i}\) with respect to the \(x\)-axis can be approximated by \((Mass)(y_{i}) \approx [ \rho (x_{i},y_{i}) \Delta A_{i}](y_{i}). \) The mass moment with respect to the \(y\)-axis can be approximated by \((Mass)(x_{i}) \approx [ \rho (x_{i},y_{i}) \Delta A_{i}](x_{i}). \) By forming the Riemann sum for all such products and taking the limits as the norm for \(\Delta\) approaching 0, produces Definition 14.4.1.

Definition 14.4.2 Moments and Mass Center for a Variable Density Planar Lamina

Let \(\rho\) be a continuous density function on the planar lamina \(R\). The mass moments with respect to the \(x\)- and \(y\)-axes are

$$ M_{x}= \int_{R} \int y \rho (x,y)\: dA $$

and

$$ M_{y}= \int_{R} \int x \rho (x,y)\: dA. $$

If \(m\) is the lamina's mass, then the mass center is

$$ (\bar{x},\bar{y}) = \left(\frac{M_{y}}{m}, \frac{M_{x}}{m}\right).$$

If \(R\) represents a simple plane region rather than a lamina, then the point \((\bar{x},\bar{y})\) is called the centroid for the region.

Symmetry can describe the center mass, or a coordinate, for some planar laminas with a constant density \(\rho\). For example, consider the laminas with a constant density shown in Figures 14.4.5 and 14.4.6. In Figure 14.4.5 \(\bar{y}=0\). In Figure 14.4.6 \(\bar{x}=0\).

Lamina with a constant density that is symmetric with respect to the \(x\)-axis. Figure 14.4.5

Lamina with a constant density that is symmetric with respect to the \(y\)-axis. Figure 14.4.6

Example 14.4.3 Finding the Mass Center

Parabolic region with variable density. Figure 14.4.7

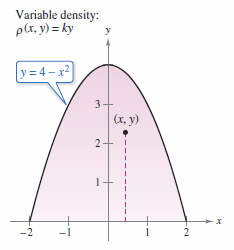
Find the mass center for the lamina corresponding to the parabolic region \( 0 \leqslant y \leqslant 4 - x^{2} \:\:\:\: \color{red}{ \text{Parabolic region}}\) where the density at \((x,y)\) is proportional to the distance between it and the \(x\)-axis, as shown in Figure 14.4.7. Solution The lamina is symmetric with respect to the \(y\)-axis and \(\rho (x,y)=ky\). Therefore, the mass center lies on the \(y\)-axis and \(\bar{x}=0\). Find the lamina's mass to find \(\bar{y}\). $$Mass $$ $$= \int_{-2}^{2} \int_{0}^{4-x^{2}} ky \: dy \: dx$$ $$= \left. \frac{k}{2} \int_{-2}^{2} y^{2} \right]_{0}^{4-x^{2}} \: dx $$ $$= \frac{k}{2} \int_{-2}^{2} (16-8x^{2}+x^{4}) \: dx$$ $$=\frac{k}{2} \left[ 16x- \frac{8x^{3}}{3}+\frac{x^{5}}{5} \right]_{-2}^{2}$$ $$=k \left( 32 - \frac{64}{3} + \frac{32}{5} \right) = \frac{256k}{16}$$ Next, find the moment about the \(x\)-axis. $$M_{x} $$ $$=\int_{-2}^{2} \int_{0}^{4-x^{2}} (y)(ky) \: dy \: dx $$ $$= \left. 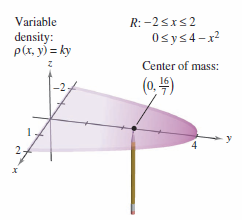\frac{k}{3} \int_{-2}^{2} y^{3} \right]_{0}^{4-x^{2}} \: dx$$ $$= \frac{k}{3} \int_{-2}^{2} (64-48x^{2} + 12x^{4} - x^{6}) \: dx$$ $$= \frac{k}{3} \left[ 64x- 16x^{3}+ \frac{12x^{5}}{5} - \frac{x^{7}}{7} \right]_{-2}^{2} = \frac{4096k}{105}$$ This produces $$ \bar{y}= \frac{M_{x}}{m} = \frac{4096k/105}{256k/15}= \frac{16}{7} $$ with the mass center at \((0,16/7)\).

Figure 14.4.8

Consider the moment mass in Example 14.4.3 as the balancing point for the lamina atop a pencil at \((0,16/7)\), as shown in Figure 14.4.8. While its intuitive to think about the entire mass focused at one point, the mass is really spread out over the entire lamina. The mass moment focused at one point is just a convenience to make many applications using mass easier to solve.

Inertia Moments

The moments \(M_{x}\) and \(M_{y}\) used in determining the mass center for a lamina are sometimes called the first moments about the \(x\)- and \(y\)-axes. The moments are produced by multiplying mass times distance, as shown in Figure 14.4.9.

Figure 14.4.9

The moments about a line are the second moment, or the inertia moment for a lamina about a line. In the same way mass measures matter's tendency to resist change in a straight-line motion, the inertia moment about a line measures matter's tendency to resist change in a rotational motion. For example, when a particle with mass \(m\) is a distance \(d\) from a fixed line, its inertia moment about the line is defined as

\(I=md^{2}=(mass)(distance)^{2}\).

Mass moments can be extended to inertia moments about the \(x\)- and \(y\)-axes for a lamina with variable density. These second moments are denoted by \(I_{x}\) and \(I_{y}\). These are produced by multiplying mass times the distance squared, as shown in Figure 14.4.10.

Figure 14.4.10

When the moments \(I_{x}\) and \(I_{y}\) are summed, the result is called the polar inertia moment and is denoted by \(I_{0}\). For a lamina in the \(xy\)-plane, \(I_{0}\) represents the inertia moment for the lamina about the \(z\)-axis. The term polar inertia moment stems from the fact that the polar distance \(r\) squared is used in the calculation, as shown below.

$$ I_{0} = \int_{R} \int (x^{2}+y^{2}) \rho (x,y) \: dA = \int_{R} \int r^{2} \rho (x,y) \: dA$$

Example 14.4.4 Finding the Inertia Moment

Find the inertia moment about the \(x\)-axis for the lamina described in Example 14.4.3.
Solution The definition for inertia yields,

$$ I_{x}$$	$$= \int_{-2}^{2} \int_{0}^{4-x^{2}} y^{2}(ky) \: dy \: dx$$
	$$= \left. \frac{k}{4} \int_{-2}^{2} y^{4} \right]_{0}^{4-x^{2}} \: dx $$
	$$= \frac{k}{4} \int_{-2}^{2} (256-256x^{2}+96x^{4}- 16x^{6} +x^{8}) \: dx $$
	$$= \frac{k}{4} \left[ 256x-\frac{256x^{3}}{3}+ \frac{96x^{5}}{5}- \frac{16x^{7}}{7} +\frac{x^{9}}{9} \right]_{-2}^{2} = \frac{32,768k}{315}$$

Planar lamina revolving at radians per second. Figure 14.4.11

The inertia moment \(I\) for a revolving lamina can be used to measure its kinetic energy. For example, suppose a planar lamina is revolving about a line with an angular speed at \(\omega\) radians per second, as shown in Figure 14.4.11. The kinetic energy \(E\) for the revolving lamina is $$ E=\frac{1}{2} I \omega^{2}. \:\:\:\: \color{red}{ \text{Kinetic energy for rotational motion}} $$ The kinetic energy for a mass revolving about an axis is proportional to its inertia moment. While moving in a straight line with a velocity \(v\) the kinetic energy \(E\) for a mass \(m\) is $$ E=\frac{1}{2} mv^{2}. \:\:\:\: \color{red}{ \text{Kinetic energy for linear motion}} $$ The kinetic energy for a mass moving in a straight line is proportional to its mass. The gyration radius \(\bar{\bar{r}}\) for a revolving mass \(m\) with inertia moment \(I\) is defined as $$ \bar{\bar{r}}= \sqrt{\frac{I}{m}}. \:\:\:\: \color{red}{ \text{Gyration radius}}$$ If the entire mass were located at a distance \(\bar{\bar{r}}\) from its revolution axis, it would have the same inertia moment and kinetic energy. For example, the gyration radius for the lamina in Example 14.4.4 about the \(x\)-axis is $$\bar{\bar{y}}= \sqrt{\frac{I_{x}}{m}} = \sqrt{\frac{32,768k/315}{256k/15}} = \sqrt{\frac{128}{21}} \approx 2.469.$$

Example 14.4.5 Finding the Gyration Radius

Figure 14.4.12

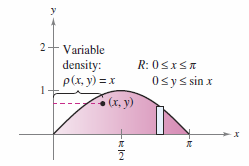
Find the gyration radius about the \(y\)-axis for the lamina corresponding to the region \(R: \: 0 \leqslant y \leqslant \sin x, \: 0 \leqslant x \leqslant \pi, \) where the density at \((x,y)\) is given by \(\rho(x,y) = x\), as shown in Figure 14.4.12. Solution Integrating \(\rho(x,y) = x\) over the region \(R\) yields the mass as \(\pi\). The inertia moment about the \(y\)-axis is $$I_{y} $$ $$= \int_{0}^{\pi} \int_{0}^{\sin x} x^{3} \: dy \: dx $$ $$= \left. \int_{0}^{\pi} x^{3}y \right]_{0}^{\sin x} \: dx $$ $$= \int_{0}^{\pi} x^{3} \sin x \: dx $$ $$=\left[ (3x^{2}-6)(\sin x) - (x^{3}-6x)(\cos x)\right]_{0}^{\pi} = \pi^{3}-6 \pi.$$ The gyration radius about the \(y\)-axis is $$\bar{\bar{x}} $$ $$= \sqrt{ \frac{I_{y}}{m}} $$ $$= \sqrt{\frac{\pi^{3}-6\pi}{\pi}} $$ $$= \sqrt{\pi^{2}-6} \approx 1.967$$

Internal Links

Parent Article: Calculus III 14 Multiple Integration