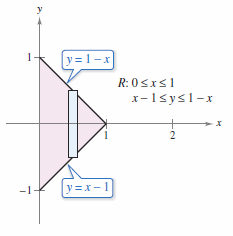Calculus III 14.05 Surface Area

Previous	Calculus III 14.04 Mass Center and Inertia Moments
Next	Calculus III 14.06 Triple Integrals and Applications

14.05 Surface Area

• Using double integrals to find surface area.

Surface Area

Figure 14.5.1 Figure 14.5.2

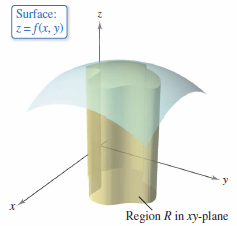
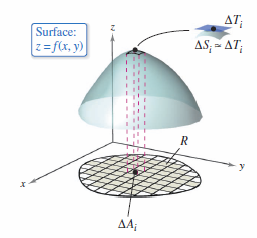
Consider the upper surface area for a solid, as shown in Figure 14.5.1. The surface area \(S\) given by \(z=f(x,y) \:\:\:\: \color{red}{ \text{ Surface defined over region }R}\) defined over a region \(R\). Assume that \(R\) is closed, bounded, and that \(f\) has continuous first partition derivatives. Find the surface area by constructing an inner partition for \(R\) with \(n\) rectangles, where the area for the \(i\)th rectangle \(R_{i}\) is \(\Delta A_{i}=\Delta x_{i} y_{i}\), as shown in Figure 14.5.2. In each \(R_{i}\), let \((x_{i},y_{i})\) be the point that is closest to the origin. At the point \((x_{i},y_{i},z_{i}) = (x_{i},y_{i},f(x_{i},y_{i}))\) on the surface \(S\), construct a tangent plane \(T_{i}\). The \(T_{i}\) portion that lies above \(R_{i}\) is approximately equal to the surface area lying directly above \(R_{i}\). Expressed as an equation, \( \Delta T_{i} \approx \Delta S_{i} \). Therefore, the surface area for \(S\) is approximated by $$ \sum_{i=1}^{n} \Delta S_{i} \approx \sum_{i=1}^{n} \Delta T_{i}.$$ To find the area for the parallelogram \( \Delta T_{i} \), note that its sides are bounded by the vectors \( \textbf{u}= \Delta x_{i} \textbf{i} + f_{x}(x_{i},y_{i}) \Delta x_{i} \textbf{k} \) and \( \textbf{v}= \Delta y_{i} \textbf{i} + f_{y}(x_{i},y_{i}) \Delta y_{i} \textbf{k}. \) From Theorem 11.4.2, the area for \( \Delta T_{i} \) is given by \(\| \textbf{u} \times \textbf{v} \| \), where \( \textbf{u} \times \textbf{v} \) $$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ \Delta x_{i} & 0 & f_{x}(x_{i},y_{i}) \Delta x_{i} \\ 0 & \Delta y_{i} & f_{y}(x_{i},y_{i}) \Delta y_{i} \end{vmatrix}$$ \(= - f_{x}(x_{i},y_{i}) \Delta x_{i} \Delta y_{i} \textbf{i} - f_{y}(x_{i},y_{i}) \Delta x_{i} \Delta y_{i} \textbf{j} + \Delta x_{i} \Delta y_{i} \textbf{k}\) \(= (- f_{x}(x_{i},y_{i})\textbf{i} - f_{y}(x_{i},y_{i})\textbf{j} + \textbf{k} ) \Delta A_{i}.\) The surface area for \( \Delta T_{i} \) is $$\| \textbf{u} \times \textbf{v} \| = \sqrt{[f_{x}(x_{i},y_{i})]^{2} + [f_{y}(x_{i},y_{i})]^{2} +1 } \Delta A_{i},$$ and Surface area for \(S\) $$ \approx \sum_{i=1}^{n} \Delta S_{i}$$ $$ \approx \sum_{i=1}^{n} \sqrt{[f_{x}(x_{i},y_{i})]^{2} + [f_{y}(x_{i},y_{i})]^{2} +1 } \Delta A_{i}. $$ This relationship is described in Definition 14.5.1.

Definition 14.5.1 Surface Area

If \(f\) and its first partial derivatives are continuous on the closed region \(R\) in the \(xy\)-plane, then the surface area \(S\) given by \(z=f(x,y)\) over \(R\) is defined as

Surface area	$$= \int_{R} \int \: dS$$
	$$ = \int_{R} \int \sqrt{ 1 + [f_{x}(x_{i},y_{i})]^{2} + [f_{y}(x_{i},y_{i})]^{2} } \: d A. $$

Example 14.5.1 The Surface Area for a Plane Region

Figure 14.5.3

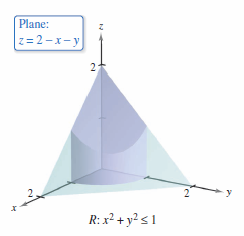
Find the surface area for the plane \(z=2-x-y\) that lies above the circle \(x^{2}+y^{2} \leqslant 1 \) in the first quadrant, as shown in Figure 14.5.3. Solution Because \(f_{x}(x,y) = -1\) and \(f_{y}(x,y) = -1\), the surface area is given by $$ S$$ $$=\int_{R} \int \sqrt{ 1 + [f_{x}(x_{i},y_{i})]^{2} + [f_{y}(x_{i},y_{i})]^{2} } \: d A $$     Formula for surface area $$= \int_{R} \int \sqrt{ 1 + (-1)^{2} + (-1)^{2} } \: d A $$     Substitute $$= \int_{R} \int \sqrt{3} \: d A$$ $$= \sqrt{3} \int_{R} \int \: d A.$$ Note that the last integral is \(\sqrt{3} \) times the area for the region \(R\). Since \(R\) is a quarter circle with radius 1, with an area \( 1/4 \pi (1^{2})\) or \(\pi /4\). The area for \(S\) is $$S $$ $$=\sqrt{3} \text{ (area for }R $$ $$= \sqrt{3} \left( \frac{\pi}{4}\right)= \frac{\sqrt{3} \pi}{4} .$$

Example 14.5.2 Finding Surface Area

Figure 14.5.4 Figure 14.5.5

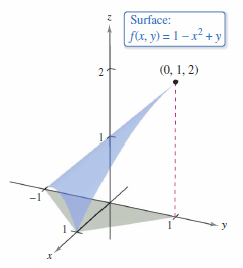
Find the area for the surface \( f(x,y)=1-x^{2}+y\) that lies above the triangular region with vertices \((1,0,0),\: (0,-1,0)\), and \((0,1,0)\), as shown in Figure 14.5.4. Solution Since \(f_{x}(x,y)=-2x\) and \(f_{y}(x,y)=1\), the area is $$S $$ $$= \int_{R} \int \sqrt{ 1 + [f_{x}(x_{i},y_{i})]^{2} + [f_{y}(x_{i},y_{i})]^{2} } \: d A$$ $$= \int_{R} \int \sqrt{ 1+ 4x^{2} +1} \:d A$$ The bounds for \(R\) are \(0 \leqslant x \leqslant 1\) and \(x-1 \leqslant y \leqslant 1-x\), as shown in Figure 14.5.5. The integral becomes $$ S$$ $$= \int_{0}^{1} \int_{x-1}^{1-x} \sqrt{2+4x^{2}} \:dy \: dx$$ $$= \left. \int_{0}^{1} y\sqrt{2+4x^{2}} \right]_{x-1}^{1-x} \: dx$$ $$= \int_{0}^{1} \left[ (1-x)\sqrt{2+4x^{2}} - (x-1)\sqrt{2+4x^{2}} \right] \: dx$$ $$= \int_{0}^{1} \left( 2\sqrt{2+4x^{2}} - 2x\sqrt{2+4x^{2}} \right) \: dx \:\:\:\: \color{red}{ \text{Integration tables and Power Rule}}$$ $$= \left[ 2\sqrt{2+4x^{2}} + \ln(2x+\sqrt{2+4x^{2}})- \frac{(2+4x^{2})^{3/2}}{6} \right]_{0}^{1} $$ $$= \sqrt{6} + \ln(2+\sqrt{6}) - \sqrt{6} - \ln \sqrt{2} + \frac{1}{3} \sqrt{2} \approx 1.618$$

Example 14.5.3 Variables Changed to Polar Coordinates

Figure 14.5.6

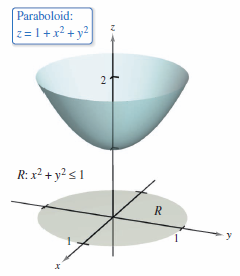
Find the surface area for the paraboloid \(z=1+x^{2}+y^{2}\) that lies above the unit circle, as shown in Figure 14.5.6. Solution Since \(f_{x}(x,y)=2x\) and \(f_{x}(x,y)=2y\), the area is $$S$$ $$= \int_{R} \int \sqrt{ 1 + [f_{x}(x_{i},y_{i})]^{2} + [f_{y}(x_{i},y_{i})]^{2} } \: d A$$ $$= \int_{R} \int \sqrt{ 1+ 4x^{2} +4y^{2}} \:d A$$ Let \(x= r \cos \theta\) and \(y=r \sin \theta\) to convert from cartesian to polar coordinates. The region \(R\) is bounded by \(0 \leqslant r \leqslant 1 \) and \(0 \leqslant \theta \leqslant 2 \pi\), producing $$S $$ $$=\int_{0}^{2 \pi} \int_{0}^{1} \sqrt{1+4r^{2}} \:r \: dr \: d\theta $$ $$= \int_{0}^{2 \pi} \left. \frac{1}{12} (1+4r^{2})^{3/2} \right]_{0}^{1} \: d\theta $$ $$= \int_{0}^{2 \pi} \frac{5 \sqrt{5}-1}{12} \: d\theta $$ $$= \left. \frac{5 \sqrt{5}-1}{12} \theta \right]_{0}^{2 \pi}$$ $$= \frac{\pi(5 \sqrt{5}-1)}{6} \approx 5.33$$

Example 14.5.4 Finding Surface Area

Figure 14.5.7

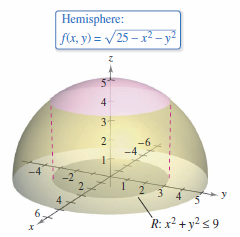
Find the surface area \(S\) for the hemisphere \(f(x,y)=\sqrt{25-x^{2}-y^{2}} \:\:\:\: \color{red}{ \text{Hemisphere }} \) that lies above the region \(R\) bounded by the circle \(x^{2}+y^{2} \leqslant 9\), as shown in Figure 14.5.7. Solution The first partial derivatives for \(f\) are $$f_{x}(x,y) = \frac{-x}{\sqrt{25-x^{2}-y^{2}}} $$ and $$f_{y}(x,y) = \frac{-y}{\sqrt{25-x^{2}-y^{2}}}. $$ Adding the formula for surface area produces $$ dS$$ $$= \sqrt{1+[f_{x}(x_{i},y_{i})]^{2} + [f_{y}(x_{i},y_{i})]^{2}} \: d A$$ $$= \sqrt{1+\left( \frac{-x}{\sqrt{25-x^{2}-y^{2}}}\right)^{2} +\left( \frac{-y}{\sqrt{25-x^{2}-y^{2}}}\right)^{2} } \: dA$$ $$= \frac{5}{\sqrt{25-x^{2}-y^{2}}} \: dA. $$ The surface area is $$S = \int_{R} \int \frac{5}{\sqrt{25-x^{2}-y^{2}}} \: dA. $$ Convert to polar coordinates by letting \(x= r \cos \theta\) and \(y=r \sin \theta\). The region \(R\) is bounded by \(0 \leqslant r \leqslant 3\) and \(0 \leqslant \theta \leqslant 2 \pi\), this produces $$S $$ $$= \int_{0}^{2 \pi} \int_{0}^{3} \frac{5}{\sqrt{25-x^{2}-y^{2}}} \:r \: dr \: d\theta$$ $$= 5 \left. \int_{0}^{2 \pi} - \sqrt{25-x^{2}-y^{2}} \right]_{0}^{3} \: d\theta $$ $$=5 \int_{0}^{2 \pi} \: d \theta = 10 \pi $$

Figure 14.5.8

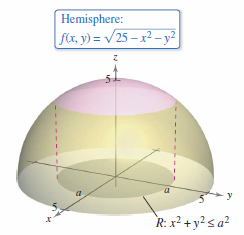
Example 14.5.4 can be extended to find the surface area for a sphere by using the region \(R\) bounded by the circle \(x^{2}+y^{2} \leqslant a^{2}\), where \( 0 < a < 5 \), as shown in Figure 14.5.8. The surface area for the hemisphere above the \(xy\)-plane is \( f(x,y)=\sqrt{25-x^{2}-y^{2}}.\) This produces $$S $$ $$= \int_{R} \int \frac{5}{\sqrt{25-x^{2}-y^{2}}} \: dA$$ $$= \int_{0}^{2 \pi} \int_{0}^{a} \frac{5}{\sqrt{25-r^{2}}} \: r \: dr \: d \theta$$ \(=10 \pi (5-\sqrt{25-a^{2}}). \) Taking the limit as \(a\) approaches 5 and doubling the result yields the total area at \(100\pi\). The surface area for a sphere with radius \(r\) is \(S=4\pi r^{2}\).

Example 14.5.5 Approximating Surface Area by Simpson’s Rule[1]

Figure 14.5.9 Figure 14.5.10

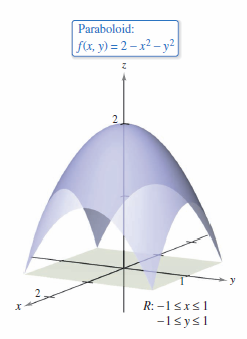
Find the surface area for the paraboloid \(f(x,y)= 2-x^{2}-y^{2} \:\:\:\: \color{red}{ \text{Paraboloid}} \) that lies above the square region bounded by \(-1 \leqslant x \leqslant 1 \) and \(-1 \leqslant y \leqslant 1\), as shown in Figure 14.5.9. 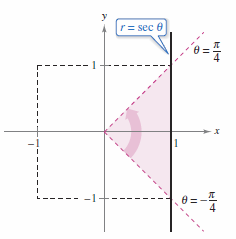Solution Using the partial derivatives \(f_{x}(x,y) = -2x\) and \(f_{y}(x,y) = -2y\) produces $$ S$$ $$=\int_{R} \int \sqrt{ 1 + [f_{x}(x_{i},y_{i})]^{2} + [f_{y}(x_{i},y_{i})]^{2} } \: d A $$ $$= \int_{R} \int \sqrt{ 1 + (-2x)^{2} + (-2y)^{2} } \: d A $$ $$= \int_{R} \int \sqrt{ 1 + 4x^{2} + 4y^{2} } \: d A.$$ In polar coordinates, the line \(x=1\) is given by \(r \cos \theta = 1 \) or \(r = \sec \theta. \) One quarter of region \(R\) is bounded by \(0 \leqslant r \leqslant \sec \theta \) and $$ -\frac{\pi}{4} \leqslant \theta \leqslant \frac{\pi}{4}, $$ as shown in Figure 14.5.10. Letting \(x= r \sec \theta\) and \(y=r \sin \theta\) produces $$ \frac{1}{4} S $$ $$= \frac{1}{4} \int_{R} \int \sqrt{ 1 + 4x^{2} + 4y^{2} } \: d A$$ $$= \int_{-\pi/4}^{\pi/4} \int_{0}^{\sec \theta} \sqrt{ 1 + 4r^{2}} \:r \: dr \: d\theta$$ $$= \int_{-\pi/4}^{\pi/4} \left. \frac{1}{12} ( 1 + 4r^{2})^{3/2} \right]_{0}^{\sec \theta} \: d\theta$$ $$= \frac{1}{12} \int_{-\pi/4}^{\pi/4} [( 1 + 4 \sec^{2})^{3/2} - 1 ] \: d\theta .$$ Applying Simpson's Rule with \(n=10\) approximates the surface area to $$ S = \frac{1}{3} \int_{-\pi/4}^{\pi/4} [( 1 + 4 \sec^{2})^{3/2} - 1 ] \: d\theta \approx 7.450.$$

Internal Links

Parent Article: Calculus III 14 Multiple Integration