Calculus III 15.03 Conservative Vector Fields and Independent Path

Previous	Calculus III 15.02 Line Integrals
Next	Calculus III 15.04 Green’s Theorem

15.03 Conservative Vector Fields and Independent Path

• The Fundamental Theorem of Line Integrals
• Path Independent
• Conservation of Energy

The Fundamental Theorem of Line Integrals

The discussion in Section 15.2 pointed out that in a gravitational field the work done by gravity on an object moving between two points in the field is independent from the path taken by the object. The discussion is generalized here in the Fundamental Theorem of Line Integrals. Example 15.3.1 describes how a line integral with a conservative vector field is evaluated over three different paths.

Example 15.3.1 Line Integral for a Conservative Vector Field

Path for a Figure 15.3.1 Path for b Figure 15.3.2 Path for c Figure 15.3.3

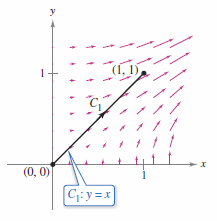
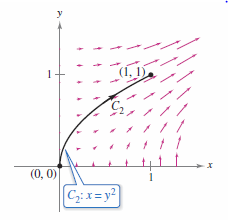
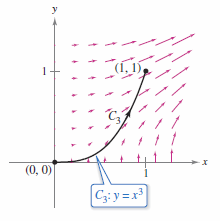
This example needs expansion and clarity. Find the work done by the force field $$\textbf{F}(x,y)= \frac{1}{2} xy\textbf{i}+\frac{1}{4}x^{2}\textbf{j}$$ on a particle that moves from \((0,0)\) to \((1,1)\) along each path, as shown in Figure 15.3.1, 15.3.2, and 15.3.3. a. \(C_{1}: \: y=x\:\:\:\:\) b. \(C_{2}: \: x=y^{2}\:\:\:\:\) c. \(C_{3}: \: y=x^{3}\) Solution Note that \(\textbf{F}\) is conservative because both the first partial derivatives are equal. $$\frac{\partial}{\partial y} \left[\frac{1}{2}xy \right]=\frac{1}{2}x \text{ and }\frac{\partial}{\partial x} \left[\frac{1}{4}x^{2} \right]=\frac{1}{2}x $$ a. Let \(\textbf{r}(t)=t\textbf{i}+t\textbf{j} \) for \(0\leqslant t \leqslant 1\), so that \(d\textbf{r}=(\textbf{i}+\textbf{j})\: dt\) and \(\textbf{F}(x,y)=\frac{1}{2}t^{2}\textbf{i}+\frac{1}{4}t^{2}\textbf{j}\). Back substitution produces the work done $$W$$ $$= \int_{C_{1}} \textbf{F} \cdot d\textbf{r}$$ $$=\int_{0}^{1} \frac{3}{4}t^{2}\:dt $$ $$= \left. \frac{1}{4}t^{3} \right]_{0}^{1} = \frac{1}{4},$$ as shown in Figure 15.3.1. b. Let \(\textbf{r}(t)=t\textbf{i}+\sqrt{t}\textbf{j} \) for \(0\leqslant t \leqslant 1\), so that $$d\textbf{r}=\left(\textbf{i}+\frac{1}{2\sqrt{t}}\textbf{j} \right)\: dt \text{ and } \textbf{F}(x,y)=\frac{1}{2}t^{3/2}\textbf{i}+\frac{1}{4}t^{2}\textbf{j}.$$ Back substitution produces the work done $$W$$ $$= \int_{C_{2}} \textbf{F} \cdot d\textbf{r}$$ $$=\int_{0}^{1} \frac{5}{8}t^{3/2}\:dt $$ $$= \left. \frac{1}{4}t^{5/2} \right]_{0}^{1} = \frac{1}{4},$$ as shown in Figure 15.3.2. c. Let \(\textbf{r}(t)=\frac{1}{2}t\textbf{i}+ \frac{1}{8}t^{3}\textbf{j} \) for \(0\leqslant t \leqslant 2\), so that $$d\textbf{r}=\left( \frac{1}{2}\textbf{i}+\frac{3}{8}t^{2}\textbf{j} \right)\: dt \text{ and } \textbf{F}(x,y)=\frac{1}{32}t^{4}\textbf{i}+\frac{1}{16}t^{2}\textbf{j}.$$ Back substitution produces the work done $$W$$ $$= \int_{C_{3}} \textbf{F} \cdot d\textbf{r}$$ $$=\int_{0}^{2} \frac{5}{128}t^{4}\:dt $$ $$= \left. \frac{1}{128}t^{5} \right]_{0}^{2} = \frac{1}{4},$$ as shown in Figure 15.3.3. The work done by the conservative vector field \(\textbf{F}\) is the same for each path.

Theorem 15.3.1 Fundamental Theorem of Line Integrals

Let \(C\) be a piecewise smooth curve lying in an open region \(R\) and given by

\(\textbf{r}(t)=x(t)\textbf{i}+y(t)\textbf{j}\), and \(a \leqslant t \leqslant b\).

If \(\textbf{F}(x,y)= M\textbf{i}+N\textbf{j}\) is conservative in \(R\), and \(M\) and \(N\) are continuous in \(R\), then

$$\int_{C} \textbf{F} \cdot d \textbf{r}= \int_{C} \nabla f \cdot \:d \textbf{r} = f(x(b),y(b)) - f(x(a),y(a))$$

where \(f\) is a potential function for \(\textbf{F}\). That is,

\(\textbf{F}(x,y) = \nabla f(x,y).\)

The three dimensions version is:
Let \(C\) be a piecewise smooth curve lying in an open region \(Q\) and given by

\(\textbf{r}(t)=x(t)\textbf{i}+y(t)\textbf{j}+z(t)\textbf{k}\), and \(a \leqslant t \leqslant b\).

If \(\textbf{F}(x,y,z)= M\textbf{i}+N\textbf{j}+P\textbf{k}\) is conservative and \(M\), \(N\) and \(N\) are continuous, then

$$\int_{C} \textbf{F} \cdot d \textbf{r}= \int_{C} \nabla f \cdot \:d \textbf{r} = f(x(b),y(b),z(b)) - f(x(a),y(a),z(a))$$

where \(\textbf{F}(x,y,z)= \nabla f(x,y,z).\)

If the vector field \(\textbf{F}\) is conservative, then the line integral between any two points is simply the difference between the potential function \(f\) at these points. This means that for any uniform force field the work done is the same between any two points no matter which path is followed.

Moving along a piecewise smooth curve \(C\) from \((x,y)\) to \((x_{1},y_{1})\) and back again produces zero work since work can be negative.

Proof This proof only addresses the smooth curve case. For the piecewise smooth curves case, the proof is carried out separately on each smooth portion.

Because

\(\textbf{F}(x,y)= \nabla f(x,y) = f_{x}(x,y)\textbf{i}+ f_{y}(x,y)\textbf{j}\)

if follows that

$$\int_{C} \textbf{F} \cdot \: d\textbf{r} $$	$$=\int_{a}^{b} \textbf{F} \cdot \frac{d\textbf{r}}{dt}\: dt$$
	$$=\int_{a}^{b} \left[ f_{x}(x,y)\frac{dx}{dt} + f_{y}(x,y)\frac{dy}{dt} \right] \: dt. $$
	$$=\int_{a}^{b} \frac{d}{dt}[f(x(t),y(t))] \: dt $$	Apply the Chain Rule
	\(= f(x(b),y(b)) - f(x(a),y(a)).\)	Apply the Fundamental Theorem of Calculus

Example 15.3.2 Using the Fundamental Theorem of Line Integrals in a Plane

Figure 15.3.4

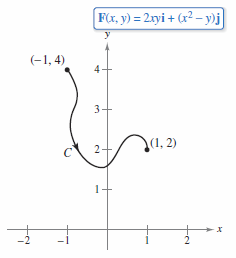
Evaluate $$ \int_{C} \textbf{F} \cdot \: d\textbf{r}, $$ where \(C\) is a piecewise smooth curve from \((-1,4)\) to \((1,2)\) and \(\textbf{F}(x,y) = 2xy\textbf{i}+(x^{2}-y)\textbf{j}\) as shown in Figure 15.3.4. Solution From Example 15.1.6 \(\textbf{F}\) is a gradient for \(f\), where $$f(x,y)=x^{2}y - \frac{1}{2}y^{2}+ K. $$ Therefore \(\textbf{F}\) is conservative and applying the Fundamental Theorem of Line Integrals produces $$\int_{C} \textbf{F} \cdot \: d\textbf{r} $$ \(=f(\color{red}{1},\color{red}{2})-f(\color{red}{-1},\color{red}{4}) \) $$= \left[ \color{red}{1}^{2}(\color{red}{2})-\frac{\color{red}{2}^{2}}{2}\right] - \left[(\color{red}{-1})^{2}(\color{red}{4})-\frac{\color{red}{4}^{2}}{2} \right] =4.$$ Note that \(K\) is eliminated by subtraction.

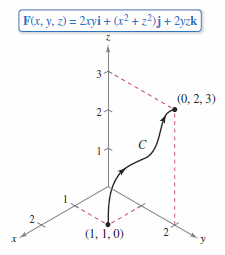
Example 15.3.3 Using the Fundamental Theorem of Line Integrals in Three Dimensions

Figure 15.3.5

Evaluate $$ \int_{C} \textbf{F} \cdot \: d\textbf{r}, $$ where \(C\) is a piecewise smooth curve from \((1,1,0)\) to \((0,2.3)\) and \(\textbf{F}(x,y,z) = 2xy\textbf{i}+(x^{2}+z^{2})\textbf{j}+2yz\textbf{k}\) as shown in Figure 15.3.5. Solution Example 15.1.8 showed that \(\textbf{F}\) is a gradient for \(f\), where \(f(x,y,z)=x^{2}y + yz^{2}+K.\) Therefore \(\textbf{F}\) is conservative. Applying the Fundamental Theorem of Line Integrals produces $$\int_{C} \textbf{F} \cdot \: d\textbf{r}$$ \(=f(\color{red}{0},\color{red}{2},\color{red}{3})-f(\color{red}{1},\color{red}{1},\color{red}{0}) \) \(=[(\color{red}{0})^{2}(\color{red}{2})+(\color{red}{2})(\color{red}{3})^{2}]-[(\color{red}{1})^{2}(\color{red}{1})+(\color{red}{1})(\color{red}{0})^{2}] =17\)

Path Independent

Figure 15.3.6

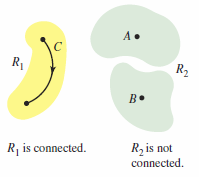
Th line integral $$\int_{C} \textbf{F} \cdot \: d\textbf{r}$$ is path independent in a region with a uniform force field for every piecewise smooth curve \(C\) from one fixed point to another.. As was shown in Example 15.3.1. This is derived from Fundamental Theorem of Line Integrals where \(\textbf{F}\) is continuous and conservative over an open region. A region in the plane, or three dimensions, is connected when any two points in the region can be joined by a piecewise smooth curve lying entirely within the region, as shown in Figure 15.3.6. In open region that are connected, the independent path

Theorem 15.3.2 Path Independent and Conservative Vector Fields

Region \(R\) for Theorem 15.3.2 Figure 15.3.7

If \(\textbf{F}\) is continuous on an open connected region, then the line integral $$\int_{C} \textbf{F} \cdot \: d\textbf{r}$$ is path independent if and only if \(\textbf{F}\) is conservative. Proof If \(\textbf{F}\) is conservative, then, by the Fundamental Theorem of Line Integrals, the line integral is path independent. Now establish the converse for a plane region \(R\). Let \(\textbf{F}(x,y) = M \textbf{i}+N\textbf{j}\) and let \((x_{0},y_{0})\) be a fixed point in \(R\). For any point \((x,y)\) in \(R\), choose a piecewise smooth curve \(C\) running from \((x_{0},y_{0})\) to \((x,y)\), and define \(f\) by \(f(x,y)\) $$= \int_{C} \textbf{F} \cdot \: d\textbf{r}$$ $$=\int_{C} M\:dx + N\:dy. 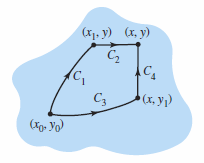$$ The curve \(C\) is guaranteed to exist in \(R\) because \(R\) is connected. The proving that \(f\) is a potential function for \(\textbf{F}\) is done by considering two different paths from \((x_{0},y_{0})\) to \((x,y)\). The first path choose a point \((x_{1},y)\) in \(R\) such that \(x \ne x_{1}\). This is possible because \(R\) is open. Then choose \(C_{1}\) and \(C_{2}\), as shown in Figure 15.3.7. Using path independence it follows that \(f(x,y)\) $$=\int_{C} M\:dx + N\:dy $$ $$=\int_{C_{1}} M\:dx + N\:dy + \int_{C_{2}} M\:dx + N\:dy.$$ $$=g(y) + \int_{C_{2}} M\:dx. \:\:\:\: \color{red}{C_{1} \text{ does not depend on }x \text{ and } dy=0} $$ The partial derivative for \(f\) with respect to \(x\) is \(f_{x}(x,y)=M.\) For the second path choose a point \((x_{1},y)\). Using reasoning similar to that used for the first path concludes with \(f_{y}(x,y)=N.\) Therefore, \(\nabla f(x,y) \) \(= f_{x}(x,y)\textbf{i} + f_{y}(x,y)\textbf{j} \) \(= M\textbf{i} + N\textbf{j}\) \(=\textbf{F}(x,y) \) and if follows that \(\textbf{F}\) is conservative.

Example 15.3.4 Finding Work in a Conservative Force Field

Find the force field given by

\(\textbf{F}(x,y)=e^{x} \cos y\textbf{i} - e^{x} \sin y\textbf{j} + 2\textbf{k} \)

show that

$$\int_{C} \textbf{F} \cdot \: d\textbf{r}$$

is path independent, and calculate the work done by \(\textbf{F}\) on an object moving along a curve \(C\) from \((0,\pi/2,1)\) to \((1,\pi,3)\).
Solution Expressing the force field in the form

\(\textbf{F}(x,y,z)=M\textbf{i}+N\textbf{j}+P\textbf{k}\)

yields \(M=e^{x} \cos y\), \(N=-e^{x} \sin y\), and \(P=2\). The partial derivatives yield

$$\frac{\partial P}{\partial y} $$	\(=0\)	$$=\frac{\partial N}{\partial z} $$
$$\frac{\partial P}{\partial x} $$	\(=0\)	$$=\frac{\partial M}{\partial z} $$
and
$$\frac{\partial N}{\partial x} $$	\(=-e^{x} \sin y\)	$$= \frac{\partial M}{\partial y}.$$

Therefore, \(\textbf{F}\) is conservative. If \(f\)is a potential function for \(\textbf{F}\), then

\(f_{x}(x,y,z)\)	\(= e^{x} \cos y\)
\(f_{y}(x,y,z)\)	\(=-e^{x} \sin y \)
and
\(f_{z}(x,y,z)\)	\(= 2.\)

Integrating with respect to \(x\), \(y\), and \(z\) separately yields

\(f(x,y,z)\)	$$=\int f_{x}(x,y,z) \: dx $$	$$=\int e^{x} \cos y \: dx =e^{x} \cos y+g(y,z) $$
\(f(x,y,z)\)	$$=\int f_{y}(x,y,z) \: dy $$	$$=\int -e^{x} \sin y \: dy = e^{x} \cos y +h(x,z) $$
and
\(f(x,y,z)\)	$$=\int f_{z}(x,y,z) \: dz $$	$$=\int 2 \: dz=2z+k(x,y).$$

Combining all three \(f(x,y,z)\) versions produces

\(f(x,y,z)= e^{x} \cos y +2z + K.\)

Therefore, the work done by \(\textbf{F}\) along any curve \(C\) from \((0,\pi/2,1)\) to \((1,\pi,3)\) is

\(W\)	$$=\int_{C} \textbf{F} \cdot \: d\textbf{r} $$
	$$=\left[ \vphantom{\frac{1}{2}} e^{x} \cos y +2z \right]_{(0,\pi/2,1)}^{(1,\pi,3)} $$
	\(=(-e+6)-(0+2) = 4-e. \)

Theorem 15.3.3 Equivalent Conditions

Let \(\textbf{F}(x,y,z) = M\textbf{i}+N\textbf{j}+P\textbf{k}\) have continuous first partial derivatives in an open connected region \(R\), and let \(C\) be a piecewise smooth curve in \(R\). The conditions below are equivalent

1.	\(\textbf{F}\) is conservative. That is, \(\textbf{F} = \nabla f\) for some function \(f\).
2.	\(\int_{C} \textbf{F} \cdot d \textbf{r} \) is path independent.
3.	\(\int_{C} \textbf{F} \cdot d \textbf{r}=0 \) for every closed curve \(C\) in \(R\).

A curve \(C\) given by \(\textbf{r}(t)\) for \( a \leqslant t \leqslant b\) is closed when \(\textbf{r}(a)=\textbf{r}(b)\). By the Fundamental Theorem of Line Integrals, therefore, if \(\textbf{F}\) is continuous and conservative on an open region \(R\), then the line integral over every closed curve \(C\) is 0.

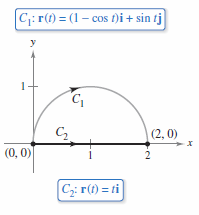
Example 15.3.5 Evaluating a Line Integral

Figure 15.3.8

Evaluate $$\int_{C_{1}} \textbf{F} \cdot d \textbf{r},$$ where \(\textbf{F}(x,y)= (y^{3}+1)\textbf{i}+(3xy^{2}+1)\textbf{j}\) and \(C_{1}\) is the semicircular path from \((0,0)\) to \((2,0)\), as shown in Figure 15.3.8. Solution There are three possible options. a. The vector method described in Section 15.2 can be applied to evaluate a line integral along the given curve. Use the parametrization \(\textbf{r}(t)=(1-\cos t)\textbf{i}+\sin t\textbf{j}\), where \(0 \leqslant t \leqslant \pi\). This produces \(d\textbf{r} = \textbf{r}^{\prime}(t)\: dt=(\sin t \textbf{i}+\cos t\textbf{j}\: dt\) and $$ \int_{C_{1}} \textbf{F} \cdot d\textbf{r} = \int_{0}^{\pi} (\sin t + \sin^{4}t+\cos t+3 \sin^{2}t \cos t-3\sin^{2}t \cos^{2}t) \: dt.$$ The integration complexity alone eliminates this option. b. Find a potential function and evaluate the line integral by the Fundamental Theorem of Line Integrals. Using the technique demonstrated in Example 15.3.4, the potential function is \(f(x,y)=xy^{2}+x+y+K\), and, by the Fundamental Theorem, $$W=\int_{C_{1}} \textbf{F} \cdot d\textbf{r} = f(2,0)-f(0,0)=2.$$ A much easier option. c. Because \(\textbf{F}\) is conservative, the line integral's value is path independent. Thus, replace the semicircular path with a simpler path. Choose the straight-line path \(C_{2}\) from \((0,0)\) to \((2,0)\). Let \(\textbf{r}(t)=t\textbf{i}\) for \(0 \leqslant t \leqslant 2\), so that \(d\textbf{r}=\textbf{i}\:dt\) and \(\textbf{F}(x,y)=\textbf{i}+\textbf{j}\). This produces the integral $$\int_{C_{1}} \textbf{F} \cdot d \textbf{r}=\int_{C_{2}} \textbf{F} \cdot d \textbf{r}=\int_{0}^{2} 1 \:dt=\left.\vphantom{\frac{1}{2}} t \right]_{0}^{2} =2.$$ The easiest option among the three.

Conservation of Energy

The work done by \(\textbf{F}\) along \(C\). Figure 15.3.9

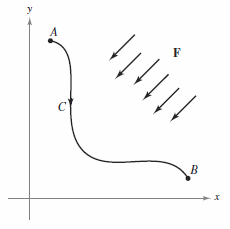
In 1840, the English physicist Michael Faraday[1] wrote, “Nowhere is there a pure creation or production of power without a corresponding exhaustion of something to supply it.” This statement represents the first expression for law in physics — the Law of Conservation of Energy. In modern terminology, the law is stated as follows: In a conservative force field, the sum of the potential and kinetic energies of an object remains constant from point to point. The Fundamental Theorem of Line Integrals is derived from this law. From physics, the kinetic energy for a particle with mass \(m\) and speed \(v\) is $$k=\frac{1}{2}mv^{2}.$$     Kinetic energy The potential energy \(p\) for a particle at point \((x,y,z)\) in a conservative vector field \(\textbf{F}\) is defined as \(p(x,y,z)=-f(x,y,z)\), where \(f\) is the potential function for \(\textbf{F}\). Therefore, the work done by \(\textbf{F}\) along a smooth curve \(C\) from \(A\) to \(B\) is $$W $$ $$=\int_{C} \textbf{F} \cdot \: d\textbf{r}$$ $$=\left.\vphantom{\frac{1}{2}} f(x,y,z) \right]_{A}^{B}$$ $$=-\left.\vphantom{\frac{1}{2}} p(x,y,z) \right]_{A}^{B} = p(A)-p(B), $$ as shown in Figure 15.3.9. The work \(W\) is equal to the difference in the potential energies for \(A\) and \(B\). Suppose that \(\textbf{r}(t)\) is the position vector for a particle moving along \(C\) from \(A=\textbf{r}(a)\) to \(B=\textbf{r}(b)\). At any time \(t\), the particle's velocity, acceleration, and speed are \(\textbf{v}(t)=\textbf{r}^{\prime}(t)\), \(\textbf{a}(t)=\textbf{r}^{\prime \prime}(t)\), and \(v(t)=\|\textbf{v}(t)\|\), respectively. Applying Newton's Second Law of Motion[2] yields, \(\textbf{F}=m\textbf{a}(t)=m(\textbf{v}^{\prime}(t))\), and the work done by \(\textbf{F}\) is $$W $$ $$=\int_{C} \textbf{F} \cdot \: d\textbf{r}$$ $$=\int_{a}^{b} \textbf{F} \cdot \textbf{r}^{\prime}(t) \: dt $$ $$=\int_{a}^{b} \textbf{F} \cdot \textbf{v}(t) \: dt $$ $$=\int_{a}^{b} [m\textbf{v}^{\prime}(t)] \cdot \textbf{v}(t) \: dt$$ $$=\int_{a}^{b} m[\textbf{v}^{\prime}(t) \cdot \textbf{v}(t)] \: dt $$ $$= \frac{m}{2}\int_{a}^{b} \frac{d}{dt}[\textbf{v}(t) \cdot \textbf{v}(t)] \: dt $$ $$= \frac{m}{2}\int_{a}^{b} \frac{d}{dt}[\| \textbf{v}(t) \| ^{2}] \: dt $$ $$= \frac{m}{2} \left[ \vphantom{\frac{1}{2}} \| \textbf{v}(t) \| ^{2} \right]_{a}^{b} $$ $$= \frac{m}{2} \left[ \vphantom{\frac{1}{2}} [ v(t) ]^{2} \right]_{a}^{b} $$ $$=\frac{1}{2} m [ v(b) ]^{2} - \frac{1}{2} m [ v(a) ]^{2} = k(B)-k(A).$$ Equating these two results for \(W\) produces \( p(A)-p(B)\) \(= k(B)-k(A)\) \( p(A)+k(A)\) \(= p(B)+k(B)\) which implies that the sum for the potential and kinetic energies remains constant from point to point.

Internal Links

Parent Article: Calculus III 15 Vector Analysis