Calculus III Advanced (Course) (11.1) (Homework)

Section 11.1 Homework

From Calculus 10e by Larson and Edwards, p. 755. Exercises 8, 28, 36, 50, 84.

Exercise 11.1.8 Show that vectors u and v are equivalent

u (-4,-1), (11,-4)
v (10,13), (25,10)
Solution Since vectors are line segments the length, magnitude, and slope, direction must match.

Distance	\(=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}} \)
u	\(= \sqrt{(-4-11)^{2}+(-1-(-4))^{2}} \)
	\(= \sqrt{(-15)^{2}+(3)^{2}} = \sqrt{ 234 } \)
v	\(= \sqrt{(10-25)^{2}+(13-10)^{2}} \)
	\(= \sqrt{(-15)^{2}+(3)^{2}} = \sqrt{ 234 } \)

Slope	$$= \frac{x_{2}-x_{1}}{y_{2}-y_{1}} $$
u	$$= \frac{-1-(-4)}{-4-11} $$
	$$ = \frac{3}{-15} = - \frac{1}{5} $$
v	$$= \frac{13-10}{10-25} $$
	$$ = \frac{3}{-15} = - \frac{1}{5} $$

The vectors u and v are equivalent because they have the same length and slope.

Exercise 11.1.28 Find the Terminal Point

Find a terminal point, given \( \textbf{v}= \left \langle 4,-9 \right \rangle \); Initial point: (5,3).
The terminal point is:

\( (4 + 5, -9 + 3) = (9,-6) \)

Exercise 11.1.36 Find the unit vector in v's direction and verify that it has length 1

Let \( \textbf{v}= \left \langle -5,15 \right \rangle \).

$$ \frac{\textbf{v}}{\left \| \textbf{v} \right \|} $$	$$= \frac{ \left \langle -5,15 \right \rangle }{\sqrt{(-5)^{2}+(15)^{2}}}$$
	$$=\frac{1}{\sqrt{250}}\left \langle -5,15 \right \rangle $$
	$$= \left \langle \frac{-5}{\sqrt{250}},\frac{15}{\sqrt{250}} \right \rangle$$
Substitute this into the proof for Theorem 11.1.2 yields.
	$$= \sqrt{ \left(\frac{-5}{\sqrt{250}}\right)^{2} + \left(\frac{15}{\sqrt{250}}\right)^{2} }$$
	$$= \sqrt{ \frac{25}{250}+\frac{225}{250}} $$
	$$= \sqrt{\frac{250}{250}} = 1$$

Exercise 11.1.50 Find the component form for v, given its magnitude and angle the positive \(x\)-axis.

Let \(\left \| \textbf{v} \right \| = 3\) and \(\theta = 120^{\circ} \).

Because the angle between v and the positive \(x\)-axis is \(\theta = 2\pi /3 \) the vector can be described as

\(\textbf{v} \)	\(=\left \| \textbf{v} \right \|\cos \theta\:\textbf{i} + \left \| \textbf{v} \right \| \sin \theta \:\textbf{j}\).
	$$=3 \cos \frac{2\pi}{3}\textbf{i} + 3 \sin \frac{2\pi}{3}\textbf{j} $$
	$$= -\frac{3}{2}\textbf{i} + \frac{3\sqrt{3}}{2}\textbf{j} $$

Exercise 11.1.84 Navigation

Figure 11.1 Figure 11.2

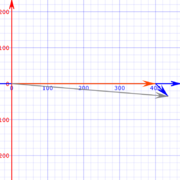
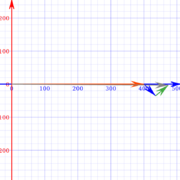
A plane flies at a 400 mph constant ground speed due east, 90°. A 50-mile-per-hour wind hits the plane from the northwest, 135°. Find the airspeed and compass direction that will allow the plane to maintain its ground speed and eastward direction. Let \( \textbf{v}_{1}\) be the airplane's vector. Let \( \textbf{v}_{2}\) be the wind's vector. Let \( \textbf{v}_{3}\) be the combined vectors that represent the airplane's new course. Let \( \textbf{v}_{4}\) be the airplane's corrected course. \( \textbf{v}_{1}\) \(= 400 \cos( 90^{\circ} ), 400 \sin(90^{\circ})\) \(= 400 * 1 , 400 * 0\) \(= (400, 0)\) \( \textbf{v}_{2}\) \(= 50 \cos( 135^{\circ} ), 50 \sin(135^{\circ})\) $$= 50 \frac{\sqrt{2}}{2} , 50 -\frac{\sqrt{2}}{2}$$ \(= 25 \sqrt{2} , 25 -\sqrt{2}\) \(= 35.335, -35.335\) \( \textbf{v}_{3}\) \(= 400 + 35.335, 0^{\circ} + (-35.335^{\circ})\) \(= 435.335 , -35.335^{\circ}\) The airplane's new course is 125.335°, at \(\approx \) 435.335 mph, as shown in Figure 11.1. Remember, north is 0°, east is 90°, so the new course is 90° + 35.355° or 125.335°. Now \( \textbf{v}_{3} - \textbf{v}_{1} \) to get the corrected course, \( \textbf{v}_{4}\) \( \textbf{v}_{4}\) \(= 435.335 - 400 , -35.335^{\circ} - 90^{\circ}\) \(= 35.355, -125.355^{\circ} \) As shown in Figure 11.2.

Internal Links

Parent Article: Calculus III Advanced (Course)