Calculus III Advanced (Course) (13.10) (Homework)

Section 13.10 Homework

From Calculus 10e by Larson and Edwards, p. 958. Exercises 6, 24, 34, 46.

Exercise 13.10.6 Using Lagrange Multipliers

Use Lagrange multipliers to find the indicated extrema, assuming that \(x >0\) and \(y>0\).
Maximize \(f(x,y)=3x+y+10\)
Constraint \(x^{2}y=6\)
Solution Let

\( g(x,y) = x^{2}y-6=0\)

and

\( \nabla f(x,y) = 3\textbf{i} + \textbf{j} \)

and

\( \lambda \nabla g(x,y) = \lambda 2xy, \lambda x^{2} \)

so

3	\(= \lambda 2xy\)
1	\(= \lambda x^{2} \)
\(x^{2}y\)	\(=6. \)

Solve for \(y\).

3	\(= 3x^{2}\)
\(2xy\)	\(= 3x^{2}\)
\(y\)	\(= 3x/2 \)

Plug that into the constraint.

$$ \frac{ 3x^{3}}{2}$$	\(= 6 \)
\(3x^{3}\)	\(= 12 \)
\(x^{3} \)	\(= 4 \)
\(x \)	\(= \sqrt[3]{4} \)

Then \(y=1.5 \times \sqrt[3]{4}\) and \( \lambda = 4^{-2/3} \). The maximum value for \(f(x,y)\) is equal to

\(f(\sqrt[3]{4}, 1.5 \times \sqrt[3]{4}) = 4.5 \times \sqrt[3]{4} + 10.\)

Exercise 13.10.24 Finding Minimum Distance

Use Lagrange multipliers to find the minimum distance from the curve or surface to the indicated point. (Hint: To simplify the computations, minimize the square of the distance.)

Circle: \((x-4)^{2}+y^{2}=4\)
Point: \((0,10)\)
Solution Let \((0,10)\) be \(x_{2}\) in the distance formula. This makes the equation

\( f(x,y)=x^{2}+(y-10)^{2}\)

and the constraint

\((x-4)^{2}+y^{2}=4\).

This makes

\( \nabla f(x,y) = 2x\textbf{i} + 2(y-10)\textbf{j} \)

and

\( \lambda \nabla g(x,y) = \lambda 2(x-4) + \lambda 2y. \)

This produces the equations

\(2x\)	\(= \lambda 2(x-4) \)
\(2(y-10) \)	\(= \lambda 2y\)
\((x-4)^{2}+y^{2} \)	\(= 4\)

which yield

\(x\)	\(= \frac{4 \lambda}{\lambda -1} \)
\(y\)	\(= -\frac{10}{\lambda -1} \)

Plug this into the formula yields

$$ \left( \frac{4 \lambda}{\lambda -1} -4\right)^{2} + \frac{100}{(\lambda -1)^{2}} =4 \rightarrow (\lambda -1)^{2} $$

\( \lambda \)	\(= 1 \pm \sqrt{29} \:\:\:\: \) two solutions.
\( \lambda \)	\(= 4(\sqrt{29}+1)^{2} \)
\( \lambda \)	\(= 4(\sqrt{29}-1)^{2}\)

The 2nd value is smaller, taking the square, to match the distance formula, yields \(2(\sqrt{29}-1)\).

Exercise 13.10.34 Using Lagrange Multipliers

Find three positive integers \(x\), \(y\), and \(z\) that satisfy the given conditions.

The sum is 32, and \(P=xy^{2}z\).
Solution Assume \(\lambda \), \(x\), \(y\), and \(z\) are \(>0\). Let

\(P = xy^{2}z\)

and the constraint be

\( g(x,y,z)= x+y+z = 32 = 0\).

\(\nabla P \)	\(= y^{2}z\textbf{i} + 2xyz\textbf{j} + xy^{2}\textbf{k} \)
\(\lambda \)	\(= y^{2}z\)
\(\lambda \)	\(= 2xyz\)
\(\lambda \)	\(= xy^{2}\)
\(x+y+z\)	\(= 32\)

Reducing the equations produces

\(y\)	\(=2x \)
\(y\)	\(=2z \)
so
\(x=z=y/2\)
plug this into the constraint equation yields
\(2y\)	\(=32\)
therefore
\(y\)	\(=16\)
\(x=z\)	\(=8\)

The maximum value for \(P\) is

\( P(8,16,8) = 16384\).

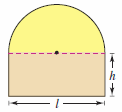
Exercise 13.10.46 Area and Perimeter

Figure 1

A semicircle is atop a rectangle, as shown in Figure 1. When the area is fixed and the perimeter is a minimum, or when the perimeter is fixed and the area is a maximum, use Lagrange multipliers to verify that the length of the rectangle is twice its height. Solution Let \(l=length\), \(h=height\), \(A^{\prime}=area\), and \(P^{\prime}=perimeter\). Therefore, the area is $$ A(l,h)= lh+ \frac {\pi \left( \frac{l}{2} \right)^{2}}{2} =A^{\prime}. $$ The perimeter is $$P(l,h) = l+2h + \pi \frac{l}{2} = P^{\prime}$$ Part 1 The area is fixed and minimize perimeter. $$ f(l,h) = l+2h + \pi \frac{l}{2} $$ $$ g(l,h) = lh+ \frac{\pi l^{2}}{8} -A^{\prime} = 0$$ \( \nabla f(l,h) = (\pi/2 +1)\textbf{i} + 2\textbf{j} \) \( \lambda \nabla g(l,h) = \lambda(h+\frac{\pi l}{4})\textbf{i} + \lambda l \textbf{j} \) This produces the following equation system. \( (\pi/2 +1)\) \(= \lambda(h+\frac{\pi l}{4})\) \(2\) \(= \lambda l\) \( lh+ \frac{\pi l^{2}}{8} \) \(= A^{\prime}\) Plug \( l = 2 / \lambda \) into the first equation yields. \( \frac{\pi}{2} +1\) $$= \lambda(h+\frac{\pi 2/\lambda }{4}) $$ \( \frac{\pi}{2} +1\) $$= \lambda h+ \lambda \frac{\pi 2/\lambda }{4} $$ \( \frac{\pi}{2} +1\) $$= \lambda h+ \frac{\pi}{2} $$ \( 1\) $$= \lambda h $$ Therefore, \(h=2l\). Part 2 The perimeter is fixed and minimize area. $$ f(l,h) = lh+ \frac{\pi l^{2}}{8}$$ $$ g(l,h) = l+2h + \pi \frac{l}{2} - P^{\prime} = 0$$ \( \nabla f(l,h) = (h+\frac{\pi l}{4})\textbf{i} +l\textbf{j} \) \( \lambda \nabla g(l,h) = \lambda(\pi/2 +1)\textbf{i} + \lambda 2\textbf{j}\) This produces the following equation system. \( (h+\frac{\pi l}{4}) \) \(= \lambda(\pi/2 +1)\) \(l\) \(= \lambda 2 \) \( lh+ \frac{\pi l^{2}}{8} \) \(= A^{\prime}\) Plug \(l/2 = \lambda \) into the first equation yields \( h+\frac{\pi l}{4} \) \(=\frac{l}{2}(\pi/2 +1) \) \( h+\frac{\pi l}{4} \) \(= \frac{\pi l}{4} + \frac{l}{2} \) \(h\) \(= \frac{l}{2} \) Therefore, \(h= l/2\).

Internal Links

Parent Article: Calculus III Advanced (Course)