Calculus III Advanced (Course) (13.6) (Homework)

Section 13.6 Homework

From Calculus 10e by Larson and Edwards, p. 924. Exercises 2, 24, 36, 52, 61

Exercise 13.6.2 Finding a Directional Derivative

Use Theorem 13.6.1 to find the directional derivative for the function at \(P\) in the unit vector \( \textbf{u} = \cos \theta \textbf{i} + \sin \theta \textbf{j} \)'s direction.

$$ f(x,y) = \frac{y}{x+y} , \: P(3,0), \: \theta = - \frac{\pi}{6} $$

Solution

$$ f_{x}(x,y) = -\frac{y}{(x+y)^{2}} $$

and

$$ f_{y}(x,y) = \frac{x}{(x+y)^{2}} $$

$$D_{\textbf{u}} (3,0) = -\frac{0}{(3+0)^{2}} \cos \left(- \frac{\pi}{6} \right) + \frac{3}{(3+0)^{2}} \sin \left( - \frac{\pi}{6} \right) = \left( \frac{1}{3} \right) \left( -\frac{1}{2} \right) = - \frac{1}{6}$$

Exercise 13.6.24 Finding a Directional Derivative Using the Gradient

Use the gradient to find the directional derivative for the function at \(P\) in the direction of \(Q\).

\( f(x,y) = 3x^{2}-y^{2}+4\), \(P(-1,4)\), \(Q(3,6)\)

Solution First, find the gradient

\( f_{x}(x,y) = 6x\)

and

\( f_{y}(x,y) = -2y\)

\(\nabla f(x,y) = 6x\textbf{i} -2y \textbf{j} \)

at the point \(P(-1,4)\)

\(\nabla f(x,y) = -6\textbf{i} -8 \textbf{j} \)

Now find the unit vector.

\( \vec{PQ} = (3+1)\textbf{i} + (6-4)\textbf{j} = 4 \textbf{i} + 2\textbf{j} \)

$$\textbf{u} = \frac{4}{\sqrt{20}} \textbf{i} + \frac{2}{\sqrt{20}}\textbf{j} $$

$$ D_{\textbf{u}}(-1,4) = (-6\textbf{i} -8 \textbf{j} ) \cdot \left( \frac{4}{\sqrt{20}} \textbf{i} + \frac{2}{\sqrt{20}}\textbf{j} \right) = -\frac{4}{\sqrt{5}} $$

Exercise 13.6.36 Using Gradient Properties

Find the gradient for the function and the maximum value for the directional derivative at the given point.

\(f(x,y,z) = xe^{yz}, \: (2,0,-4)\)

Solution Find the partials

\( f_{x}(x,y,z) = e^{yz} \)

\( f_{y}(x,y,z) = zxe^{yz} \)

\( f_{z}(x,y,z) = yxe^{yz} \)

\( \nabla f(x,y,z) = e^{yz}\textbf{i} + zxe^{yz} \textbf{j} + yxe^{yz} \textbf{k} \)

\( \nabla f(2,0,-4) = e^{(0)(-4)}\textbf{i} + (-4)(2)e^{(0)(-4)} \textbf{j} + (0)(2)e^{(0)(-4)} \textbf{k}= 1\textbf{i} -8 \textbf{j} + 0\textbf{k} = \sqrt{65} \)

Exercise 13.6.52 Using a Function

(a) Find the gradient for the function at \(P\).
(b) Find a unit normal vector to the level curve at \(f(x,y) = c\) at \(P\).
(c) Find the tangent line to the level curve \(f(x,y) = c\) at \(P\).
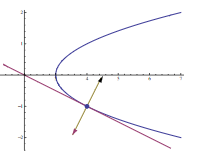
(d) Sketch the level curve, the unit normal vector, and the tangent line in the \(xy\)-plane.

\(f(x,y) = x-y^{2} \), \(c=3\), and \(P(4,-1)\)

Solution
(a) First, find the partials

\(f_{x}(x,y) = 1\)

\(f_{y}(x,y) = -2y\)

yields

\( \nabla f(x,y) = \textbf{i} -2y \textbf{j} \:\:\:\: \)Gradient

\( \nabla f(4,-1) = \textbf{i} -2(-1) \textbf{j} = \textbf{i} +2 \textbf{j} = \langle 1,2 \rangle \:\:\:\: \)Gradient at \(P\)

(b)

$$ \textbf{u} = \frac{1}{\sqrt{5}} \textbf{i} + \frac{2}{\sqrt{5}}\textbf{j} $$

(c)

\( \langle 1,2 \rangle \cdot \langle x-4, y+1 \rangle = 0 \rightarrow x+2y=2 \)

(d)

Figure 1

Exercise 13.6.61 Topography

A mountain surface is described by the equation

\(h(x,y) = 5000 - 0.001x^{2} - 0.004y^{2} \)

A mountain climber is at the point \((500,300,4390)\). In what direction should the climber move in order to ascend at the greatest rate?
Solution Find the increase at the maximum rate.

\( \nabla h(x,y,z) \)	\(= h_{x}(x,y,z)\textbf{i} + h_{y}(x,y,z)\textbf{j} +h_{z}(x,y,z)\textbf{k} \)
	\(= -0.002x\textbf{i} -0.008y\textbf{j}\)
\( \nabla h(500,300,4390) \)	\(= -0.002(500)\textbf{i} -0.008(300)\textbf{j}\)
	\( = -1\textbf{i} -2.4\textbf{j} = \langle -1, -2.4 \rangle \)

Gradient vector is

$$\textbf{u} = \frac{\nabla h}{ \| \nabla h \|} = \frac{\langle -1, -2.4 \rangle}{ \sqrt{6.76}} \approx \langle -0.38, -0.92 \rangle $$

Internal Links

Parent Article: Calculus III Advanced (Course)