Calculus III Advanced (Course) (13.7) (Homework)
Contents
Section 13.7 Homework
From Calculus 10e by Larson and Edwards, p. 933. Exercises 10, 18, 24, 42.
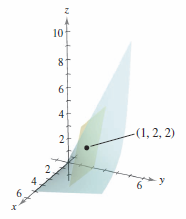
Exercise 13.7.10 Finding an Equation for a Tangent Plane
Find an equation for the tangent plane to the surface at the given point.
- $$f(x,y)= \frac{y}{x}, \: (1,2,2) $$
Solution Write the surface as
- $$g(x,y,z) = \frac{y}{x}- z = 0. $$
- \( g(x,y,z) = \frac{y}{x} - z\)
- \( f_{x}(x,y,z) =- \frac{y}{x^{2}} \)
- \( f_{y}(x,y,z) = \frac{1}{x} \)
- \( f_{z}(x,y,z) = -1 \)
At the point \((1,2,2)\) the partial derivatives are
- \( f_{x}(1,2,2) =- \frac{2}{1^{2}} = -2 \)
- \( f_{y}(1,2,2) = \frac{1}{x} = 1 \)
- \( f_{z}(1,2,2) = -1 \)
An equation for the tangent plan at \((1,2,2)\) is
| \( 0 \) | \(= f_{x}(1,2,2)(x-1) + f_{y}(1,2,2)(y-2) + f_{z}(1,2,2)(z-2)\) |
| \(= -2(x-1) + (1)(y-2)+ (-1)(z-2)\) | |
| \(= -2x+2 +y-2-z+2 \) | |
| \(= -2x+y-z +2 \) | |
| \( 2x-y+z =2\) |
Exercise 13.7.18 Finding an Equation for a Tangent Plane
Find an equation for the tangent plane to the surface at the given point.
- \( x^{2} +2z^{2} = y^{2} , \: (1,3,-2) \)
Solution Rewrite the equation as
- \( g(x,y,z) = x^{2} -y^{2}+2z^{2} = 0 \)
- \( g_{x}(x,y,z) = 2x \)
- \( g_{y}(x,y,z) = -2y \)
- \( g_{z}(x,y,z) = 4z \)
at \((1,3,-2)\)
- \( g_{x}(1,3,-2) = 2 \)
- \( g_{y}(1,3,-2) = -6 \)
- \( g_{z}(1,3,-2) = -8 \)
| 0 | \(= 2(x-1) + (-6)(y-3)+ (-8)(z+2) \) |
| \(= 2x-2-6y+18-8z-16\) | |
| \(=x-3y-4z \) |
Exercise 13.7.24 Finding an Equation of a Tangent Plane and a Normal Line
Find an equation for the tangent plane and find symmetric equations for the normal line to the surface at the given point.
- \( z = 16-x^{2}-y^{2}, \: (2,2,8)\)
Solution Taking partial derivatives from the given equation produces
- \( f_{x}(x,y) = -2x \)
- \( f_{y}(x,y) = -2y \)
- \( f_{x}(2,2) = -4 \)
- \( f_{y}(2,2) = -4 \)
The equation is
- \( 0 = -4(x-2) -4(y-2) -(z-8) \)
- \( 0 = -4x-4y-z +24 .\)
The parametric equation is
- $$ \frac{x-2}{4} = \frac{y-2}{4} = \frac{z-8}{1}. $$
Exercise 13.7.42 Horizontal Tangent Plane
Find the point(s) on the surface at which the tangent plane is horizontal.
- \( z = 3x^{2} + 2y^{2} -3x + 4y -5 \)
Solution Compute \(z_{x}\) and \(z_{y}\), then solve the system.
| \(z_{x}\) | \(= 6x-3\) |
| \(z_{y}\) | \(= 4y+4 \) |
Which produces the equations
- \(\left\{\begin{matrix} 6x-3 &=0 \\ 4y+4& =0 \end{matrix}\right.,\)
which solves to \(x=1/2\) and \(y=-1\). Plug this into \(z\),
- \(z(1/2,-1) = -43/4 \)
- \( (1/2,-1,-43/4)\)
Internal Links
Parent Article: Calculus III Advanced (Course)