Calculus III Advanced (Course) (13.9) (Homework)

Section 13.9 Homework

From Calculus 10e by Larson and Edwards, p. 949. Exercises 6, 10, 14, 18.

Exercise 13.9.6 Finding Positive Numbers

Find three \(x\), \(y\), and \(z\) positive integers and that satisfy the given conditions. The sum is 32, and \(P=xy^{2}z \) is a maximum.
Solution Let \(x+y+z=32\). Maximize \(P=xy^{2}z \).

\(z\)	\(= 32-x-y\)
\(P(x,y)\)	\(=xy^{2}(32-x-y) \)
\(P_{x}\)	\(= 32y^{2} - 2xy^{2} -y^{3} \)
	\(= y^{2}(32 - 2x -y) = 0 \)
\(P_{y}\)	\(= 64xy - 2x^{2}y -3xy^{} \)
	\(= xy(64 - 2x -3y) = 0 \)

This produces the following critical points.

\((x,0) \text{ for any }x; \: (0,32); \: (8,16).\)

The maximum is obtained when \((x,y)=(8,16)\) for which \(z=32-x-y=8\).

\(P_{max} = 8 \times 16^{2} \times 8 = 16384 \)

Exercise 13.9.10 Maximum Volume

The material for constructing the base of an open box costs 1.5 times as much per unit area as the material for constructing the sides. For a fixed amount of money \(C\) find the dimensions of the box of largest volume that can be made.
Solution Let \(x\), \(y\), and \(z\) be the length, width, and height for the box where \(x>0\) and \(y>0\). The construction cost is \(1.5xy+2(xz+yz)= C\).

\(V\)	\(=xyz \)
\(z\)	$$= \frac{C-1.5xy}{2(x+y)}$$
	Plug \(z\) into \(V\)
\(V(x,y)\)	$$= xy \frac{C-1.5xy}{2(x+y)}$$
	Finding the maximum critical point
\(V_{x}\)	$$ = \frac{(Cy-3xy^{2})(x+y)(Cxy-1.5x^{2}y^{2})}{2(x+y)^{2}} = 0$$
\(V_{y}\)	$$ = \frac{(Cx-3x^{2}y)(x+y)(Cxy-1.5x^{2}y^{2})}{2(x+y)^{2}} = 0$$
\(C\)	\(= 1.5x^{2}+3xy = 1.5y^{2}+3xy\)
	The solutions are
	\(x=y=\sqrt{C/4.5} = \sqrt{2C}/3 \)

The height is

$$ z = \frac{C-1.5xy}{x+y} = \frac{\sqrt{C}}{2\sqrt{2}} .$$

Exercise 13.9.14 Maximum Profit

A corporation manufactures candles at two locations. The cost for producing \(x_{1}\) units at location 1 is

\(C_{1} = 0.02x_{1}^{2} + 4x_{1} + 500 \)

and the cost for producing \(x_{2}\) units at location 2 is

\(C_{2} = 0.05x_{2}^{2} + 4x_{2} + 275. \)

The candles sell for $15 per unit. Find the quantity that should be produced at each location to maximize the profit

\(P=15(x_{1}+x_{2}) -C_{1}-C_{2}.\)

Solution Plug \(C_{1}\) and \(C_{2}\) into the profit equation

\( P=15(x_{1}+x_{2}) - (0.02x_{1}^{2} + 4x_{1} + 500 ) - (0.05x_{2}^{2} + 4x_{2} + 275) \)

\(P_{x_{1}} \)	\(= 15-0.04x_{1}-4 = 0\)
\(P_{x_{2}} \)	\(= 15-0.01x_{2}-4 = 0\)
\((x_{1},x_{2})\)	\(= (275,110) \)

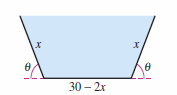
Exercise 13.9.18 Area

Figure 1

A trough with trapezoidal cross sections is formed by turning up the edges of a 30-inch-wide aluminum sheet, as shown in Figure 1. Find the cross section with maximum area. Solution The area equals \(A(x,\theta) \) \(= (30 - 2x + x \cos \theta) \cdot x \sin \theta\) \(= 30x \sin \theta -2 x^{2} \sin \theta + x^{2}\sin \theta \cos \theta. \) Find the maximum by setting: \(A_{x}\) \(=(30+4x+2x \cos \theta) \sin \theta = 0 \) \( \cos \theta = \frac{2x-15}{x}\) \(A_{\theta}\) \(=x(30\cos \theta -2x \cos \theta + x(\cos^{2} \theta-\sin^{2} \theta)) = 0 \) Assume that \(\sin \theta \ne 0\). Substitute \(\cos \theta\) into \(A_{\theta}\) yields \(x\) $$ 30\frac{2x-15}{x} -2x \frac{2x-15}{x}+x \left( \frac{(2x-15)^{2}}{x^{2}}-1 \right) = 0$$ Simplification reduces it to: \( 3x(x-10=0\) Therefore, \(x=10\) and \(\cos \theta = 1/2\). Finally, \(\theta = \frac{\pi}{3} = 60^{\circ} \).

Internal Links

Parent Article: Calculus III Advanced (Course)