Calculus III Advanced (Course) (14.01) (Homework)

Section 14.01 Homework

From Calculus 10e by Larson and Edwards, p. 972. Exercises 28, 32, 42, 56, 60.

Exercise 14.1.28 Evaluate an Iterated Integral

$$ \int_{0}^{\pi/4} \int_{\sqrt{3}}^{\sqrt{3} \cos \theta} r \: dr \: d \theta $$

Solution Take the inner integral and solve

$$ \int_{\sqrt{3}}^{\sqrt{3} \cos \theta} r \: dr $$	$$=\left. \frac{1}{2} r^{2} \right ]_{\sqrt{3}}^{\sqrt{3} \cos \theta}$$
	$$= \frac{1}{2} (\sqrt{3} \cos \theta)^{2} - \frac{1}{2} (\sqrt{3})^{2} $$
	$$= \frac{1}{2} (3 \cos^{2} \theta) - \frac{1}{2} 3$$
	$$= \frac{3}{2} \cos^{2} \theta - \frac{3}{2}$$

Take the outer integral and solve.

$$\int_{0}^{\pi/4} \frac{3}{2} \cos^{2} \theta - \frac{3}{2} \: d \theta$$	$$= \frac{3}{2} \int_{0}^{\pi/4}( \cos^{2} \theta - 1) \: d \theta$$
	$$= \frac{3}{2} \int_{0}^{\pi/4}(- \sin^{2} \theta) \: d \theta \:\:\:\: \color{red}{ \text{Trigonometric Identity}}$$
	$$= -\frac{3}{2} \int_{0}^{\pi/4}\sin^{2} \theta \: d \theta\:\:\:\: \color{red}{ \text{Carry the minus sign out}}$$
	$$= -\frac{3}{2} \int_{0}^{\pi/4} \frac{1- \cos(2 \theta)}{2} \: d \theta \:\:\:\: \color{red}{ \text{Half angle}}$$
	$$ =\left.- \frac{3}{4} \left( \theta - \frac{\sin (2 \theta)}{2} \right) \right]_{0}^{\pi/4} \:\:\:\: \color{red}{ \text{Carry 1/2 out and integrate}} $$
	$$= - \frac{3}{4} \left( \frac{\pi}{4} - \frac{1}{2} \right) = \frac{3}{8} - \frac{3 \pi}{16} $$

Exercise 14.1.32 Evaluating an Improper Iterated Integral

Evaluate the improper iterated integral.

$$ \int_{0}^{3} \int_{0}^{ \infty } \frac{x^{2}}{1+y^{2}} dy \: dx $$

Solution Start with the inner integral.

$$ \int_{0}^{ \infty } \frac{x^{2}}{1+y^{2}} dy $$	$$= x^{2}\int_{0}^{ \infty } \frac{1}{1+y^{2}} dy$$
	$$= \left. \vphantom{\frac{1}{2}} x^{2} \arctan y \right]_{0}^{ \infty } \:\:\:\: $$	Trigonometric Identity
	\(= x^{2} \arctan \infty - x^{2} \arctan 0 \)
	$$= x^{2} \frac{\pi}{2} $$

Now for the outer integral

$$ \int_{0}^{3} x^{2} \frac{\pi}{2} \: dx$$	$$= \frac{\pi}{2}\left[ \frac{ x^{3}}{3} \right]_{0}^{3} $$
	$$= \frac{\pi}{2}\left[ \frac{(3)^{3}}{3} - \frac{(0)^{3}}{3} \right] = \frac{9 \pi}{2}$$

Exercise 14.1.42 Find the Area for a Region

Use an iterated integral to find the area for the region bounded by the graphs for the equations

$$ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 $$

Solution Let the bounds for \(x = -a,a\). Solving the bounds for \(y\) produces:

$$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} $$	$$= 1$$
$$ \frac{y^{2}}{b^{2}} $$	$$=1- \frac{x^{2}}{a^{2}} $$
$$ \frac{y}{b} $$	$$= \sqrt{1- \frac{x^{2}}{a^{2}}} $$
\(y\)	$$=b \sqrt{1- \frac{x^{2}}{a^{2}}} $$	Bounds for \(y\).

This produces a formula for the area. $$ \int \int_{R} dA = \int_{-a}^{a} \int_{-b \sqrt{1-x^{2}/a^{2}}}^{b \sqrt{1-x^{2}/a^{2}}}\:dy \:dx \:\:\:\: \text{ Using }dy \:dx \text{ order.}$$

$$ \int_{-a}^{a} \int_{-b \sqrt{1-x^{2}/a^{2}}}^{b \sqrt{1-x^{2}/a^{2}}}\:dy \:dx $$	$$= \left. \int_{-a}^{a} y \right]_{-b \sqrt{1-x^{2}/a^{2}}}^{b \sqrt{1-x^{2}/a^{2}}} \:dx $$	Integrate with respect to \(y\)
	$$= \int_{-a}^{a} b \sqrt{1 - \frac{x^{2}}{a^{2}}} - \left( - b \sqrt{1 - \frac{x^{2}}{a^{2}}} \right) \:dx $$
	$$= \int_{-a}^{a} 2b \sqrt{1 - \frac{x^{2}}{a^{2}}} \:dx = 2b \int_{-a}^{a} \sqrt{1 - \frac{x^{2}}{a^{2}}} \:dx$$	Move the constant out.
	$$x= \frac{1}{1/a} \sin u$$	Apply Trig substitution
	$$= 2ba \int_{-a}^{a} \cos u \sqrt{ 1-\sin^{2} u } \: du $$
	$$= 2ba \int_{-a}^{a} \cos u \sqrt{ \cos^{2} u } \: du $$	Trig Identity
	$$= 2ba \int_{-a}^{a} \cos u \cos u \: du $$	Trig Identity
	$$= 2ba \int_{-a}^{a} \cos^{2} u \: du $$	Trig Identity
	$$= 2ba \int_{-a}^{a} \frac{1+\cos(2u)}{2} \: du $$	Trig Identity
	$$= ba \int_{-a}^{a} 1 \: du + \cos(2u)\: du $$	Pull out the 1/2 and apply the Sum Rule.
	$$= ba \int_{-a}^{a} u + \frac{1}{2} \sin (2u) $$	Trig Identity
	$$ u= \arcsin (\frac{1}{a})x $$	Back substitution
	$$= ba \int_{-a}^{a} u + \frac{1}{2} \sin (2u) $$
	$$= ba \int_{-a}^{a}\left( \arcsin \frac{x}{a} + \frac{1}{2} \sin \left( 2 \arcsin \frac{x}{a} \right) \right) \:dx $$
	$$= \frac{\pi}{2}ba- \left( -\frac{\pi}{2}ba \right) = \pi ba $$

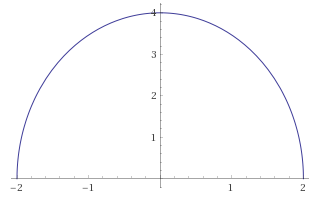
Exercise 14.1.56 Switching the Integration Order

Sketch the region \(R\) whose area is given by the iterated integral. Then switch the integration order and show that both orders yield the same area.

$$ \int_{-2}^{2} \int_{-\sqrt{4-x^{2}}}^{\sqrt{4-x^{2}}} dy \:dx $$

Solution

$$ \left. \int_{-2}^{2} y \right]_{-\sqrt{4-x^{2}}}^{\sqrt{4-x^{2}}} \:dx $$	$$=\int_{-2}^{2} (\sqrt{4-x^{2}} - (-\sqrt{4-x^{2}})) \: dx$$
	$$= \int_{-2}^{2} 2\sqrt{4-x^{2}} \: dx$$
	$$= 2 \int_{-2}^{2} \sqrt{4-x^{2}} \: dx$$
	\( x=2 \sin u \)	Trig Substitution
	$$= 4 \int \cos u \sqrt{- \sin^{2} u + 1} \: du $$
	$$= 4 \int \cos u \sqrt{ \cos^{2} u } \: du $$
	$$= 4 \int \cos^{2} u \: du $$
	$$= 4 \int \frac{1+ \cos 2u}{2} \: du $$	Trig Identity
	$$= 2 \int 1 \: du+ \int \cos 2u \: du $$	Trig Identity
	$$= 2 ( u+ \frac{1}{2} \sin 2u ) $$	Trig Identity
	$$u= \arcsin \frac{1}{2}x$$	Back substitute
	$$= 2 \arcsin \frac{1}{2}x + \sin \left( 2 \arcsin \frac{1}{2}x \right)$$
	\(= 2 * 2\pi = 4 \pi\)

Figure 1

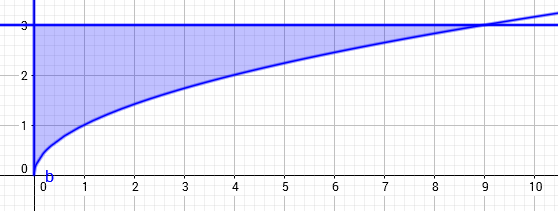
Exercise 14.1.60 Switching the Integration Order

Sketch the region \(R\) whose area is given by the iterated integral. Then switch the integration order and show that both orders yield the same area.

$$ \int_{0}^{9} \int_{\sqrt{x}}^{3} dy \: dx$$

Solution The region is \(0 \leqslant x \leqslant 9 \) and \( \sqrt{x} \leqslant y \leqslant 3\).

$$ \int_{0}^{9} \int_{\sqrt{x}}^{3} dy \: dx $$	$$= \left. \int_{0}^{9} y \right]_{\sqrt{x}}^{3} \: dx $$
	$$= \int_{0}^{9} (3-\sqrt{x}) \: dx $$
	$$= \left. 3x- \frac{2}{3} x^{3/2} \right]_{0}^{9} = 27-18 = 9$$

Now reverse the integration order.
To match the bounds set 0 to \(y^{2} = 9\).

$$ \int_{0}^{3} \int_{0}^{y^{2}} dx \: dy $$	$$= \left. \int_{0}^{3} x \right]_{0}^{y^{2}} \: dy $$
	$$= \int_{0}^{3} y^{2}\: dy $$
	$$= \left. \frac{1}{3} y^{3} \right]_{0}^{3} = \frac{1}{3} 3^{3} = 9$$

Figure 2

Internal Links

Parent Article: Calculus III Advanced (Course)