Calculus III Advanced (Course) (14.04) (Homework)

Section 14.4 Homework

From Calculus 10e by Larson and Edwards, p. 1000. Exercises 8,33

Exercise 14.4.8 Finding the Mass Center

Figure 1

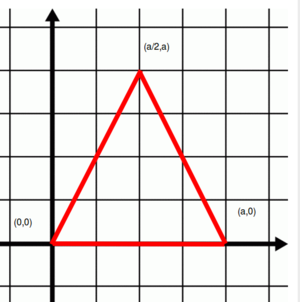
Find the mass and mass center for the lamina at each density. \(R\): triangle with vertices \((0,0),\:(a/2,a),\:(a,0)\) (a) \(\rho=k\) (b) \(\rho=kxy\) Solution The triangle is equilateral, as shown in Figure 1. From geometry the triangle has the area \(\frac{a^{2}}{2}\). The bounds are \(x=y/2, \: x=a-y/2\) and \(y=a\).

(a). The density at any point \((x,y)\) is \(k\) since \(\rho=k\).

$$m$$	$$=\int_{R} \int k \: dA $$
	$$= \int_{0}^{a} \int_{y/2}^{a-y/2} k \:dx \: dy $$
	$$= k \left. \int_{0}^{a} x \right]_{y/2}^{a-y/2} \: dy$$
	$$= k \int_{0}^{a} a-y \: dy$$
	$$= k \left[ a-\frac{1}{2}y^{2} \right]_{0}^{a} $$
	$$= k \left[ a - \frac{1}{2} a^{2}- a \right] = \frac{a^{2}}{2} k $$	mass for the lamina

Find the moment about the \(x\)-axis. The bounds for \(x\) are \(0 \leqslant x \leqslant a/2\).

$$M_{x} $$	$$= \int_{0}^{a/2} \int_{0}^{a} (y)(k) \: dy \: dx $$
	$$= k \int_{0}^{a/2} \left. \frac{1}{2} y^{2} \right]_{0}^{a} \: dx $$
	$$= \frac{1}{2} a^{2}(k) \int_{0}^{a/2} \: dx $$
	$$= \left. \frac{1}{2} a^{2}(k)\:\: x \right]_{0}^{a/2} $$
	$$= \frac{a^{2}}{2} \times \frac{a}{2} \times k = \frac{a^{3}}{4}k$$

This produces $$\bar{y} = \frac{M_{x}}{m}=\frac{ \frac{a^{3}}{4}k }{ \frac{a^{2}}{2}k} = \frac{a}{2}$$

The mass center is

$$ \left( \frac{a}{2}, \frac{a}{2} \right). $$

(b). The density at any point \((x,y)\) is \(kxy\) since \(\rho=kxy\).

$$m$$	$$=\int_{R} \int kxy \: dA $$
	$$= \int_{0}^{a} \int_{y/2}^{a-y/2} kxy \:dx \: dy $$
	$$= k \left. \int_{0}^{a} x^{2}y \right]_{y/2}^{a-y/2} \: dy$$
	$$= k \int_{0}^{a} y(a-\frac{y}{2})^{2} - \frac{y^{3}}{4} \: dy$$
	$$= ak \int_{0}^{a} (ay-y^{2}) \: dy $$
	$$= ak \left[ \frac{1}{2}(a)y^{2} - \frac{1}{3}y^{3} \right]_{0}^{a} $$
	$$= ak \left[ \frac{a^{3}}{2} - \frac{a^{3}}{3} \right] $$
	$$= ak \left[ \frac{3a^{3}}{6} - \frac{2a^{3}}{6} \right] $$
	$$= ak \left[ \frac{a^{3}}{6} \right] = \frac{ka^{4}}{6}$$	mass for the lamina

Find the moment about the \(x\)-axis. The bounds for \(x\) are \(0 \leqslant x \leqslant a/2\).

$$M_{x} $$	$$= \int_{0}^{a/2} \int_{0}^{a} (y)(kxy) \: dy \: dx $$
	$$= k \int_{0}^{a/2} \left. \frac{1}{3} y^{3}x \right]_{0}^{a} \: dx $$
	$$= \frac{1}{3} a^{3}(k) \int_{0}^{a/2} \: dx $$
	$$= \frac{1}{3} a^{3}(k) \left[ \vphantom{\frac{1}{2}} x \right]_{0}^{a/2} $$
	$$= \frac{1}{3} a^{3}(k) \left( \frac{a}{2} \right) = \frac{ka^{4}}{6}$$

This produces $$\bar{y} = \frac{M_{x}}{m}=\frac{\frac{ka^{4}}{6} }{ \frac{ka^{4}}{6}} = 1$$

The mass center is

$$ \left( \frac{a}{2}, 1 \right). $$

Exercise 14.4.33 Finding Inertia Moments and Gyration Radii

Figure 2

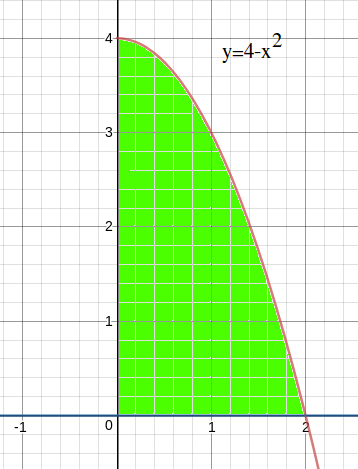
Find \(I_{x}, \: I_{y}, \: I_{0}, \: \bar{\bar{x}} \text{, and } \bar{\bar{y}} \) for the lamina bounded by the graphs, \(y = 4-x^{2} \) \( y=0\) \( x > 0\) \( \rho = kx,\) as shown in Figure 2.

Solution The bounds are:

\( 0 \leqslant x \leqslant 2\),

\( 0 \leqslant y \leqslant 4-x^{2} \).

and

\( y=0 \).

Inertia Moment about the \(x\)-axis.

$$I_{x} $$	$$= \int_{0}^{2} \int_{0}^{4-x^{2}} y^{2}(kx) \: dy \: dx $$
	$$=k \int_{0}^{2} \left. \frac{1}{3}y^{3} x \right]_{0}^{4-x^{2}} \: dx $$
	$$= \frac{1}{3} k \int_{0}^{2} x(4-x^{2})^{3} \: dx $$
	$$= \frac{1}{3} k \int_{0}^{2} x(-x^{6}+12x^{4}-48x^{2}+64) \: dx = \frac{32}{3}k $$

Inertia Moment about the \(y\)-axis.

$$I_{y} $$	$$= \int_{0}^{2} \int_{0}^{4-x^{2}} x^{2}(kx) \: dy \: dx $$
	$$=k \left. \int_{0}^{2} x^{3}y \right]_{0}^{4-x^{2}} \: dx $$
	$$= k \int_{0}^{2} x^{3}(4-x^{2}) \: dx $$
	$$= k \left[ x^{4}- \frac{1}{6} x^{6} \right]_{0}^{2} = \frac{16}{3}k $$

Polar Inertia Moment \(I_{0}\).

$$ \frac{32}{3}k + \frac{16}{3}k = 16k$$

Gyration Radius about the \(y\)-axis.

$$\bar{ \bar{x}} $$	$$= \sqrt{\frac{I_{y}}{m}} $$
	$$= \sqrt{\frac{\frac{16}{3}k}{4k}} = \frac{2\sqrt{3}}{3}$$

Gyration Radius about the \(x\)-axis.

$$\bar{ \bar{y}} $$	$$= \sqrt{\frac{I_{x}}{m}} $$
	$$= \sqrt{\frac{\frac{32}{3}k}{4k}} = \frac{2\sqrt{6}}{3}$$

Internal Links

Parent Article: Calculus III Advanced (Course)