Calculus III Advanced (Course) (15.01) (Homework)

Section 15.1 Homework

From Calculus 10e by Larson and Edwards, p. 1049. Exercises 1, 2, 3, 4, 8, 34, 40, 44, 60.

Exercises 1-4 Matching

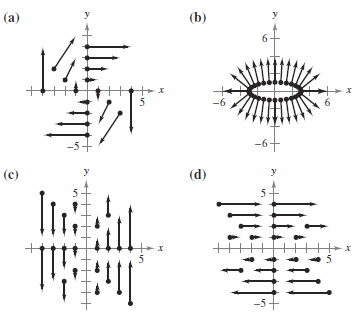
Match the vector field with its graph in Figure 1.

Figure 1

Exercise 15.1.1 Matching

\(\textbf{F}(x,y)=y\textbf{i}\)

Solution d

Exercise 15.1.2 Matching

\(\textbf{F}(x,y)=x\textbf{j}\)

Solution c

Exercise 15.1.3 Matching

\(\textbf{F}(x,y)=y\textbf{i} - x\textbf{j}\)

Solution a

Exercise 15.1.4 Matching

\(\textbf{F}(x,y)=x\textbf{i} + 3y\textbf{j} \)

Solution b

Exercise 15.1.8 Sketching a Vector Field

Find \( \| \textbf{F} \| \) and sketch several representative vectors in the vector field.

\( \textbf{F}(x,y) = y\textbf{i}+x\textbf{j}\)

Solution

Figure 2

Exercise 15.1.34 Finding a Potential Function

Determine if the vector field is conservative. If so, find a potential function for the vector field.

\(\textbf{F}(x,y) = 3x^{2}y^{2}\textbf{i}+2x^{3}y\textbf{j}\)

Solution Applying Theorem 15.1.1 yields that \(\textbf{F}\) is not conservative because

$$ \frac{\partial}{\partial y}[3x^{2}y^{2}] = 3x^{2}2y \text{ and }\frac{\partial}{\partial x}[2x^{3}y]=6x^{2}y$$

Exercise 15.1.40 Finding a Potential Function

Determine if the vector field is conservative. If so, find a potential function for the vector field.

$$\textbf{F}(x,y) = \frac{x\textbf{i}+y\textbf{j}}{x^{2}+y^{2}}$$

Solution The vector field \(\textbf{F}\) is not conservative because

$$\frac{\partial}{\partial x}=\frac{-x^{2}-2xy+y^{2}}{(x^{2}+y^{2})^{2}} \text{ and }\frac{\partial}{\partial y}=\frac{-y^{2}-2x+y^{2}}{(x^{2}+y^{2})^{2}} $$

Exercise 15.1.44 Finding the Curl of a Vector Field

Find curl F for the vector field at the given point.

\(\textbf{F}(x,y,z) = x^{2}z\textbf{i}-2xz\textbf{j}+yz\textbf{k}; \: (2,-1,3)\)

Solution

curl \( \{x^{2}z,-2xz,yz\}\)	\(= (2x+z,x^{2},-2z)\)
	\(= (2(2)+3)\textbf{i}-2^{2} \textbf{j}+(-1)(3) \textbf{k}\)
	\(=7-4-3=0 \)

Exercise 15.1.60 Finding the Divergence of a Vector Field

Find the divergence for the vector field \(\textbf{F}\).

\(\textbf{F}(x,y,z)=\ln(x^{2}+y^{2})\textbf{i}+xy\textbf{j}+\ln(y^{2}+z^{2})\textbf{k}\)

Solution

$$\text{div}\ln(x^{2}+y^{2})\textbf{i}+xy\textbf{j}+\ln(y^{2}+z^{2})\textbf{k}= \frac{2x}{x^{2}+y^{2}}+x+\frac{2z}{y^{2}+z^{2}} $$

Internal Links

Parent Article: Calculus III Advanced (Course)