Calculus II 07.04 Arc Length and Surfaces for Revolution

Previous	Calculus II 07.03 Volume The Shell Method
Next	Calculus II 07.05 Work

7.4 Arc Length and Surfaces for Revolution

• Find the arc length for a smooth curve.
• Find the area for a rotate surface.

Arc Length

Figure 7.4.1

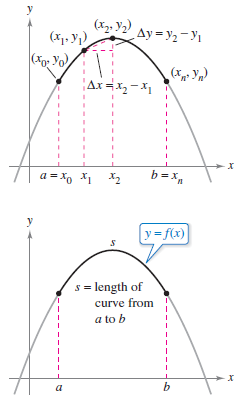
Arc lengths are found by using integrals and the areas for rotated surfaces. In either case, an arc (a segment of a curve) is approximated by straight line segments whose lengths are given by the familiar Distance Formula $$d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}.$$ A rectifiable curve is one that has a finite arc length. The function \(f\)'s graph is rectifiable between \((a,f(a))\) and \(b,f(b))\) and that \(f^{\prime }\) be continuous on \([ a,b ] \). Such a function is continuously differentiable on \([ a,b ] \), and its graph on the interval \([ a,b ] \) is a smooth curve. Consider a function \(y=f(x)\) that is continuously differentiable on the interval \([ a,b ] \). You can approximate \(f\)'s graph by \(n\) line segments whose endpoints are determined by the partition $$a=x_{0}<x_{1}<x_{2}\cdots<x_{n}=b $$ as shown in Figure 7.37. By letting \(\Delta x_{i}=x_{i}-x_{i-1}\) and \(\Delta y_{i}=y_{i}-y_{i-1}\), you can approximate the graph's length by $$S$$ $$ \approx \sum_{i=1}^{n} \sqrt{(x_{i}-x_{i-1})^{2}+(y_{i}-y_{i-1})^{2}} $$ $$ = \sum_{i=1}^{n} \sqrt{(\Delta x_{i})^{2}+(\Delta y_{i})^{2}} $$ $$ = \sum_{i=1}^{n} \sqrt{ (\Delta x_{i})^{2}+ \left( \frac{ \Delta y_{i}}{ \Delta x_{i} } \right)^{2} (\Delta x_{i})^{2} } $$ $$ = \sum_{i=1}^{n} \sqrt{ 1 + \left( \frac{ \Delta y_{i}}{ \Delta x_{i} } \right)^{2}} (\Delta x_{i}) $$ This approximation improves as \(\left \| \Delta \right \|\rightarrow 0(n\rightarrow \infty )\). The graph's length is $$ S = \lim_{ \left \| \Delta \right \|\rightarrow 0} \sum_{i=1}^{n} \sqrt{ (\Delta x_{i})^{2}+ ( \frac{ \Delta y_{i}}{ \Delta x_{i} } )^{2}} (\Delta x_{i}) $$ Because \(f^{\prime }(x)\) exists for each \(x\) in \((x_{i-1},x_{i})\), the Mean Value Theorem guarantees that \(c_{i}\) exists in \((x_{i-1},x_{i})\) such that $$ f(x_{i})-f(x_{i-1}) $$ $$ = f^{\prime }(c_{i})(x_{i}-x_{i-1})$$ $$ \frac{f(x_{i})-f(x_{i-1})}{x_{i}-x_{i-1}} $$ $$ = f^{\prime }(c_{i})$$ $$ \frac{\Delta y_{i} }{\Delta x_{i}} $$ $$ = f^{\prime }(c_{i}). $$ Because \( f^{\prime }\) is continuous on \([ a,b ] \), if follows that \( \sqrt{1+ [f^{\prime }(x) ]^{2} } \) is also continuous (and therefore integrable) on \([ a,b ] \), which implies that $$s$$ $$ = \lim_{ \left \| \Delta \right \|\rightarrow 0} \sum_{i=1}^{n} \sqrt{ 1 + \left[ f^{\prime }(c_{i}) \right]^{2}} (\Delta x_{i}) $$ $$ = \int_{a}^{b} \sqrt{ 1 + [ f^{\prime }(x)]^{2}} \: dx $$ where \(s\) is called the arc length for \(f\) between \(a\) and \(b\).

Definition 7.4.1 Arc Length

Let the function \(y=f(x)\) represent a smooth curve on the interval \([ a,b ] \). The arc length for the graph \(f\) between \(a\) and \(b\).

$$S = \int_{a}^{b} \sqrt{ 1 + [ f^{\prime }(x)]^{2}} \: dx .$$

Similarly, for a smooth curve \(x=g(y)\), the arc length for the graph \(g\) between \(c\) and \(d\) is

$$ S = \int_{c}^{d} \sqrt{ 1 + \left[ g^{\prime }(y) \right]^{2}} \: dy .$$

• To see how arc length can be used to define trigonometric functions, see the article “Trigonometry Requires Calculus, Not Vice

Versa” by Yves Nievergelt in UMAP Modules.

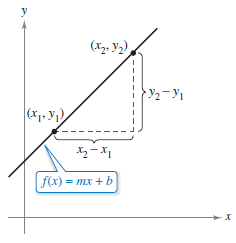
Example 7.4.1 Line Segment Length

The arch length from \((x_{1},y_{1})\) to \((x_{2},y_{2})\) is the standard Distance Formula. Figure 7.4.2

Find the arc length from \((x_{1},y_{1})\) to \((x_{2},y_{2})\) on the graph $$f(x)=mx+b $$ as shown in Figure 7.4.2 Solution Because $$m=f^{\prime }(x)=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$ it follows that $$s$$ $$ = \int_{x_{1}}^{x_{2}} \sqrt{ 1 + \left[ f^{\prime }(x) \right] ^{2}} \:dx $$ Formula for arc length $$ = \int_{x_{1}}^{x_{2}} \sqrt{ 1 + \left( \frac{y_{2}-y_{1}}{x_{2}-x_{1}} \right)^{2}} \:dx $$ $$ = \sqrt{ \frac{ (x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2} }{ (x_{2}-x_{1})^{2} }} (x) \Bigg]_{x_{1}}^{x_{2}} $$ Integrate and simplify $$ = \sqrt{ \frac{ (x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2} }{ (x_{2}-x_{1})^{2} }} (x_{2}-x_{1}) $$ $$ = \sqrt{ (x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2} } $$ which is the formula for the distance between two points in the plane.

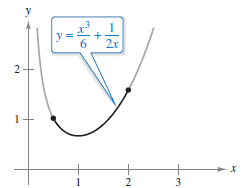
Example 7.4.2 Finding a Bowed Arc Length

The arc length for \(y\)'s graph over \([1/2,2]\). Figure 7.4.3

Find the arch length for the graph $$y= \frac{x^{3}}{6}+\frac{1}{2x}$$ on the interval \([ \frac{1}{2}, 2 ] \), as shown in Figure 7.4.3 Solution Using $$ \frac{dy}{dx} = \frac{3x^{2}}{6} - \frac{1}{2x^{2}} = \frac{1}{2} \left(x^{2}- \frac{1}{x^{2}} \right) $$ yields the arc length formula $$ S$$ $$ = \int_{a}^{b} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \: dx $$ Formula for arc length $$ = \int_{\frac{1}{2}}^{2} \sqrt{1 + \left[ \frac{1}{2} \left( x^{2} - \frac{1}{x^{2}} \right) \right]^{2}} \: dx $$ $$ = \int_{\frac{1}{2}}^{2} \sqrt{ \frac{1}{4} + \left( x^{4} + 2 + \frac{1}{x^{4}} \right)} \: dx $$ Substitute in the equation $$= \int_{\frac{1}{2}}^{2} \frac{1}{2}( x^{2} + \frac{1}{x^{2}}) \: dx $$ Simplify $$= \frac{1}{2} \left[ \frac{x^{3}}{3} - \frac{1}{x} \right]_{\frac{1}{2}}^{2} $$ Integrate $$= \frac{1}{2} \left( \frac{13}{6} + \frac{47}{24} \right) = \frac{33}{16}.$$

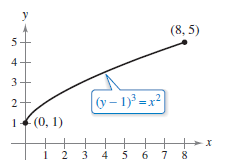
Example 7.4.3 Finding Arc Length

The arc length for \(y\)'s graph over \([0,8]\). Figure 7.4.4

Find the arc length for the graph, \( (y-1)^{3}=x^{2} \) over the interval \( [ 0,8 ] \), as shown in Figure 7.4.4. Solution Begin by solving for \(x\) in terms of \(y: \: x= \pm (y-1)^{\frac{3}{2}} \). Choosing positive values for \(x\) produces $$\frac{dx}{dy}=\frac{3}{2}(y-1)^{\frac{1}{2}} .$$ The \(x\)-interval \( [ 0,8 ] \) corresponds to the \(y\)-interval \( [ 1,5 ] \), and the arc length is $$ s $$ $$= \int_{c}^{d} \sqrt{1 + \left( \frac{dx}{dy} \right)^{2}} \: dy $$ Formula for arc length $$= \int_{1}^{5} \sqrt{1 + \left[ \frac{3}{2}(y-1)^{\frac{1}{2}} \right]^{2} } \: dy \:\:\:\: $$ Substitute in the equation $$= \int_{1}^{5} \sqrt{\frac{9}{4}y-\frac{5}{4} } \: dy $$ Simplify $$= \frac{1}{2} \int_{1}^{5} \sqrt{ 9y-5 } \: dy $$ Integrate $$= \frac{1}{18} \left[ \frac{(9y-5)^{\frac{3}{2}}}{ 3/2 } \right]_{1}^{5} $$ $$ = \frac{1}{27} \left( 40^{3/2}-4^{3/2} \right) \approx 9.073$$

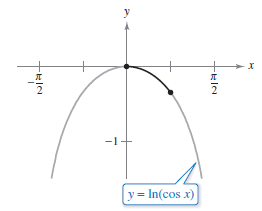
Example 7.4.4 Finding Arc Length

The arc length for \(y\)'s graph over \([0,\pi /4]\). Figure 7.4.5

Find the arc length for the graph< $$y=\ln (\cos x) $$ from \(x=0\) to \(x=\pi / 4 \), as shown in Figure 7.4.5 Solution Using $$\frac{dy}{dx}= - \frac{\sin x}{\cos x}=-\tan x $$ yields the arc length $$ s $$ $$= \int_{a}^{b} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \: dx $$ Formula for arc length $$ = \int_{0}^{\pi /4} \sqrt{1 + \tan^{2}x } \: dx $$ $$ = \int_{0}^{\pi /4} \sqrt{ \sec^{2}x } \: dx $$ Trigonometric identity $$ = \int_{0}^{\pi /4} \sec x \: dx $$ Simplify $$ = \Large\left[ \ln | \sec\:x + \tan x | \Large\right]_{0}^{\pi /4} $$ Integrate \( = \ln ( \sqrt{2} + 1 ) - \ln 1 \approx 0.881 \)

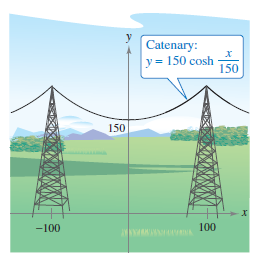
Example 7.4.5 Cable Length with Sag

Figure 7.4.6

An electric cable is hung between two towers that are 200 feet apart, as shown in Figure 7.4.6. The cable takes a catenary shape whose equation is $$y=75 \left( e^{x/150} + e^{-x/150} \right) = 150 \cosh \frac{x}{150} .$$ Find the arc length for the cable between the two towers. Solution Because \(y^{\prime }= \frac{1}{2} \left( e^{x/150} + e^{-x/150} \right)\), $$ \left( y^{\prime } \right)^{2}= \frac{1}{4} \left( e^{x/75} - 2 + e^{-x/75} \right) $$ and $$1 + \left( y^{\prime } \right)^{2} = \frac{1}{4} \left( e^{x/75} + 2 + e^{-x/75} \right) = \left[ \frac{1}{2} \left( e^{x/150} + e^{-x/150} \right) \right]^{2}.$$ This yields the cable's arc length $$ S$$ $$ = \int_{a}^{b} \sqrt{1 + \left( y^{\prime } \right)^{2}} \: dx $$ Formula for arc length $$ = \frac{1}{2} \int_{-100}^{100} \left( e^{x/150} + e^{-x/150} \right) \: dx $$ Substitute $$ = 75 \left[ e^{x/150} - e^{-x/150} \right]_{-100}^{100} $$ Integrate $$ = 150 \left( e^{x/150} - e^{-x/150} \right) \approx 215 \: feet.$$

Area for a Rotated Surface

In Sections 7.2 and 7.3 , integration was used to calculate the volume for a rotated solid. Here integration is used to find the area for a rotated surface.

Definition 7.4.2 A Rotated Surface

Figure 7.4.7 Figure 7.4.8 Figure 7.4.9

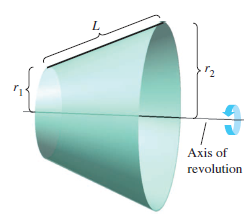
When the graph for a continuous function is revolved about a line, the resulting surface is a rotated surface. The area for a rotated surface is calculated using the formula for a right circular cone's frustum area. Consider the line segment in Figure 7.4.7, where \(L\) is the line segment length, \(r_{1}\) is the radius at the left end, and \(r_{2}\) is the radius at the right end. 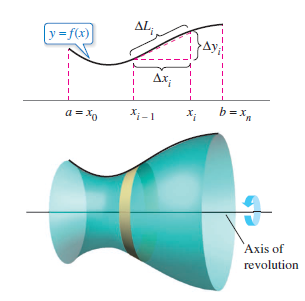When the line segment is rotated about the axis, it forms a frustum for a right circular cone, with \( S = 2 \pi rL \) Frustum's lateral surface area where $$r = \frac{1}{2} \left( r_{1}+r_{2} \right) \:\:\:\: \color{red}{\text{ Frustrum's average radius }} $$ Consider a function \(f\) that has a continuous derivative on the interval \([ a,b ] \). The graph for \(f\) is rotated about the \(x\)-axis to form the surface shown in Figure 7.4.8. Let \(\Delta \) be a partition over \([ a,b ]\) with subintervals \(\Delta x_{i} \) wide. Then the line $$ \Delta L_{i} = \sqrt{ \Delta x_{i}^{2} + \Delta y_{i}^{2} } $$ generates a frustum. Let \(r_{i}\) be the average radius. By the Intermediate Value Theorem[1], a point \(d_{i}\) exists (in the \(i\)th subinterval) such that \(r_{i} = f(d_{i}) \). The lateral surface area \(\Delta S_{i}\) for the frustum is \(\Delta S_{i}\) \(= 2\pi r_{i}\Delta L_{i} \) $$= 2\pi f(d_{i}) \sqrt{ \Delta x_{i}^{2} + \Delta y_{i}^{2} } $$ $$= 2\pi f \left( d_{i} \right) \sqrt{ 1 + \left( \frac{\Delta y_{i} }{\Delta x_{i}} \right)^{2} } \Delta x_{i} .$$ By The Mean Value Theorem [2], a point \(r_{i} \) exists in \(x_{i-1},x_{i}) \) that \(f^{\prime }(c_{i}) \) $$ = \frac{f(x_{i}) - f(x_{i-1})}{ x_{i}-x_{i-1}} $$ $$ = \frac{\Delta y_{i}}{\Delta x_{i}} .$$ Therefore, \( \Delta S_{i} = 2 \pi f(d_{i}) \sqrt{1+[f^{\prime }(c_{i})]^{2} }\Delta x_{i} \), and the total surface area can be approximated by $$\Delta S_{i} \approx 2 \pi \sum_{i-1}^{n} f(d_{i}) \sqrt{1+[f^{\prime }(c_{i})]^{2} }\Delta x_{i} .$$ The limit as \( \| \Delta \|\rightarrow 0(n \to \infty ) \) is $$ S = 2 \pi \int_{a}^{b} f(x) \sqrt{1+ \left[ f^{\prime }(x) \right]^{2} } dx .$$ 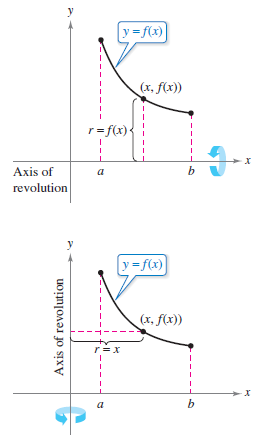The vertical formula for \(S\), the graph is rotated about the \(y\)-axis, has \(2\pi x\) for the circumference and \(r=x\) for the radius. The horizontal formula for \(S\), the graph is rotated about the \(x\)-axis, has \(2\pi f(x)\) for the circumference and \(r=f(x)\) for the radius. See Figure 7.4.9. By appropriately adjusting \(r\), you can generalize the formula to cover any horizontal or vertical axis as indicated in the next definition.

Definition 7.4.3 Rotated Surface Area

Let \(y=f(x)\) have a continuous derivative over the interval \([a,b]\). Rotating \(f\)'s graph about a horizontal or vertical axis produces an area \(S\) with the formula

$$ S = 2 \pi \int_{a}^{b} r(x) \sqrt{1+ \left[ f^{\prime }(x) \right]^{2} } dx \:\:\:\: \color{red}{y \text{ is a function for }x} $$

where \(r\) is the distance between \(f\)'s graph and the axis. If \(x=g(y)\) on the interval \([c,d]\), then the surface area is

$$ S = 2 \pi \int_{c}^{d} r(y) \sqrt{1+ \left[ g^{\prime }(y) \right]^{2} } dy \:\:\:\: \color{red}{ x \text{ is a function for }y}$$

where \(r(y)\) is the distance between \(g\)'s graph and the axis. The formulas in this definition are sometimes written as

$$ S = 2 \pi \int_{a}^{b} r(x)\:ds \:\:\:\: \color{red}{ y \text{ is a function for }x}$$

and

$$S = 2 \pi \int_{c}^{d} r(y)\:ds \:\:\:\: \color{red}{x \text{ is a function for }y}$$

where

$$ds=\sqrt{1+ \left[ f^{\prime }(x) \right]^{2} } dx \text{ and }ds=\sqrt{1+ \left[ g^{\prime }(y) \right]^{2} } dy,$$

respectively.

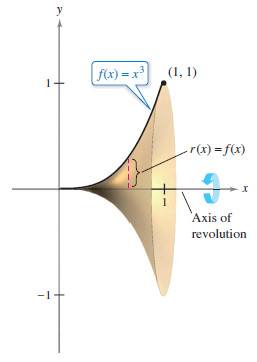
Example 7.4.6 The Area for a Horizontal Rotated Surface

Figure 7.4.10

Find the area for the rotated surface formed by rotating the graph \(f(x)=x^{3}\) over the interval \([0,1]\) about the \(x\)-axis, as shown in Figure 7.4.10. Solution The distance between the \(x\)-axis and the graph for \(f\) is \(r(x)=f(x)\), and because \( f^{\prime }(x)=3x^{2} \), the surface area is $$ S $$ $$ = 2 \pi \int_{a}^{b} r(x) \sqrt{1+ \left[ f^{\prime }(x) \right]^{2} } dx $$ Formula for surface area $$ = 2 \pi \int_{0}^{1} x^{3} \sqrt{1+ \left( 3x^{2} \right)^{2} } dx $$ Add functions $$ = \frac{ 2 \pi}{36} \int_{0}^{1} \left( 36x^{3} \right) \left( 1+9x^{4} \right)^{1/2} dx $$ Simplify $$ = \frac{\pi}{18} \left[ \frac{ \left( 1+9x^{4} \right)^{3/2}}{3/2} \right]_{0}^{1} $$ Integrate $$ = \frac{ \pi}{27} \left( 10^{3/2}-1 \right)\approx 3.563 $$

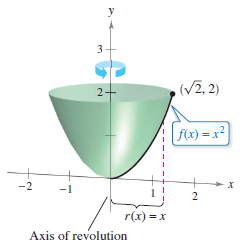
Example 7.4.7 The Area for a Vertical Rotated Surface

Figure 7.4.11

Find the area formed by rotating the graph \(f(x)=x^{2}\) over the interval \([0,\sqrt{2}]\) about the \(y\)-axis, as shown in Figure 7.4.11. Solution The distance between the graph and the \(y\)-axis is \(r(x)=x\). Using \(f^{\prime }(x)=2x\) and the surface area formula produces $$ S $$ $$ = 2 \pi \int_{a}^{b} r(x) \sqrt{1+ \left[ f^{\prime }(x) \right]^{2} } dx \:\:\:\: $$ Formula for surface area $$ = 2 \pi \int_{0}^{1} x \sqrt{1+(2x)^{2} } dx $$ $$ = 2 \pi \int_{0}^{\sqrt{2}} \left( 1+4x^{2} \right)^{1/2}(8x) dx $$ Simplify $$ = \frac{ \pi}{4} \left[ \frac{ \left( 1+4x^{2} \right)^{3/2}}{3/2} \right]_{0}^{\sqrt{2}} $$ Integrate $$ = \frac{ \pi}{6} \left[ (1+8)^{3/2}-1 \right] $$ $$ = \frac{ 13 \pi}{3} \approx 13.614$$

Internal Links

Parent Article: Calculus II 07 Integration Applications