Calculus II 10.03 Parametric Equations and Calculus

Previous	Calculus II 10.02 Plane Curves and Parametric Equations
Next	Calculus II 10.04 Polar Coordinates and Polar Graphs

10.3 Parametric Equations and Calculus

• Find the slope for a tangent line to a curve given by parametric equations.
• Find the arc length for a curve given by parametric equations.
• Find the area for a rotated surface in parametric form.

Slope and Tangent Lines

At time \(t\), the elevation angle is \(\theta\). Figure 10.3.1

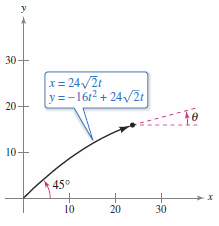
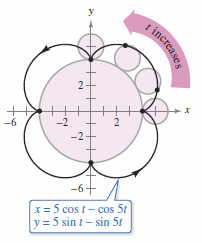
Consider the projectile represented by the parametric equations \(x=24\sqrt{2}t \text{ and } y=-16t^{2}+ 24\sqrt{2}t\) as shown in Figure 10.3.1. The initial angle is \(45^{\circ}\) with slope \(m=\tan 45^{\circ} = 1 \). Can the slope be found at any time \(t\)? Theorem 10.3.1 provides a formula for finding the slope as a function for \(t\).

Theorem 10.3.1 The Derivative for the Parametric Form

The slope for the secant line through the points \((f(t),g(t))\) and \((f(t+\Delta t),g(t+\Delta t))\) is \(\Delta y/ \Delta x\). Figure 10.3.2

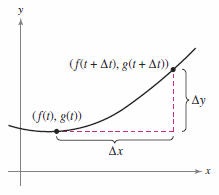
If a smooth curve \(C\) is given by the equations \(x=f(t) \text{ and } y=g(t)\) then the slope for \(C\) at a point is $$ \frac{dy}{dx} = \frac{dy/dt}{dx/dt},\: \frac{dx}{dt} \ne 0.$$ Proof Consider \(\Delta t >0\) and let \( \Delta x=f(t+\Delta t)-f(t) \text{ and } \Delta y=g(t+ \Delta t)-g(t) \) as shown in Figure 10.3.2. Because \(\Delta x \to 0\) as \(\Delta t \to 0\), the limit can be written as $$ \frac{dy}{dx} $$ $$= \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$ $$= \lim_{\Delta x \to 0} \frac{g(t+ \Delta t)-g(t)}{f(t+\Delta t)-f(t)} $$. Divide the numerator and denominator by \(\Delta t\) and differentiate for \(f\) and \(g\) to conclude. $$ \frac{dy}{dx} $$ $$=\lim_{\Delta x \to 0} \frac{[g(t+ \Delta t)-g(t)]\Delta t}{[f(t+\Delta t)-f(t)]/\Delta t} $$ $$= \frac{ \lim_{\Delta x \to 0}\frac{g(t+ \Delta t)-g(t)}{\Delta t} }{ \lim_{\Delta x \to 0} \frac{f(t+\Delta t)-f(t)}{\Delta t}} $$. $$= \frac{g{}^{\prime}(t)}{f{}^{\prime}(t)} = \frac{dy/dt}{dx/dt}.$$

Example 10.3.1 Differentiation and Parametric Form

Find \(dy/dx\) for the curve given by \(x=\sin t\) and \(y=\cos t\).
Solution

$$ \frac{dy}{dx} $$	$$= \frac{dy/dt}{dx/dt}$$
	$$= \frac{-\sin t}{\cos t} $$
	\(= - \tan t \)

Because \(dy/dx\) is a function for \(t\), Theorem 10.3.1 can be used repeatedly to find higher-order derivatives. For example,

$$ \frac{d^{2}y}{dx^{2}} = \frac{d}{dx} \left [ \frac{d}{dx} \right ] = \frac{ \frac{d}{dt} \left [ \frac{dy}{dx} \right ] }{dx/dt}$$	Second derivative
$$ \frac{d^{3}y}{dx^{3}} = \frac{d}{dx} \left [ \frac{d^{2}}{dx^{2}} \right ] = \frac{ \frac{d}{dt} \left [ \frac{d^{2}y}{dx^{2}} \right ] }{dx/dt} $$	Third derivative

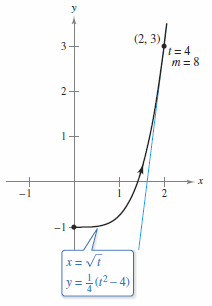
Example 10.3.2 Finding Slope and Concavity

The graph is concave upward at \((2,3)\) when \(t=4\). Figure 10.3.3

For the curve given by $$ x=\sqrt{t} \text{ and } y= \frac{1}{4}(t^{2}-4), \: t \geqslant 0 $$ find the slope and concavity at the \((2,3)\). Solution Because $$ \frac{dy}{dx}= \frac{dy/dt}{dx/dt} = \frac{(1/2)t}{(1/2)t^{-1/2}}=t^{3/2} \:\:\:\: \color{red}{\text{Parametric form for the first derivative }}$$ the second derivative is $$ \frac{d^{2}y}{dx^{2}}= \frac{\frac{d}{dt}[dy/dx]}{dx/dt} = \frac{\frac{d}{dt}[t^{3/2}]}{dx/dt} =\frac{(3/2)t^{1/2}}{(1/2)t^{-1/2}}=3t \:\:\:\: \color{red}{\text{Parametric form for the second derivative }}$$ At \((2,3)\) \(t=4\) and the slope is $$ \frac{dy}{dx}= (4)^{3/2}=8.$$ When \(t=4\) the second derivative is $$ \frac{d^{2}y}{dx^{2}}= 3(4)=12 >0.$$ The graph is concave upward at \((2,3)\) as shown in Figure 10.3.3.

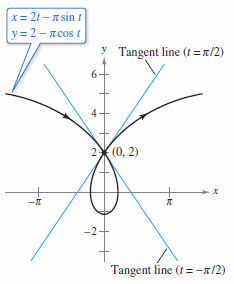
Example 10.3.3 A Curve with Two Tangent Lines at a Point

This prolate cycloid has two tangent lines at the point \((0,2)\). Figure 10.3.4

Because the parametric equations \(x=f(t)\) and \(y=g(t)\) need not define \(y\) as a function for \(x\), it is possible for a plane curve to loop around and cross itself. At these intersecting points, the curve may have more than one tangent line. The prolate cycloid[1] given by \( x=2t-\pi \sin t \text{ and } y=2 - \pi \cos t \) crosses itself at \((0,2)\), as shown in Figure 10.3.4. Find the equations for both tangent lines at this point. Solution Because \(x=0\) and \(y=2\) when \(t= \pm \pi /2\), and $$ \frac{dy}{dx}= \frac{dy/dt}{dx/dt} = \frac{\pi \sin t}{2-\pi \cos t}$$ This reduces to, \(dy/dx= - \pi /2 \) when \(t= - \pi /2 \) and \(dy/dx= \pi /2 \) when \(t= \pi /2 \). Therefore the tangent lines are $$ y-2= - \left (\frac{\pi}{2} \right )x \:\:\:\: \color{red}{\text{Tangent line when } t=-\frac{\pi}{2}} $$ $$ y-2= \left (\frac{\pi}{2} \right )x \:\:\:\: \color{red}{\text{Tangent line when } t=\frac{\pi}{2}}$$ The curve has a horizontal tangent at \((0,2-\pi)\) when \(t=0\). A vertical tangent occurs at \((f(t_{0}),g(t_{0}))\) whenever \(dx/dt=0\) and \(dy/dt \ne0\), when \(t=t_{0}\). A horizontal tangent occurs at \((f(t_{0}),g(t_{0}))\) whenever \(dy/dt=0\) and \(dx/dt \ne 0\), when \(t=t_{0}\).

Arc Length

How can the distance traveled by an object along parametric curve be determined? Recall from Section 7.4 that for a given curve \(C\) the formula for its arc length is given by \(y=h(x)\) over the interval \([x_{0},x_{1}]\) is

$$S$$	$$= \int_{x_{0}}^{x_{1}} \sqrt{ 1+ [h{}^{\prime}(x)]^{2} }\: dx $$
	$$= \int_{x_{0}}^{x_{1}} \sqrt{ 1+ \left ( \frac{dy}{dx} \right)^{2} }\: dx $$
If \(C\) is represented by the parametric equations \(x=f(t)\) and \(y=g(t)\), \(a \leqslant t \leqslant b\), and if \(dx/dt={f{}^{\prime}(t)} >0\), then the equation continues
	$$= \int_{x_{0}}^{x_{1}} \sqrt{ 1+ \left ( \frac{dy/dt}{dx/dt} \right)^{2} }\: dx $$
	$$= \int_{a}^{b} \sqrt{ \frac{(dx/dt)^{2}+(dy/dt)^{2}}{(dx/dt)^{2}} }\: \frac{dx}{dt}\: dt $$
	$$= \int_{a}^{b} \sqrt{ \left( \frac{dx}{dt}\right)^{2}+\left( \frac{dy}{dt}\right)^{2}}\: dt $$
	$$= \int_{a}^{b} \sqrt{[ f{}^{\prime}(t)]^{2}+[ g{}^{\prime}(t)]^{2}}\: dt. $$

Theorem 10.3.2 Arc Length in Parametric Form

If a smooth curve \(C\) is represented by the parametric equations \(x=f(t)\) and \(y=g(t)\) such that \(C\) doe snot intersect itself over the interval \(a \leqslant t \leqslant b\), except possibly at the endpoints, then the arc length for \(C\) over that interval is given by

$$S = \int_{a}^{b} \sqrt{ \left( \frac{dx}{dt}\right)^{2}+\left( \frac{dy}{dt}\right)^{2}}\: dt = \int_{a}^{b} \sqrt{[ f{}^{\prime}(t)]^{2}+[ g{}^{\prime}(t)]^{2}}\: dt. $$

Example 10.3.4 Finding the Arc Length for a Epicycloid

An epicycloid is traced by a point on the smaller circle as it rolls around the larger circle. Figure 10.3.5

An epicycloid[2] is traced by a point on the smaller circle as it rolls around the larger circle. A circle, with radius 1, rolls around a circle, with radius 4, as shown in Figure 10.3.5. The epicycloid is given by \( x= 5 \cos t-\cos 5t \text{ and } y=5 \sin t - \sin 5t. \) Find the distance traveled by the point in one complete trip about the larger circle. Solution Before applying Theorem 10.3.2, note in Figure 10.3.5 that the curve has sharp points when \(t=0\) and \(t=\pi/2\). Between these two points, \(dx/dt\) and \(dy/dt\) are not simultaneously 0. The curve segment generated from \(t=0\) to \(t=\pi/2\) is smooth. To find the total distance traveled by the point,find the arc length for the segment in the first quadrant and multiply by 4. $$S$$ $$= 4\int_{0}^{\pi/2} \sqrt{ \left( \frac{dx}{dt}\right)^{2}+\left( \frac{dy}{dt}\right)^{2}}\: dt \:\:\:\: \color{red}{\text{Parametric form for arc length }} $$ $$= 4\int_{0}^{\pi/2} \sqrt{ \left( -5 \sin t + 5 \sin 5t \right)^{2}+\left( 5 \cos t-5 \cos 5t\right)^{2}}\: dt $$ $$= 20\int_{0}^{\pi/2} \sqrt{ 2-2 \sin t \sin 5t - 2 \cos t \cos 5t}\: dt $$ $$= 20\int_{0}^{\pi/2} \sqrt{ 2- \cos 4t}\: dt \:\:\:\: \color{red}{\text{Difference formula for cosine }}$$ $$= 20\int_{0}^{\pi/2} \sqrt{ 4 \sin^{2} 2t}\: dt \:\:\:\: \color{red}{\text{Double-angle formula }}$$ $$= 40\int_{0}^{\pi/2} \sin 2t\: dt $$ $$= -20 \bigg[ \cos 2t \bigg]_{0}^{\pi/2} = 40 $$ For the epicycloid shown in Figure 10.3.5, an arc length 40 long seems about right because the circle's circumference with radius 6 is \(2 \pi r = 12 \pi \approx 37.7\).

Area for a Rotated Surface

The formula for a rotated surface area in rectangular form to develop a formula for a rotated surface area in parametric form.

Theorem 10.3.3 Area for a Rotated Surface in Parametric Form

If a smooth curve \(C\) given by \(x=f(t)\) and \(y=g(t)\) does not cross itself on an interval \(a \leqslant t \leqslant b\), then the area \(S\) for the rotated surface formed by revolving \(C\) about the coordinate axis is given by the following.

$$1. \:S= 2 \pi\int_{a}^{b} g(t) \sqrt{ \left( \frac{dx}{dt}\right)^{2}+\left( \frac{dy}{dt}\right)^{2}}\: dt \:\:\:\: \color{red}{\text{Revolution about the }x\text{-axis: }g(t) \geqslant 0} $$

$$2. \:S= 2 \pi\int_{a}^{b} f(t) \sqrt{ \left( \frac{dx}{dt}\right)^{2}+\left( \frac{dy}{dt}\right)^{2}}\: dt \:\:\:\: \color{red}{\text{Revolution about the }y\text{-axis: }f(t) \geqslant 0} $$

The differential form for the arc length is

$$ds= \sqrt{ \left( \frac{dx}{dt}\right)^{2}+\left( \frac{dy}{dt}\right)^{2}}\: dt$$

Then the formulas are written as

$$1. \:S= 2 \pi \int_{a}^{b} g(t)\: ds \:\:\:\: 2.\: S= 2 \pi \int_{a}^{b} f(t)\:ds $$

Example 10.3.5 Finding the Area for a Rotated Surface

An epicycloid is traced by a point on the smaller circle as it rolls around the larger circle. Figure 10.3.6

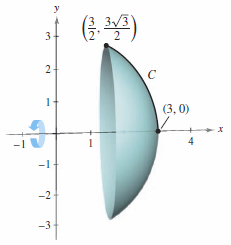
Let \(C\) be the arc for the circle \(x^{2}+y^{2}=9\) between $$(3,0) \text{ and } \left ( \frac{3}{2}, \frac{3\sqrt{3}}{2} \right ) $$ as shown in Figure 10.3.6. Find the area for the surface formed by rotating \(C\) about the \(x\)-axis. Solution The curve \(C\) can be represented parametrically by the equations \(x= 3 \cos t \text{ and } y = 3 \sin t, \: 0 \leqslant t \leqslant \pi /3. \) The interval for \(t\) was determined by observing that \(t=0\) when \(x=3\) and \(t=\pi /3 \) when \(x=3/2\). On this interval, \(C\) is smooth and \(y\) is nonnegative, and Theorem 10.3.3 can be applied. $$S$$ $$=2 \pi \int_{0}^{\pi/3} (3 \sin t) \sqrt{(-3 \sin t)^{2}+(3 \cos t)^{2}} \:dt $$     Theorem 10.3.3 $$=6 \pi \int_{0}^{\pi/3} \sin t \sqrt{9(-3 \sin t)^{2}+(3 \cos t)^{2}} \:dt $$ $$=6 \pi \int_{0}^{\pi/3} 3 \sin t \:dt $$     Trigonometric identity $$=-18 \pi \bigg[ \cos t \bigg]_{0}^{\pi/3} $$ $$=-18 \pi \left( \frac{1}{2}-1 \right)= 9\pi $$

Internal Links

Parent Article: Calculus II 10 Conics Parametric Equations and Polar Coordinates