Calculus I 01.05 Infinite Limits

Previous	Calculus I 01.04 Continuity and One-Sided Limits
Next	Calculus I 02 Differentiation

Infinite Limits

• Determine infinite limits from the left and from the right.
• Find and sketch the vertical asymptotes for a function graph.

\(f(x)\) increases and decreases without bound as \(x\) approaches 2. Figure 1.5.1

Consider the function \(f(x)=3/(x-2)\). From Figure 1.5,1 and Table 1.5.1, \(f(x)\) decreases without bound as \(x\) approaches 2 from the left, and \(f(x)\) increases without bound as \(x\) approaches 2 from the right. Table 1.5.1 This behavior is denoted as $$ \lim_{x \to 2^- } \frac{3}{x-2} = -\infty$$     \(f(x)\) decreases with bound as \(x\) approaches 2 from the left. as $$ \lim_{x \to 2^+ } \frac{3}{x-2} = \infty.$$     \(f(x)\ increases without bound as \(x\) approaches 2 from the right. The symbols \(\infty\) and \(-\infty\) refer to positive infinity and negative infinity, respectively. These symbols do not represent real numbers. They are convenient symbols used to describe unbounded conditions more concisely. A limit in which \(f(x)\) increases or decreases without bound as \(x\) approaches \(c\) is called an infinite limit.

Definition 1.5.1 Infinite Limits

Infinite Limits Figure 1.5.2

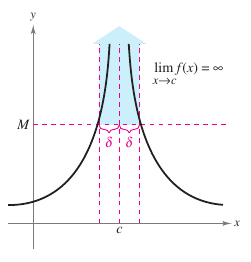
Let \(f\) be a function that is defined at every real number on some open interval containing \(c\) (except possibly at \(c\) itself.) The statement $$ \lim_{x \to c} f(x) = \infty $$ means that for each \(M >0\) there exists a \(\delta > 0\) such that \(f(x)>M\) whenever \(0< |x-c|< \delta\), as shown in Figure 1.5.2. Similarly, the statement $$ \lim_{x \to c} f(x) = -\infty $$ means that for each \(N<0\) there exists a \(\delta >0\) such that \(f(x)<N\) whenever \(0<|x-c| < \delta.\) To define the infinite limit from the left, replace \(0<|x-c| < \delta\) by \(c-\delta<x<c\). To define the infinite limit from the right, replace \(0<|x-c| < \delta\) by \(c<x<c+\delta\). The equal sign in the statement \(\lim f(x)=\infty\) does not mean that the limit exists. It states the limit fails to exist by denoting the \(f(x)\)'s unbounded behavior \(x\) approaches \(c\).

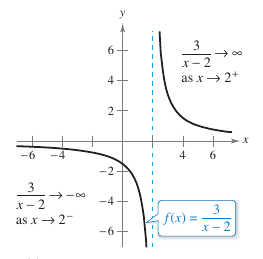
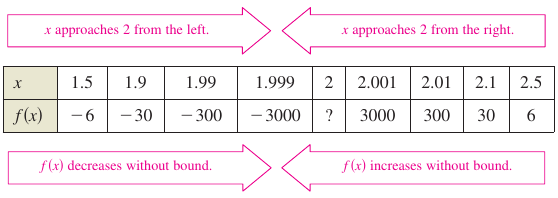
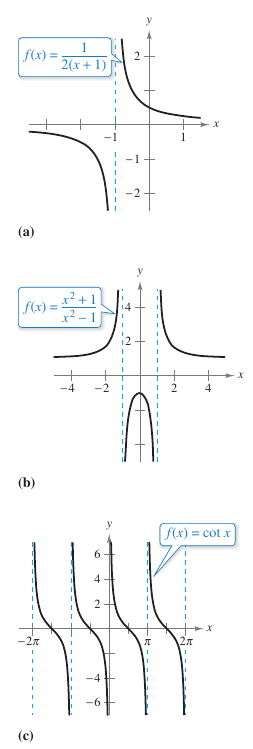
Example 1.5.1 Determining Infinite Limits from a Graph

Determine the limit for each function shown in Figure 1.5.3 as \(x\) approaches 1 from the left and from the right.

Each graph has an asymptote at \(x=1\).
Figure 1.5.3

Solution

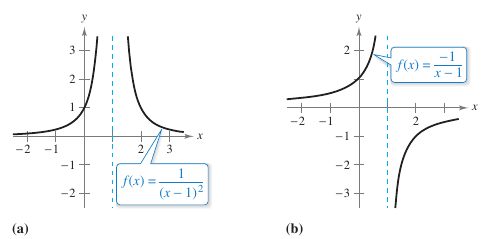
a.	When \(x\) approaches 1 from the left or right, \((x-1)^2\) is a small positive number. Therefore,the quotient \(1/(x-1)^2\) is a large positive number, and \(f(x)\) approaches infinity from each side of \(x=1\). To conclude that $$\lim_{x \to 1} \frac{1}{(x-1)^2} = \infty.$$     Limit from each side is infinity.
	Figure 1.5.3(a) confirms this analysis.
b.	When \(x\) approaches 1 from the left, \(x-1\) is a small negative number. Therefore, the quotient \(-1/(x-1)\) is a large negative number, and \(f(x)\) approaches negative infinity from the right of \(x=1\). To conclude that $$\lim_{x \to 1^-} \frac{-1}{x-1} = \infty.$$     Limit from the left side is infinity.
	When \(x\) approaches 1 from the right, \(x-1\) is a small positive number. Therefore, the quotient \(-1/(x-1)\) is a large negative number, and \(f(x)\) approaches negative infinity from the right of \(x=1\). To conclude that $$\lim_{x \to 1^+} \frac{-1}{x-1} = -\infty.$$     Limit from the right side is negative infinity.
	Figure 1.5.3(b) confirms this analysis.

Vertical Asymptotes

Functions with vertical asymptotes Figure 1.5.4

If it were possible to extend the graphs in Figure 1.5.2 toward positive and negative infinity each graph becomes arbitrarily close to the vertical line \(x=1\). This line is a vertical asymptote for \(f\). Other asymptotes are described in Sections 3.5 and 3.6. Definition 1.5.2 Vertical Asymptotes If \(f(x)\) approaches positive or negative infinity as \(x\) approaches \(c\) from the right or left, then the line \(x=c\) is a vertical asymptote for \(f\). If \(f\) has a vertical asymptote at \(x=c\), then \(f\) is not continuous at \(c\). In Example 1.5.1 note that each functions is a quotient and that each vertical asymptote occurs at a number at which the denominator is 0 (and the numerator is not 0). Theorem 1.5.1 generalizes this observation. Theorem 1.5.1 Vertical Asymptotes Let \(f\) and \(g\) be continuous on an open interval containing \(c\). If \(f(c)\neq 0\), \(g(c)=0\), and there exists an open interval containing \(c\) such that \(g(c) \neq 0\) for all \(x \neq c\) on the interval, then the graph for $$ h(x)=\frac{f(x)}{g(x)}$$ has a vertical asymptote at \(x=c\). Example 1.5.2 Finding Vertical Asymptotes a. When \(x=-1\), the denominator for $$ f(x)=\frac{1}{2(x+1)}$$ is 0 and the numerator is not 0. By Theorem 1.5.1 \(x=-1\) is a vertical asymptote, as shown in Figure 1.5.4(a). b. By factoring the denominator as $$f(x)=\frac{x^2+1}{x^2-1} = \frac{x^2+1}{(x-1)(x+1)}$$ the result is 0 at \(x=-1\) and \(x=1\). Because the numerator is not 0 at these two points, apply Theorem 1.5.1 to conclude that \(f\) has two vertical asymptotes, as shown in Figure 1.5.4(b). c. By writing the cotangent function in the form $$f(x)=\cot x= \frac{\cos x}{\sin x}$$ Theorem 1.5.1 can be applied to conclude that vertical asymptotes occur at all values for \(x\) such that \(\sin x=0\) and \(\cos x \neq 0\), as shown in Figure 1.5.4(c). The graph for this function has infinitely many vertical asymptotes. They occur at \(x=n\pi\) where \(n\) is an integer.

Theorem 1.5.1 requires the numerator value for \(x=c\) be nonzero. When both the numerator and denominator are 0 at \(x=c\) an indeterminate form \(0/0\) is produced. The limit's behavior at \(x=c\) can not be determined without further investigation, as described in Example 1.5.3.

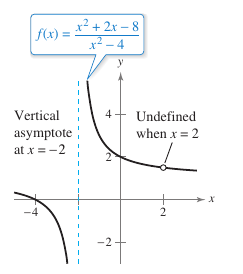
Example 1.5.3 A Rational Function with Common Factors

\(f(x)\) increases and decreases without bound as \(x\) approaches -2. Figure 1.5.5

For \(f(x)\)'s graph determine all vertical asymptotes. $$ f(x)=\frac{x^2+2x-8}{x^2-4}.$$ Solution Begin by simplifying the expression $$f(x)$$ $$=\frac{x^2+2x-8}{x^2-4}$$ $$=\require{cancel}\frac{(x+4)\cancel{(x-2)}}{(x+2)\cancel{(x-2)}}$$ $$=\frac{(x+4)}{(x+2)}, \:\:\:\: x \neq 2.$$ Let \(g(x)\) represent the simplified expression. The graphs for \(f(x)\) and \(g(x)\) coincide at all \(x\)-values other than \(x=2\). Applying Theroem 1.5.1 to \(f\) and \(g\) produces a vertical asymptote at \(x=-2\), as shown in Figure 1.5.5. From the graphs the limit is $$ \lim_{x \to 2^-} \frac{x^2+2x-8}{x^2-4} = -\infty \text{ and } \lim_{x \to 2^+}\frac{x^2+2x-8}{x^2-4}= \infty.$$ Note that \(x=2\) is not a vertical asymptote.

Example 1.5.4 Determining Infinite Limits

\(f\) has a vertical asymptote at \(x=1\). Figure 1.5.6

Find each limit. $$ \lim_{x \to 1^-} \frac{x^2-3x}{x-1} \text{ and } \lim_{x \to 1^+}\frac{x^2-3x}{x-1} $$ Solution Because the denominator is 0 when \(x=1\) and the numerator is not zero, the graph for $$f(x)=\frac{x^2-3x}{x-1}$$ has a vertical asymptote at \(x=1\). This means that each limit is either \(\infty\) or \(-\infty\). Figure 1.5.6 shows the graph for \(f\) has an asymptote at \(x=1\) and approaches \(\infty\) from the left and approaches \(-\infty\) from the right. The answer is $$ \lim_{x \to 1^-} \frac{x^2-3x}{x-1}$$     The limit from the left is infinity. and $$\lim_{x \to 1^+}\frac{x^2-3x}{x-1} $$     The limit from the right is negative infinity.

Theorem 1.5.2 Infinite Limits Properties

Let \(c\) and \(L\) be real numbers. Let \(f\) and \(g\) be functions such that

$$ \lim_{x \to c} f(x) = \infty \text{ and } \lim_{x \to c} g(x) =L.$$

1. Sum or difference:	$$ \lim_{x \to c} [f(x) \pm g(x)] = \infty$$
2. Product:	$$ \lim_{x \to c} [f(x) g(x)] = \infty, \:\:\:\: L>0$$
	$$ \lim_{x \to c} [f(x) \pm g(x)] = -\infty, \:\:\:\: L<0$$
3. Quotient:	$$ \lim_{x \to c} \frac{g(x)}{f(x)}=0$$

Similar properties hold for one-sided limits and for functions where the limit for \(f(x)\) as \(x\) approaches \(c\) is \(-\infty\) as shown in Example 1.5.5(d).
Proof This is a proof for the Sum property. Proofs for the other properties are similar. To show that the limit for \(f(x)+g(x)\) is infinite, choose \(M>0\). Then find \(\delta >0\) such that \([f(x)+g(x)]>M\) whenever \(0<|x-c|<\delta\). Simplify by assuming \(L\) is positive. Let \(M_1=M+1\). Because the limit for \(f(x)\) is infinite, there exists \(\delta_1\) such that \(f(x)>M_1\) whenever \(0<|x-c|<\delta_1\). Because \(L\) is the limit for \(g(x)\) there exists \(\delta_2\) such that \(|g(x)-L|<1\) whenever \(0<|x-c|<\delta_2\). By letting \(\delta\) be smaller than \(\delta_1\) and \(\delta_2\), the conclusion is that \(0<|x-c|<\delta\) implies \(f(x)>M+1\) and \(|g(x)-L|<1\). The second inequality implies that \(g(x)>L-1\). Adding the inequalities produces

\(f(x)+g(x)>(M+1)+(L-1)=M+L>M\).

Thus,

$$ \lim_{x \to c} [f(x) \pm g(x)] = \infty$$

Example 1.5.5 Determining Limits

a.	Because \(\lim_{x \to 0} 1=1\) and \(\lim_{x \to 0} \frac{1}{x^2}, the expression can be written as
	$$ \lim_{x \to 0} \left ( 1+\frac{1}{x^2} \right )= \infty$$     Theorem 1.5.2, Property 1.
b.	Because \(\lim_{x \to 1^-} (x^2+1)=2\) and \(\lim_{x \to 1^-} (\cot \pi x) = -\infty\), the expression can be written as
	$$ \lim_{x \to 1^-} \frac{x^2+1}{\cot \pi x} = 0 $$     Theorem 1.5.2, Property 3.
c.	Because \(\lim_{x \to 0^+} 3=3\) and \(\lim_{x \to 0^+} \cot x = \infty\), the expression can be written as
	$$ \lim_{x \to 0^+} 3 \cot x = \infty$$     Theorem 1.5.2, Property 2.
d.	Because \(\lim_{x \to 0^-} x^2=0\) and \(\lim_{x \to 0^-} \frac{1}{x} = -\infty\), the expression can be written as
	$$ \lim_{x \to 0^-} \left ( x^2+\frac{1}{x} \right )= -\infty$$     Theorem 1.5.2, Property 1.

Internal Links

Parent Article: Calculus I 01 Limits and Their Properties