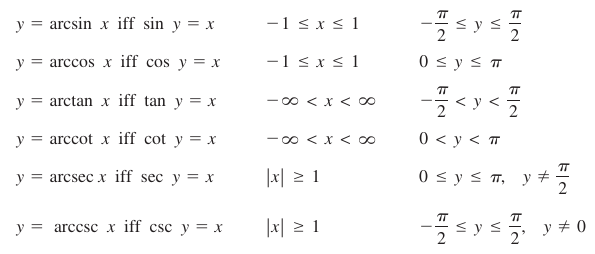Calculus I 05.06 Inverse Trigonometric Functions: Differentiation

Previous	Calculus I 05.05 Bases Other than e and Applications
Next	Calculus I 05.07 Inverse Trigonometric Functions: Integration

• Properties for the six inverse trigonometric functions.
• Differentiate an inverse trigonometric function.
• Review the basic differentiation rules for elementary functions.

Inverse Trigonometric Functions

The sine function is one-to-one on \([-\pi/2,\pi/2]\). Figure 5.6.1

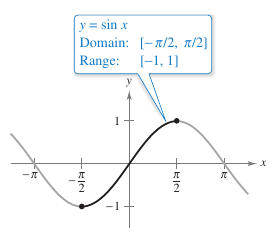
The six basic trigonometric functions do not have an inverse function. This statement is true because they are all periodic and therefore are not one-to-one. The discussion now examines these six functions to see whether their domains can be restricted in such a way that they will have inverse functions on limited domains. The sine function is increasing, and therefore is one-to-one, on the interval $$\left [ -\frac{\pi}{2},\frac{\pi}{2} \right ]$$ as shown in Figure 5.6.1. 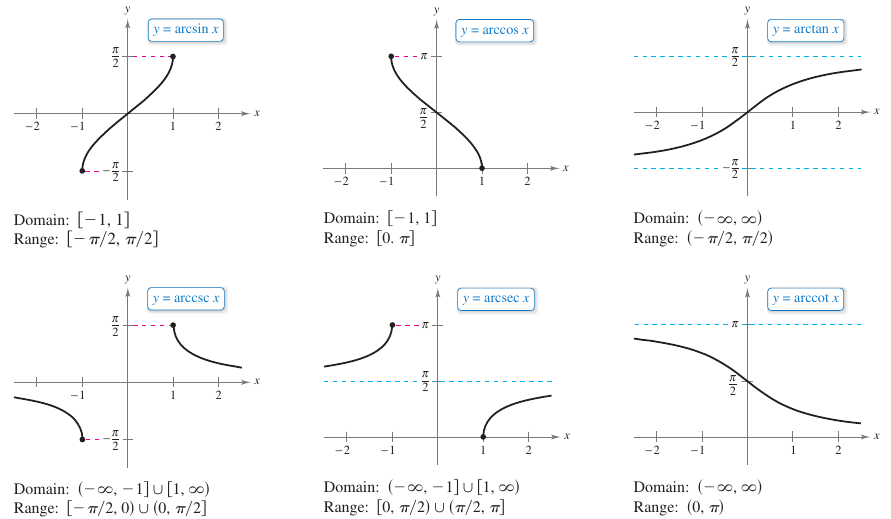On this interval define the inverse for the restricted sine function as \(y=\arcsin x \:\:\text{if and only if}\: \sin y = x\) where \(-1 \leq x \leq 1 \) and \( - \pi/2 \leq \arcsin x \leq \pi/2\). Under suitable restrictions, each trigonometric function is one-to-one and so has an inverse function, as shown in Definition 5.6.1. Note that the term “iff” is used to represent the phrase “if and only if.”

Definition 5.6.1 Inverse Trigonometric Functions

The term “arcsin x” is read as “the arcsine for x” or sometimes “the angle whose sine is x.” An alternative notation for the inverse sine function is “\(sin^{-1} x\)”.

Graphs for the six trigonometric functions.
Figure 5.6.2

Evaluating inverse trigonometric functions produce angles measured in radians.

Example 5.6.1 Evaluating Inverse Trigonometric Functions

Evaluate each function.

a.

$$\arcsin \left ( - \frac{1}{2} \right )$$

b.

\(\arccos 0\)

c.

\(\arctan \sqrt{3}\)

d.

\( \arcsin (0.3)\)

Solution a. By definition, \(y = \arcsin \left (-\frac{1}{2} \right ) \) implies that \(\sin y =-\frac{1}{2}\). In the interval \([-\pi/2, \pi/2]\), the correct value for \(y\) is \(-\pi/6\).

$$ \arcsin \left ( -\frac{1}{2} \right ) = - \frac{\pi}{6}$$

b. By definition, \(y= \arccos 0 \) implies that \(\cos y = 0\). In the interval \([0,\pi]\), \(y=\pi/2\).

$$ \arccos 0 = \frac{\pi}{2}$$

c. By definition, \(y= \arctan \sqrt{3}\) implies that \(\tan y = \sqrt{3}\). In the interval \((-\pi/2, \pi/2)\), \(y=\pi/3\).

$$ \arctan \sqrt{3}=\frac{\pi}{3}$$

d. Using a computer displaying radians produces

\( \arcsin (0.3) \approx 0.305\).

Inverse functions have the properties \(f(f^{-1}(x))=x\) and \(f^{-1}(f(x))=x\). When applying these properties to inverse trigonometric functions, remember the trigonometric functions have inverse functions only on restricted domains. For \(x\)-values outside these domains, these properties do not hold. For example, \(\arcsin (\sin x)\) is equal to \(0\), not \(\pi\).

Inverse Trigonometric Function Properties

If \(-1 \leq x \leq 1\) and \(-\pi/2 \leq y leq \pi/2\), then

\(\sin (\arcsin x) = x\) and \(\arcsin (\sin y)=y.\)

If \(-\pi/2 < y < \pi/2\), then

\( \tan (\arctan x )=x\) and \(\arctan (\tan y)=y.\)

If \( \left | x \right | \leq 1\) and \(0 \leq y < \pi/2\) or \(\pi/2 < y \leq \pi\), then

\( \sec ( \operatorname{arcsec} x ) = x\) and \(\operatorname{arcsec} ( \sec y) = y\).

Similar properties hold for the other inverse trigonometric functions.

Example 5.6.2 Solving an Inverse Trigonometric Function

$$\:\:\:\arctan (2x-3)$$	$$= \frac{\pi}{4}$$	Original equation
$$\tan \left [ \arctan (2x-3) \right ]$$	$$= \tan \frac{\pi}{4}$$	Take tangent from each side
\(\:\:\: 2x-3\)	\(=1\)	\( \tan ( \arctan x) = x\)
\(\:\:x\)	\(=2\)	Solve for \(x\)

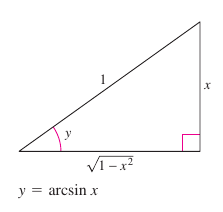
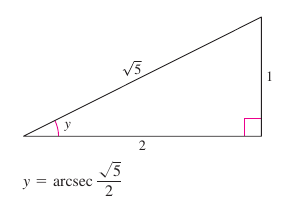
Example 5.6.3 Using Right Triangles

Figure 5.6.3 Figure 5.6.4

Evaluate the following as \(\cos (\arcsin x) \). a. Given \(y=\arcsin x\), where \(0 < y < \pi/2\), find \(\cos y\). b. Given \(y=\operatorname{arcsec} \left ( \sqrt{5}/2 \right )\), find \(\tan y\). Solution a. Because \(y=\arcsin x\), then \(\sin y=x\). This relationship between \(x\) and \(y\) can be expressed by a right triangle, as shown in Figure 5.6.4. $$ \cos y = \cos (\arcsin x ) = \frac{\text{adj.}}{\text{hyp.}}= \sqrt{1-x^2}$$ This result is also valid for \(-\pi/2 < y < 0\). b. The right triangle in Figure 5.6.5 shows a similar relationship between \(y=\operatorname{arcsec} \left ( \sqrt{5}/2 \right )\) and \(\tan y\). $$\tan y $$ $$=\tan \left [ \operatorname{arcsec} \left ( \frac{\sqrt{5}}{2} \right ) \right ]$$ $$=\frac{\text{opp.}}{\text{adj.}}$$ $$=\frac{1}{2}$$

Inverse Trigonometric Function Derivatives

Section 5.1 discussed the derivative for the transcendental function \(f(x)= \ln x\) is the algebraic function \({f}'(x)=1/x\). The derivatives for the inverse trigonometric functions are also algebraic. This is true even though the inverse trigonometric functions are themselves transcendental.

Theorem 5.6.1 lists derivatives for the six inverse trigonometric functions. Note the derivatives for \(\arccos u\). \(\operatorname{arccot} u\), and \(\operatorname{arcsec} u\) are the negatives for the derivatives for \(\arcsin u\), \(\arctan u\), and \(\operatorname{arcsec} u\), respectively.

Theorem 5.6.1 Inverse Trigonometric Function Derivatives

Let \(u\) be a differentiable function for \(x\).

$$\frac{d}{dx} [\arcsin u]= \frac{{u}'}{\sqrt{1-u^2}}$$	$$\frac{d}{dx} [\arccos u]= \frac{-{u}'}{\sqrt{1-u^2}}$$
$$\frac{d}{dx} [\arctan u]= \frac{{u}'}{1+u^2}$$	$$\frac{d}{dx} [\operatorname{arccot} u]= \frac{-{u}'}{1+u^2}$$
$$\frac{d}{dx} [\operatorname{arcsec} u]= \frac{{u}'}{|u|\sqrt{u^2-1}}$$	$$\frac{d}{dx} [\operatorname{arcsec} u]= \frac{-{u}'}{|u|\sqrt{u^2-1}}$$

There is no common agreement on the definition for \(\operatorname{arcsec} x\) or \(\operatorname{arccsc} x\) for negative \(x\)-values. When the \(\operatorname{arcsecant}\)'s range was defined the reciprocal identity was preserved

$$ \operatorname{arcsec} x = \arccos \frac{1}{x}.$$

One consequence is its graph has a positive slope at every \(x\)-value in its domain, as shown in Figure 5.6.2. This accounts for the absolute value sign in the formula for the \(\operatorname{arcsec} x\) derivative.

Example 5.6.4 Differentiating Inverse Trigonometric Functions

If the graphing utility does not have the \(\operatorname{arcsecant}\) function, the expression

$$f(x)=\operatorname{arcsec} x=\operatorname{arccos}\frac{1}{x}$$

produces it.

Example 5.6.5 A Derivative That Can Be Simplified

\(y\)	\(=\arcsin x + x\sqrt{1-x^2}\)
$${y}'$$	$$=\frac{1}{\sqrt{1-x^2}} + x \left ( \frac{1}{2} \right )(-1x)(1-x^2)^{-1/2}+\sqrt{1-x^2}$$
	$$=\frac{1}{\sqrt{1-x^2}} - \frac{x^2}{\sqrt{1-x^2}}+\sqrt{1-x^2}$$
	\(=\sqrt{1-x^2} + \sqrt{1-x^2}\)
	\(=2\sqrt{1-x^2}\)

Example 5.6.5 demonstrates a benefit for inverse trigonometric functions, they are useful in integrating common algebraic functions. The result from Example 5.6.5 implies that,

$$ \int \sqrt{1-x^2}\:dx= \frac{1}{2} \left ( \arcsin x + x\sqrt{1-x^2}\right).$$

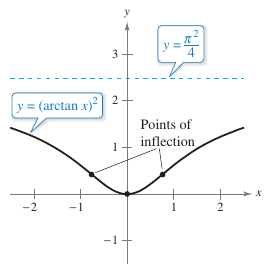
Example 5.6.6 Analyzing an Inverse Trigonometric Graph

The graph for \(y=(\arctan x)^2\) has a horizontal asymptote at \(y=\pi^2/4\). Figure 5.6.5

Analyze the graph for \(y=(\arctan x)^2\) Solution From the derivative $${y}'$$ $$=2( \arctan x) \left ( \frac{1}{1+x^2} \right )$$ $$=\frac{2 \arctan x}{1+x^2},$$ implies the only critical number is \(x=0\). By the First Derivative Test, this value is a relative minimum. From the second derivative $${y}''$$ $$\frac{(1+x^2)\left ( \frac{2}{1+x^2} \right )- (2 \arctan x)(2x)}{(1+x^2)^2}$$ $$=\frac{2(1-2x \arctan x)}{(1+x^2)^2}$$ it follows the inflection points occur when \(2 x \arctan x=1\). Using Newton's Method, these points occur when \(x \approx \pm 0.765\). Because $$\lim_{x \to \infty} \left ( \arctan x \right )^2= \frac{\pi^2}{4}$$ if follow that the graph has a horizontal asymptote at \(y= \pi^2/4\), as shown in Figure 5.6.5.

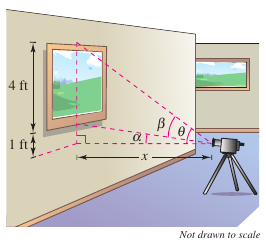
Example 5.6.7 Maximizing an Angle

The camera should be 2.236 feet from the painting to maximize the angle \(\beta\). Figure 5.6.6

A photographer is taking a shooting a painting hung in an art gallery. The painting is 4 feet high. The camera lens is 1 foot below the lower painting edge, as shown in Figure 5.6.6. How far should the camera be from the painting to maximize the angle subtended by the camera lens? Solution In Figure 5.6.6, let \(\beta\) be the angle maximized. \(\beta\) \(= \theta - \alpha\) $$= \operatorname{arccot} \frac{x}{5} - \operatorname{arccot} x$$ Differentiating produces $$\frac{d \beta}{dx}$$ $$=\frac{-1/5}{ 1+(x^2/25)}- \frac{-1}{1+x^2}$$ $$=\frac{-5}{25+x^2} +\frac{1}{1+x^2}$$ $$=\frac{4(5-x^2)}{(25+x^2)(1+x^2)}.$$ Because \(d\beta/dx=0\) when \(x=\sqrt{5}\), conclude from the First Derivative Test that this distance yields a maximum value for \(\beta\). Therefore, the distance is \(x \approx 2.236\) feet and the angle is \(\beta \approx 0.7297\) radian \(\approx 41.81\)°.

Basic Differentiation Rules Review

In the 1600s, Europe was ushered into the scientific age by such great thinkers as Descartes, Galileo, Huygens, Newton, and Kepler. These men believed that nature is governed by basic laws—laws that can, for the most part, be written in mathematical equations. One influential publication during this period, Dialogue on the Great World Systems[1], by Galileo Galilei is a classic in modern scientific thought.

As mathematics has developed during the past four hundred years, a few elementary functions have proven sufficient for modeling most phenomena in physics, chemistry, biology, engineering, economics, and many other fields. An elementary function is a function from the following list or one that can be formed as the sum, product, quotient, or composition of functions in the list.

Table 5.6.1
Algebraic Functions	Transcendental Functions
Polynomial functions	Logarithmic functions
Rational functions	Exponential functions
Functions involving radicals	Trigonometric functions
	Inverse trigonometric functions

Every elementary function can be differentiated with the rules introduced so far in the discussion. For convenience, these differentiation rules are summarized below.

Basic Differentiation Rules for Elementary Functions

Internal Links

Parent Article: Calculus I 05 Logarithmic, Exponential, and Other Transcendental Functions