Calculus III Advanced (Course) (11.4) (Homework)

Section 11.4 Homework

From Calculus 10e by Larson and Edwards, p. 781. Exercises 1, 2, 3, 4, 5, 6, 10, 16, 28, 38.

Exercises 11.4.1 - 6 Cross Product for Unit Vectors

1.	\(\textbf{j} \times \textbf{i} \)	1.	\(\textbf{i} \times \textbf{j} \)	3.	\(\textbf{j} \times \textbf{k} \)
4.	\(\textbf{k} \times \textbf{j} \)	5.	\(\textbf{i} \times \textbf{k} \)	6.	\(\textbf{k} \times \textbf{i} \)

Solution
The unit vectors are: \(\textbf{i} = \langle 1,0,0 \rangle \), \(\textbf{j} = \langle 0,1,0 \rangle \), and \(\textbf{k} = \langle 0,0,1 \rangle \).

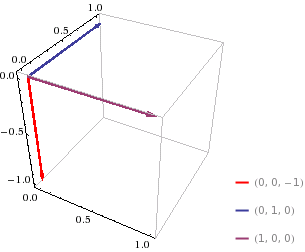Figure 11.4.1

$$ \textbf{1. } \textbf{j} \times \textbf{i} $$ $$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{vmatrix} $$ \(= \begin{vmatrix} 1 & 0 \\ 0 & 0 \end{vmatrix} \textbf{i} - \begin{vmatrix} 0 & 0 \\ 1 & 0 \end{vmatrix} \textbf{j} + \begin{vmatrix} 0 & 1 \\ 1 & 0 \end{vmatrix} \textbf{k} \) \(= (0-0)\textbf{i} -(0-0)\textbf{j}+(0-1)\textbf{k} \) \(= 0\textbf{i} + 0\textbf{j} - 1\textbf{k} \)

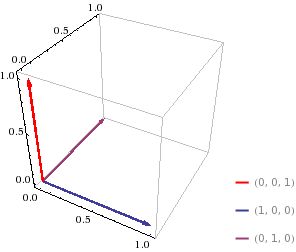Figure 11.4.2

$$ \textbf{2. } \textbf{i} \times \textbf{j} $$ $$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{vmatrix} $$ \(= \begin{vmatrix} 0 & 0 \\ 1 & 0 \end{vmatrix} \textbf{i} - \begin{vmatrix} 1 & 0 \\ 0 & 0 \end{vmatrix} \textbf{j} + \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} \textbf{k} \) \(= (0-0)\textbf{i} -(0-0)\textbf{j}+(1-0)\textbf{k} \) \(= 0\textbf{i} + 0\textbf{j} + 1\textbf{k} \)

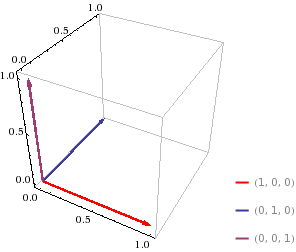Figure 11.4.3

$$ \textbf{3. } \textbf{j} \times \textbf{k} $$ $$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} $$ \(= \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} \textbf{i} - \begin{vmatrix} 0 & 0 \\ 0 & 1 \end{vmatrix} \textbf{j} + \begin{vmatrix} 0 & 1 \\ 0 & 0 \end{vmatrix} \textbf{k} \) \(= (1-0)\textbf{i} -(0-0)\textbf{j}+(0-0)\textbf{k} \) \(= 1\textbf{i} + 0\textbf{j} + 0\textbf{k} \)

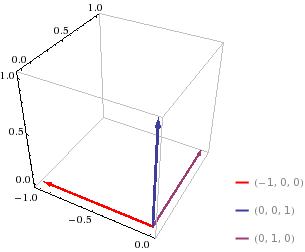Figure 11.4.4

$$ \textbf{4. } \textbf{k} \times \textbf{j} $$ $$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{vmatrix} $$ \(= \begin{vmatrix} 0 & 1 \\ 1 & 0 \end{vmatrix} \textbf{i} - \begin{vmatrix} 0 & 1 \\ 0 & 0 \end{vmatrix} \textbf{j} + \begin{vmatrix} 0 & 0 \\ 0 & 1 \end{vmatrix} \textbf{k} \) \(= (0-1)\textbf{i} -(0-0)\textbf{j}+(0-0)\textbf{k} \) \(= -1\textbf{i} + 0\textbf{j} + 0\textbf{k} \)

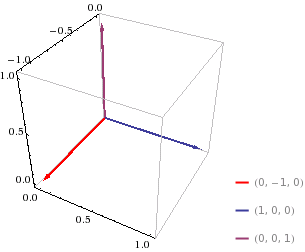Figure 11.4.5

$$ \textbf{5. } \textbf{i} \times \textbf{k} $$ $$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{vmatrix} $$ \(= \begin{vmatrix} 0 & 0 \\ 0 & 1 \end{vmatrix} \textbf{i} - \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} \textbf{j} + \begin{vmatrix} 1 & 0 \\ 0 & 0 \end{vmatrix} \textbf{k} \) \(= (0-0)\textbf{i} -(1-0)\textbf{j}+(0-0)\textbf{k} \) \(= 0\textbf{i} -1\textbf{j} + 0\textbf{k} \)

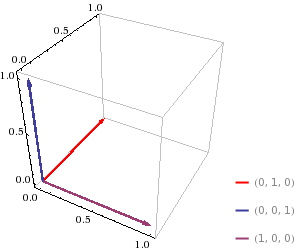Figure 11.4.6

$$ \textbf{6. } \textbf{k} \times \textbf{i} $$ $$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{vmatrix} $$ \(= \begin{vmatrix} 0 & 1 \\ 0 & 0 \end{vmatrix} \textbf{i} - \begin{vmatrix} 0 & 1 \\ 1 & 0 \end{vmatrix} \textbf{j} + \begin{vmatrix} 0 & 0 \\ 1 & 0 \end{vmatrix} \textbf{k} \) \(= (0-0)\textbf{i} -(0-1)\textbf{j}+(0-0)\textbf{k} \) \(= 0\textbf{i} +1\textbf{j} + 0\textbf{k} \)

Exercise 11.4.10 Finding Cross Products

Find
a. \( \textbf{u} \times \textbf{v} \)
b. \( \textbf{v} \times \textbf{u} \)
c. \( \textbf{v} \times \textbf{v} \)

\( \textbf{u} = \langle 3, -2, -2 \rangle \)

\( \textbf{v} = \langle 1, 5, 1 \rangle \)

Solution

$$ \textbf{a. } \textbf{u} \times \textbf{v} $$	$$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 3 & -2 & -2 \\ 1 & 5 & 1 \end{vmatrix} $$
	\(= \begin{vmatrix} -2 & -2 \\ 5 & 1 \end{vmatrix} \textbf{i} - \begin{vmatrix} 3 & -2 \\ 1 & 1 \end{vmatrix} \textbf{j} + \begin{vmatrix} 3 & -2 \\ 1 & 5 \end{vmatrix} \textbf{k} \)
	\(= (-2-(-10))\textbf{i} -(3-(-2))\textbf{j}+(-2-15)\textbf{k} \)
	\(= 8\textbf{i} -5\textbf{j} -17\textbf{k} \)

$$ \textbf{b. } \textbf{v} \times \textbf{u} $$	$$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 1 & 5 & 1 \\ 3 & -2 & -2 \end{vmatrix} $$
	\(= \begin{vmatrix} 5 & 1 \\ -2 & -2 \end{vmatrix} \textbf{i} - \begin{vmatrix} 1 & 1 \\ 3 & -2 \end{vmatrix} \textbf{j} + \begin{vmatrix} 1 & 5 \\ 3 & -2 \end{vmatrix} \textbf{k} \)
	\(= (-10-(-2))\textbf{i} -(-2-3)\textbf{j}+(-2-15)\textbf{k} \)
	\(= -8\textbf{i} +5\textbf{j} - 17\textbf{k} \)

$$ \textbf{c. } \textbf{v} \times \textbf{v} $$	$$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 1 & 5 & 1 \\ 1 & 5 & 1 \end{vmatrix} $$
	\(= \begin{vmatrix} 5 & 1 \\ 5 & 1 \end{vmatrix} \textbf{i} - \begin{vmatrix} 1 & 1 \\ 1 & 1 \end{vmatrix} \textbf{j} + \begin{vmatrix} 1 & 5 \\ 1 & 5 \end{vmatrix} \textbf{k} \)
	\(= (5-5)\textbf{i} -(1-1)\textbf{j}+(5-5)\textbf{k} \)
	\(= 0\textbf{i} +0\textbf{j} + 0\textbf{k} \)

Exercise 11.4.16 Find a Cross Product

Find \( \textbf{u} \times \textbf{v} \) and show that is orthogonal to both \( \textbf{u} \) and \( \textbf{v} \).

\( \textbf{u} = \textbf{i} +6\textbf{j}\)

\( \textbf{v} = -2\textbf{i} +\textbf{j} + \textbf{k} \)

Solution

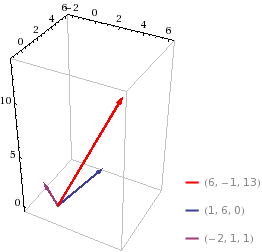Figure 11.4.7

$$ \textbf{u} \times \textbf{v} $$ $$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 1 & 6 & 0 \\ -2 & 1 & 1 \end{vmatrix} $$ \(= \begin{vmatrix} 6 & 0 \\ 1 & 1 \end{vmatrix} \textbf{i} - \begin{vmatrix} 1 & 0 \\ -2 & 1 \end{vmatrix} \textbf{j} + \begin{vmatrix} 1 & 6 \\ -2 & 1 \end{vmatrix} \textbf{k} \) \(= (6-0)\textbf{i} -(1-0)\textbf{j}+(1-(-12))\textbf{k} \) \(= 6\textbf{i} - 1\textbf{j} + 13\textbf{k} \) The vector \( \textbf{u} \times \textbf{v} \) is orthogonal to \( \textbf{u} \) and \( \textbf{v} \) as shown in Figure 11.4.7.

Exercise 11.4.28 Area

Find the area for a triangle with these vertices:

\( A(2,-3,4),\:B(0,1,2),\:C(-1,2,0)\)

Solution
The area for a triangle with \( \textbf{u} \) and \( \textbf{v} \) as adjacent sides is \( 1/2 ( \| \textbf{u} \times \textbf{v} \| ) \).

\(1/2 \| A \times B \| = (-10, -4, 2) = \sqrt{(-10)^{2} + (-4)^{2}+2^{2} } = \sqrt{100+16+4} = \frac{ \sqrt{120}}{2} \)

\(1/2 \| A \times C \| = (-8, -4, 1) = \sqrt{(-8)^{2} + (-4)^{2}+1^{2} } = \sqrt{64+16+1} = \frac{ 9}{2} \)

\(1/2 \| B \times C \| = (-4, -2, 1) = \sqrt{(-4)^{2} + (-2)^{2}+1^{2} } = \sqrt{16+4+1} = \frac{ \sqrt{21}}{2} \)

\(Area = \frac{ \sqrt{120}}{2} + \frac{ 9}{2} + \frac{ \sqrt{21}}{2} \approx 12.241287847 \)

Exercise 11.4.38 Volume

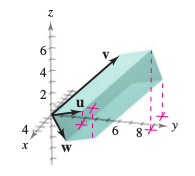Figure 11.4.8

Use the triple scalar product to find the volume of the parallelepiped having adjacent edges \( \textbf{u} \), \( \textbf{v} \) and \( \textbf{w} \). As shown in Figure 11.4.8. \( \textbf{u} = \langle 1, 3, 1 \rangle \) \( \textbf{v} = \langle 0, 6, 6 \rangle \) \( \textbf{w} = \langle -4, 0, -4 \rangle \) $$ V $$ $$= \begin{vmatrix} 1 & 3 & 1 \\ 0 & 6 & 6 \\ -4 & 0 & -4 \end{vmatrix} $$ \(= 1\begin{vmatrix} 6 & 6 \\ 0 & -4 \end{vmatrix} - 3 \begin{vmatrix} 0 & 6 \\ -4 & -4 \end{vmatrix} \textbf{j} + 1\begin{vmatrix} 0 & 6 \\ -4 & 0 \end{vmatrix} \textbf{k} \) \(= 1(-24-0) -3(-24-0)+1(-24-0) \) \(= -24-72 + 24 = 72 \)

Internal Links

Parent Article: Calculus III Advanced (Course)