Calculus III Advanced (Course) (14.07) (Homework)
Contents
Section 14.7 Homework
From Calculus 10e by Larson and Edwards, p. 1025. Exercises 26, 36
Exercise 14.7.26 Using Cylindrical Coordinates
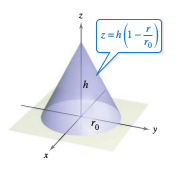
Use cylindrical coordinates to find the cone's volume, as shown in Figure 1.
Solution The mass for the cone is:
| $$\int \int \int_{Q} \: dV $$ | $$= \int \int_{R_{xy}} \int_{0}^{h(1-r/r_{0})} \: dz \: dA$$ |
| $$= \int_{0}^{2 \pi} \int_{0}^{r_{0}} \left(1-\frac{r}{r_{0}} \right)r \: dr \: d\theta$$ | |
| $$= 2 \pi h \left[ \frac{r^{2}}{2} - \frac{r^{3}}{3r_{0}} \right]_{0}^{r_{0}} = \frac{\pi r_{0}^{2}}{3}. $$ |
The \(z\) coordinate has the integral
| $$\int \int \int_{Q} z \: dV$$ | $$=\int \int_{R_{xy}} \int_{0}^{h(1-r/r_{0})} z \: dz \: dA $$ |
| $$= \int_{0}^{2 \pi} \int_{0}^{r_{0}} \frac{1}{2} h^{2} \left(1-\frac{r}{r_{0}} \right)r \: dr \: d\theta $$ | |
| $$=\pi h^{2} \int_{0}^{r_{0}}\left( r-\frac{2r^{2}}{r_{0}}+ \frac{r^{3}}{r_{0}^{2}} \right) \: dr $$ | |
| $$=\pi h^{2} \left[ \frac{r^{2}}{2}- \frac{2r^{3}}{3r_{0}}+ \frac{r^{4}}{4r_{0}^{2}} \right]_{0}^{r_{0}} $$ | |
| $$=\pi h^{2} r_{0}^{2} \left(\frac{1}{2} - \frac{2}{3} + \frac{1}{4} \right) = \frac{\pi h^{2} r_{0}^{2}}{12}. $$ |
Therefore,
- $$\bar{z} = \frac{\int \int \int_{Q} z \: dV}{\int \int \int_{Q} \: dV} = \frac{h}{4}. $$
By symmetry, \(\bar{x} = \bar{y}=0\). Therefore the centroid is: \((\bar{x},\bar{y},\bar{z})=(0,0,h/4).\)
Exercise 14.7.36 Inertia Moment
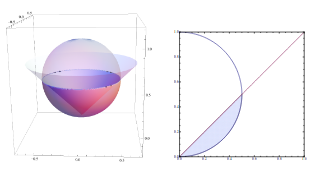
Use cylindrical coordinates to verify the formula for the inertia moment for the solid with uniform density. The solid between the spheres
- \(x^{2}+y^{2}+z^{2}=a^{2}\)
and
- \(x^{2}+y^{2}+z^{2}=b^{2}, \: b > a,\)
and inside the cone
- \(z^{2}=x^{2}+y^{2},\)
as shown in Figure 2.
Solution In spherical coordinates, the equation \(x^{2}+y^{2}+z^{2}=z\) is translated into \( \rho^{2}= \rho \cos \phi \Leftrightarrow \rho = \cos \phi.\) This is a sphere with radius 1/2 centered at \((0,0,1/2).\) The equation \(z^{2}=x^{2}+y^{2}\) is translated to \(\phi = \pi/4\).
| $$\int \int \int_{Q} \: dV $$ | $$= \int_{0}^{2\pi} \int_{\pi/4}^{\pi/2} \int_{0}^{\cos \phi} \rho^{2} \sin \phi \: d\rho \: d\phi \: d\theta $$ |
| $$=2 \pi \int_{\pi/4}^{\pi/2} \sin \phi \frac{\cos^{3} \phi}{3} \: d\phi $$ | |
| $$=\frac{2\pi}{3} \int_{\pi/4}^{\pi/2} \cos^{3} \phi \:d(-\cos \phi) $$ | |
| $$=-\frac{2\pi}{3} \left[ \frac{\cos^{4} \phi}{4} \right]_{\pi/4}^{\pi/2} $$ | |
| $$= \frac{\pi}{6} \left( \frac{1}{\sqrt{2}} \right)^{4}= \frac{\pi}{24}.$$ |
Internal Links
Parent Article: Calculus III Advanced (Course)