Difference between revisions of "Calculus II 09.02 Series and Convergence"
(→Example 9.2.5 Using the Divergence Test for the \(n\)th-Term) |
(No difference)
|
Latest revision as of 23:55, 14 October 2020
| Previous | Calculus II 09.01 Sequences |
| Next | Calculus II 09.03 The Integral Test and p-Series |
Contents
9.2 Series and Convergence
- Understand the definition for a convergent infinite series.
- Use properties of infinite geometric series.
- Use the \(n\)th-Term Test for Divergence for an infinite series.
Infinite Series
If \( \{a_{n}\} \) is an infinite sequence, then
- $$\sum_{n=1}^{\infty}a_{n}= a_{1}+ a_{2}+ a_{3}+ \cdots + a_{n}+ \cdots \color{red}{\text{ Infinite Series}}$$
is an infinite series or simply a series'. The numbers \(a_{1},\:a_{2},\: a_{3} \), and so on are the series' terms. The subscript \(n=x\) denotes on which term the series begins. This is usually 0 or 1. A typesetting convention uses \(\sum a_{n}\) to represent an infinite summation using \(a_{n}\) terms.
To find an infinite series' sum, consider the partial sums sequence listed below.
| \(S_{1}\) | \(= a_{1}\) |
| \(S_{2}\) | \(= a_{1}+a_{2}\) |
| \(S_{3}\) | \(= a_{1}+a_{2}+a_{3}\) |
| \(\vdots\) | |
| \(S_{n}\) | \(= a_{1}+a_{2}+a_{3}+ \cdots+a_{n}\) |
If the partial sums sequence converges, then the series converges and has the sum described in Definition 9.2.1.
Definition 9.2.1 Convergent and Divergent Series
For the infinite series \( \sum_{n=1}^{\infty}a_{n} \), the \(n\)th partial sum is
- $$ S_{n} = a_{1} + a_{2} + a_{3} + \cdots + a_{n}. $$
If the partial sums sequence \( \{ S_{n} \} \) converges to \(S\), then the series converges. The limit \(S\) is called the series sum.
- $$ S = a_{1} + a_{2} + a_{3} + \cdots + a_{n} + \cdots \:\:\:\: \color{red}{S=\sum_{n=1}^{\infty}a_{n} } $$
If \( \{ s_{n} \} \) diverges, then the series diverges.
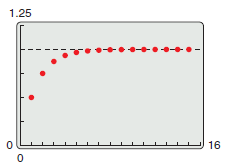
Example 9.2.1 Convergent and Divergent Series
|
|
a. The series
has the partial sums listed below and shown in Figure 9.2.1.
Because
the series converges to 1.
is
Because the limit for \(S_{n}\) is 1, the series converges and its sum is 1.
diverges because \(S_{n}= n\) and the sequence's partial sums diverges. |
Telescoping Series
The series Example 9.2.1(b) is a telescoping series with the form
- $$ (b_{1}-b_{2}) + (b_{2}-b_{3}) + (b_{3}-b_{4}) + \cdots \color{red}{\text{ Telescoping series}} $$
Note that \(b_{2}\) is canceled by the second term, \(b_{3}\) is canceled by the third term, and so on. Because the \(n\)th partial sum is
- $$ S_{n}= b_{1} - b_{n+1} $$
it follows that a telescoping series will converge if and only if \(b_{n}\) approaches a finite number such as \(n \to \infty\). If the series converges, then its sum is
- $$ S_{n}= b_{1} -\lim_{n \to \infty} b_{n+1}. $$
Example 9.2.2 Writing a Series in Telescoping Form
Find the sum for the series
- $$ \sum_{n=1}^{\infty} \frac{2}{4n^{2}-1}$$
Solution Using partial fractions the series can be written as
- $$ a_{n} = \frac{2}{4n^{2}-1} = \frac{2}{(2n-1)(2n+1)}=\frac{1}{2n-1}-\frac{1}{2n+1}.$$
From this telescoping form the \(n\)th partial sum is
- $$ S_{n}= \left ( \frac{1}{1} - \frac{1}{3} \right ) + \left ( \frac{1}{3} - \frac{1}{5} \right ) + \cdots + \left ( \frac{1}{2n-1} - \frac{1}{2n+1} \right ) = 1- \frac{1}{2n+1} . $$
The series converges and its sum is 1. That is,
- $$ \sum_{n=1}^{\infty} \frac{2}{4n^{2}-1} = \lim_{n \to \infty} S_{n} =\lim_{n \to \infty}\left ( 1- \frac{1}{2n+1} \right ) = 1. $$
Geometric Series
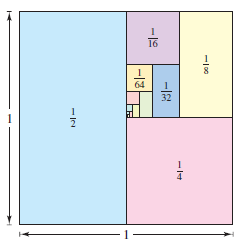
The series in Example 9.2.1(a) is a geometric series. In general, the series
- $$ \sum_{n=1}^{\infty} ar^{n} = a +ar^{1} + ar^{2} + \cdots + ar^{n}+ \cdots, a \ne 0 \color{red}{\text{ Geometric series}} $$
is a geometric series with ratio \(r,\:r \ne 0\).
Theorem 9.2.1 Convergence for a Geometric Series
A geometric series with ratio \(r\) diverges when \(|r| \geqslant 1\). If \(0 < |r| < 1\), then the series converges to the sum
- $$ \sum_{n=0}^{\infty} ar^{n} = \frac{a}{1-r},\:\:\:0<|r|<1 .$$
Proof The series diverges when \(r= \pm 1\). If \(r \ne \pm 1\), then
- $$ S_{n} = a +ar^{1} + ar^{2} + \cdots + ar^{n-1}. $$
Multiplication by \(r\) yields
- $$ rS_{n} = ar +ar^{2} + ar^{3} + \cdots + ar^{n}. $$
Subtracting the second equation from the first produces \(S_{n} - rS_{n} = a - ar^{n}\). Therefore \(S_{n}(1-r)=a(1-r^{n})\), and the \(n\)th partial sum is
- $$ S_{n} = \frac{a}{1-r}(1-r^{n}). $$
When \(0 < |r| < 1\), it follows that \(r^{n} \to 0\) as \(n \to \infty\), and you obtain
- $$ \lim_{n \to \infty} S_{n} = \lim_{n \to \infty} \left [ \frac{a}{1-r}(1-r^{n}) \right ] = \frac{a}{1-r} \left [ \lim_{n \to \infty} (1-r^{n}) \right ] = \frac{a}{1-r} $$
which means the series converges and its sum is \(a/(1-r)\). Showing the series diverges when \(|r| > 1\) is left for later.
Example 9.2.3 Convergent and Divergent Geometric Series
a. The geometric series
- $$ \sum_{n=0}^{\infty} \frac{3}{2^{n}} = \sum_{n=0}^{\infty}3 \left ( \frac{1}{2} \right )^{n} = 1 + \frac{3}{2} + \frac{9}{4} + \frac{27}{8} + \cdots$$
has the ratio \(r=1/2\) with \(a=3\). Because \(0 < |r| < 1\), the series converges and its sum is
- $$ S=\frac{a}{1-r}=\frac{3}{1-(1/2)}=6. $$
b. The geometric series
- $$ \sum_{n=0}^{\infty} \left ( \frac{3}{2} \right )^{n} = 1 + \frac{3}{2} + \frac{9}{4} + \cdots$$
has the ratio \(r=3/2\). Because \( |r| \geqslant 1\), the series diverges.
Example 9.2.4 A Geometric Series for a Repeating Decimal
Us a geometric series to write \(0.\overline{08}\) as a ratio with two integers.
Solution The repeating decimal \(0.\overline{08}\) can be written as
| $$ 0.080808 \cdots$$ | $$ = \frac{8}{10^{2}} +\frac{8}{10^{4}} +\frac{8}{10^{6}} + \cdots $$ |
| $$ \sum_{n=0}^{\infty} \left ( \frac{8}{10^{2}} \right ) \left ( \frac{1}{10^{2}} \right )^{n}. $$ |
For this series \(a=8/10^{2}\) and \(r=1/10^{2}\). This produces
- $$ 0.080808 \cdots = \frac{a}{1-r} = \frac{8/10^{2}}{1-(1/10^{2})} = \frac{8}{99} $$
To verify divide 8 by 99 on a calculator to see if it produces \(0.\overline{08}\).
A series convergence is not affected by removing a fixed number of terms from the series beginning. For example, The geometric series
- $$ \sum_{n=4}^{\infty} \left ( \frac{1}{2} \right )^{n} \text{ and } \sum_{n=0}^{\infty} \left ( \frac{1}{2} \right )^{n} $$
both converge. Because the sum for the second series is
- $$ S=\frac{a}{1-r}=\frac{1}{1-(1/2)}=2 $$
means the sum for the first series is
- $$ S =2 - \left [ \left ( \frac{1}{2} \right )^{0} + \left ( \frac{1}{2} \right )^{1} + \left ( \frac{1}{2} \right )^{2} + \left ( \frac{1}{2} \right )^{3} \right ] = 2 - \frac{15}{8} = \frac{1}{8}$$
Theorem 9.2.2 Infinite Series Properties
Let \( \sum a_{n} \) and \( \sum b_{n} \) be convergent series, and let \(A\), \(B\), and \(c\) be real numbers. If \( \sum a_{n} = A \) and \( \sum b_{n}=B \), then the following series converge to the following sums.
- $$1. \: \sum_{n=1}^{\infty} ca_{n} = cA $$
- $$2. \: \sum_{n=1}^{\infty} (a_{n} + b_{n}) = A+B $$
- $$3. \: \sum_{n=1}^{\infty} (a_{n} - b_{n}) = A-B $$
Divergence Test for the \(n\)th-Term
The next theorem states that wen a series converges the limit for its \(n\)th term must be 0.
Theorem 9.2.3 Limit for the \(n\)th Term in a Convergent Series
- $$\text{If } \sum_{n=1}^{\infty} a_{n} \text{ converges, then } \lim_{n \to \infty} a_{n} = 0. $$
Proof Assume that
- $$ \sum_{n=1}^{\infty} a_{n} = \lim_{n \to \infty} S_{n} = L.$$
Because \(S_{n} = S_{n-1} + a_{n}\) and
- $$ \lim_{n \to \infty} S_{n} = \lim_{n \to \infty} S_{n-1} = L$$
it follows that
- $$L = \lim_{n \to \infty} S_{n} $$
- $$ = \lim_{n \to \infty} ( S_{n-1} + a_{n} ) $$
- $$ = \lim_{n \to \infty} S_{n-1} + \lim_{n \to \infty} a_{n} $$
- $$ = L + \lim_{n \to \infty} a_{n} $$
which implies that \( \{a_{n}\} \) converges to 0.
Theorem 9.2.4 Divergence Test for the \(n\)th-Term
The contrapositive for Theorem 9.2.3 provides a useful test for divergence. This \(n\)th-Term Test for Divergence states that if the limit for the \(n\)th term in a series does not converge to 0, then the series must diverge. Formally this is described as
- $$\text{If } \sum_{n=1}^{\infty} a_{n} \ne 0, \text{ then } \sum_{n=1}^{ \infty} a_{n} \text{ diverges.} $$
Example 9.2.5 Using the Divergence Test for the \(n\)th-Term
a. For the series
- $$ \sum_{n=0}^{\infty} 2_{n} $$
you have
- $$ \lim_{n \to \infty} 2_{n} = \infty. $$
therefore the limit for the \(n\)th term is not 0 and the series diverges.
b. For the series
- $$ \sum_{n=0}^{\infty} \frac{n!}{2n! + 1} $$
you have
- $$ \lim_{n \to \infty} \frac{n!}{2n! + 1} = \frac{1}{2}. $$
therefore the limit for the \(n\)th term is not 0 and the series diverges.
c. For the series
- $$ \sum_{n=0}^{\infty} \frac{1}{n} $$
you have
- $$ \lim_{n \to \infty} \frac{1}{n} = 0. $$
Because the limit for the \(n\)th term is 0, the \(n\)th-Term Test for Divergence does not apply and no conclusions can be drawn about convergence or divergence. Section 9.3 will show that this particular series diverges.
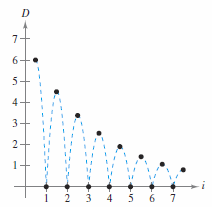
Example 9.2.6 The Bouncing Ball Problem
|
A rubber ball is dropped from 6 feet onto a hard, smooth floor, and begins bouncing, as shown in Figure 9.2.3. The each bounce has a height that is three-fourths the height for the previous bounce. Find the total vertical distance traveled by the ball. In computer graphics the bouncing ball problem is a popular exercise.
and
By continuing this process the bouncing becomes a convergent series with the total distance
|
Internal Links
Parent Article: Calculus II 09 Infinite Series