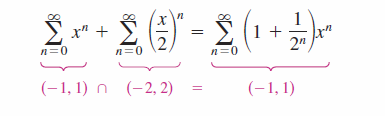Calculus II 09.09 Using Power Series to Represent a Function
| Previous | Calculus II 09.08 Power Series |
| Next | Calculus II 10 Conics Parametric Equations and Polar Coordinates |
Contents
9.9 Using Power Series to Represent a Function
- Find a geometric power series that represents a function.
- Construct a power series using series operations.
Geometric Power Series[1]
|
|
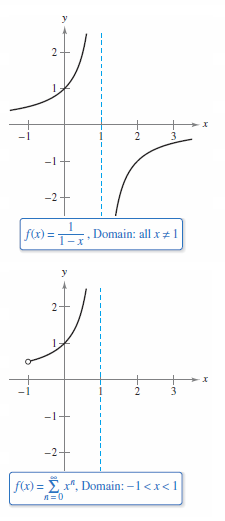
A Power Series can represent some function \(f(x)\), but only over a single interval. Consider the function
This form for \(f\) closely resembles the sum for a geometric series
In other words, when \(a=1\) and \(r=x\), a power series representation for \(f\) centered at 0 looks like
This series represents \(f\) only on the interval (-1,1), whereas \(f\) is defined for all \(x \ne 1\), as shown in Figure 9.9.1. To represent \(f\) on another interval, a different series is needed. For instance, the power series centered at -1 could be written as
which implies that \(a=1/2\) and \(r=(x+1)/2\). Taking \(|x+1|<2\) yields
which converges on the interval (-3,1). |
Example 9.9.1 Finding a Geometric Power Series Centered at Zero
Find a power series for
- $$ f(x)=\frac{4}{x+2}$$
centered at 0.
Solution Writing \(f(x)\) as \(a/(1-r)\) produces
- $$ \frac{4}{x+2} = \frac{2}{1-(-x/2)} = \frac{a}{1-r}$$
which implies that \(a=2\) and
- $$r=-\frac{x}{2}. $$
The power series for \(f\) is
| $$ \frac{4}{x+2} $$ | $$= \sum_{n=0}^{\infty} ar^{n}$$ |
| $$= \sum_{n=0}^{\infty} 2 \left( - \frac{x}{2} \right)^{n} $$ | |
| $$= 2 \left( 1 - \frac{x}{2} + \frac{x^{2}}{4} - \frac{x^{3}}{8} \right). $$ |
The power series converges when
- $$\left | -\frac{x}{2} \right | < 1 $$
which produces a convergence interval at (-2,2).
Operations with Power Series
- $$\text{Let }f(x)= \sum_{n=0}^{\infty} a_{n}x^{n} \text{ and } g(x)= \sum_{n=0}^{\infty} b_{n}x^{n}.$$
- $$1.\:f(kx)= \sum_{n=0}^{\infty} a_{n}k^{n}x^{n} $$
- $$2.\:f(x^{N})= \sum_{n=0}^{\infty} a_{n}x^{nN} $$
- $$3.\:f(x)\pm g(x)= \sum_{n=0}^{\infty} (a_{n} \pm b_{n})x^{n} $$
The operations can change the convergence interval for the resulting series. For example, in the addition shown below, the convergence interval for the sum is the intersection between the two original series' convergence intervals. As shown in Figure 9.9.2 below.
Example 9.9.2 Adding Two Power Series
Find a power series for
- $$ f(x)=\frac{3x-1}{x^{2}-1}$$
centered at 0.
Solution Using partial fractions \(f\) can be written as
- $$ \frac{3x-1}{x^{2}-1} = \frac{2}{x+1} + \frac{1}{x-1}.$$
By adding the two geometric power series
- $$ \frac{2}{x+1} = \frac{2}{1-(-x)} = \sum_{n=0}^{\infty} 2(-1)^{n}x^{n}, \: |x| < 1 $$
and
- $$ \frac{1}{x-1} = \frac{-1}{1-x} = - \sum_{n=0}^{\infty} x^{n}, \: |x| < 1 $$
produces the power series below
| $$ \frac{3x-1}{x^{2}-1} $$ | $$= \sum_{n=0}^{\infty} [2(-1)^{n}-1]x^{n}$$ |
| $$= 1-3x+x^{2} - 3x^{3}+ x^{4}- \cdots $$ |
The convergence interval for the added power series is (-1,1).
Example 9.9.3 Adding Two Power Series
Find a power series for
- $$ f(x)=\ln x$$
centered at 1.
Solution A power series centered at 1 produces
- $$ \frac{1}{x} = \sum_{n=0}^{\infty} (-1)^{n}(x-1)^{n} \:\:\:\: \color{red}{\text{Convergence interval = (0,2) }}.$$
Integrating this series produces
| $$ \ln x $$ | $$= \int \frac{1}{x}dx+C$$ |
| $$= C+\sum_{n=0}^{\infty} (-1)^{n} \frac{(x-1)^{n-1}}{n+1}.$$ |
By letting \(x=1\), yields \(C=0\). Therefore,
| $$ \ln x $$ | $$= \int \frac{1}{x}dx+C$$ |
| $$= \frac{(x-1)}{1} - \frac{(x-1)^{2}}{2} + \frac{(x-1)^{3}}{3}-\frac{(x-1)^{4}}{4}+\cdots \:\:\:\: \color{red}{\text{Convergence interval = (0,2] }}$$ |
Note that the series converges at \(x=2\). This is consistent with the observation in Section 9.8 that power series integration may alter the convergence at the interval endpoints.
Example 9.9.4 Finding a Power Series by Integration
Find a power series for
- $$ g(x)=\arctan x$$
centered at 0.
Solution Because
- $$ D_{x}[\arctan x]=\frac{1}{(1+x^{2})}$$
the series below can be used.
- $$ f(x) = \frac{1}{1+x} = \sum_{n=0}^{\infty} (-1)^{n}x^{n} \:\:\:\: \color{red}{\text{Convergence interval = (-1,1) }}$$
Substituting \(x^{2}\) for \(x\) produces
- $$ f(\color{red}{x^{2}}) = \frac{1}{1+\color{red}{x^{2}}} = \sum_{n=0}^{\infty} (-1)^{n}x^{2n}. $$
Integrating yields
| $$ \arctan x $$ | $$= \int \frac{1}{1+x^{2}}dx+C$$ |
| $$= C+\sum_{n=0}^{\infty} (-1)^{n} \frac{x^{2n+1}}{2n+1}.$$ | |
| $$= \sum_{n=0}^{\infty} (-1)^{n} \frac{x^{2n+1}}{2n+1} \:\:\:\: \color{red}{\text{Let }x=0\text{, then }C=0}$$ | |
| $$= x - \frac{x^{3}}{3} + \frac{x^{5}}{5}- \frac{x^{7}}{7}+ \:\:\:\: \color{red}{\text{Convergence interval = (-1,1) }}$$ |
Example 9.9.5 Approximating \(\pi\) with Two Series
Use the trigonometric identity
- $$ 4 \arctan \frac{1}{5} - \arctan \frac{1}{239} = \frac{\pi}{4} $$
to approximate the number \(\pi\).
Solution Using the first five terms from each series yields
- $$ 4 \left ( 4 \arctan \frac{1}{5} - \arctan \frac{1}{239} \right ) \approx 3.1415926 $$
which agrees with the exact value for \(\pi\) with an error less than 0.0000001.
Internal Links
Parent Article: Calculus II 09 Infinite Series