Calculus III 15.01 Vector Fields

Previous	Calculus III 14 Multiple Integration
Next	Calculus III 15.02 Line Integrals

15.1 Vector Fields

• Understand the vector field concept.
• Determine whether a vector field is conservative.
• Find the curl for a vector field.
• Find the divergence for a vector field.

Vector Fields

Chapter 12 described vector-valued functions as functions that assign a vector to a real number and how they can describe curves and motions along a curve. Chapter 15 extends that discussion to two new vector-valued functions, functions that assign a vector to a point in the plane or a point in three dimensions. These fields are called vector fields and are used to describe various force fields and velocity fields.

Definition 15.1.1 Vector Field

Rotating wheel Figure 15.1.1 Air flow vector field Figure 15.1.2 Gravitational force field Figure 15.1.3

A vector field over a plane region \(R\) is a function \(\textbf{F}\) that assigns a vector \(\textbf{F}(x,y)\) to each point in \(R\). A vector field over a solid region \(Q\) in three dimensions is a function \(\textbf{F}\) that assigns a vector \(\textbf{F}(x,y,z)\) to each point in \(Q\). Although any region has infinitely many points, and thus infinitely many vectors, a good description for the field can be expressed by choosing a representative point subset with vectors \(\textbf{F}(x,y)\) whose initial points are \((x,y)\). The gradient is a vector field type. Consider \(f(x,y)=x^{2}y+3xy^{3}\) then the gradient for \(f\) \( \nabla f(x,y) \) \(= f_{x}(x,y)\textbf{i} +f_{y}(x,y)\textbf{j} \) \(= (2xy + 3y^{3})\textbf{i} + (x^{2} + 9xy^{2})\textbf{j} \: \: \: \: \)     Vector field in the plane is a vector field in the plane. Chapter 13 described a graphical interpretation for this field as a vector family, where each points toward the maximum increase along the surface given by \(z=f(x,y)\). In three dimensions, if \(f(x,y,z) = x^{2} + y^{2} + z^{2}\) then the gradient for \(f\) \( \nabla f(x,y,z) \) \(= f_{x}(x,y,z)\textbf{i} +f_{y}(x,y,z)\textbf{j} +f_{z}(x,y,z)\textbf{k} \) \(= 2x\textbf{i} + y^{2}\textbf{j} + z^{2}\textbf{k} \: \: \: \: \)      Vector field in the three dimensions is a vector field in three dimensions. Note the component functions for this vector field are \(2x\), \(2y\), and \(2z\). A vector field \(\textbf{F}(x,y,z) = M(x,y,z)\textbf{i} + N(x,y,z)\textbf{j} + P(x,y,z)\textbf{k} \) is continuous at a point if and only if each component function, \(M\), \(N\), and \(P\) is continuous at that point. Some common physical examples for vector fields are velocity fields, gravitational fields, and electric force fields. 1. Velocity fields describe how particles move as a group in the plane or in three dimensions. For instance, Figure 15.1.1 shows the vector field determined by a wheel rotating on an axle. Notice the longer vectors are farther from the axle. Velocity fields are also determined by the liquids flowing through a container or by the air flow currents around a moving object, as shown in Figure 15.1.2. 2. Gravitational fields are defined by Newton’s Law of Gravitation[1], which states that the attraction force exerted on a particle with mass \(m_{1}\) located at \((x,y,z)\) by a particle with mass \(m_{2}\) located at \((0,0,0)\) is $$\textbf{F}(x,y,z) = \frac{-Gm_{1}m_{2}}{x^{2} + y^{2} + z^{2}}\textbf{u} $$ where \(G\) is the gravitational constant and \(\textbf{u}\) is the unit vector in the direction from the origin to \((x,y,z)\). The gravitational field \(\textbf{F}\) has the properties that \(\textbf{F}(x,y,z)\) always points toward the origin, and that its magnitude is the same at all points equidistant from the origin, as shown in Figure 15.1.3. A vector field with these two properties is called a central force field. Using the position vector \(\textbf{r}= x\textbf{i}+y\textbf{j}+z\textbf{k}\) for point \((x,y,z)\), the gravitational field \(\textbf{F}\) can be written as $$\textbf{F}(x,y,z) = \frac{-Gm_{1}m_{2}}{\|\textbf{r}\|^{2}} \left( \frac{\textbf{r}}{\|\textbf{r}\|} \right)\textbf{r}= \frac{-Gm_{1}m_{2}}{\|\textbf{r}\|^{2}} \textbf{u}.$$ 3. Electric force fields are defined by Coulomb's Law[2], which states that the force exerted on a particle with electric charge \(q_{1}\) located at \((x,y,z)\) by a particle with electric charge \(q_{2}\) located at \((0,0,0)\) is $$\textbf{F}(x,y,z) = \frac{c \:q_{1}q_{2}}{\|\textbf{r}\|^{2}} \textbf{u}$$ where \(\textbf{r}= x\textbf{i}+y\textbf{j}+z\textbf{k}\), \( \textbf{u} = \textbf{r}/ \|\textbf{r}\|\), and \(c\) is a constant that depends on the units chosen for \(\|\textbf{r}\|\), \(q_{1}\) and \(q_{2}\). Note thr electric force field has the same form as a gravitational field. Such a field is called an inverse square field, as described in Definition 15.1.2.

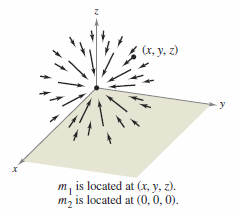
Definition 15.1.2 Inverse Square Field

Let \(\textbf{r}(t) = x(t)\textbf{i}+y(t)\textbf{j}+ z(t)\textbf{k}\) be a position vector The vector field \(\textbf{F}\) is an inverse square field if

$$\textbf{F}(x,y,z) = \frac{k}{\|\textbf{r}\|^{2}} \textbf{u}$$

where \(k\) is a real number and

$$\textbf{u}= \frac{\textbf{r}}{\|\textbf{r}\|} $$

is a unit vector in \(\textbf{r}\)'s direction.

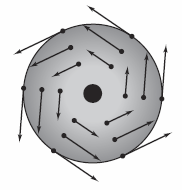
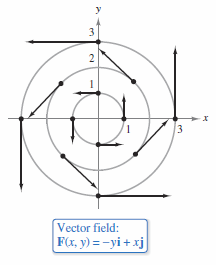
Example 15.1.1 Sketching a Vector Field on a Circle

Figure 15.1.4

Sketch some vectors in the vector field \(\textbf{F}(x,y)= -y\textbf{i}+x\textbf{j}. \) Solution Because any vector field has infinitely many vectors, it is not possible to create a sketch that covers the entire field. Instead, enough vectors will be sketched to visualize the field by plotting vectors in groups with equal magnitude. This corresponds to finding level curves in scalar fields. Here, vectors with equal magnitude lie on circles. \(\| \textbf{F}\| \) \(=c \)     Vectors with length \(c\) \(\sqrt{x^{2}+y^{2}}\) \(=c \) \(x^{2}+y^{2}\) \(=c^{2} \)     Equation for a circle Choose a value for \(c\) and plot several vectors on the resulting circle. The following vectors occur on the unit circle, as shown in Figure 15.1.4. Point Vector \((1,0)\) \(\textbf{F}(1,0)= \textbf{j}\) \((0,1)\) \(\textbf{F}(0,1)= -\textbf{i}\) \((-1,0)\) \(\textbf{F}(-1,0)= -\textbf{j} \) \((0,-1) \:\:\:\: \) \(\textbf{F}(0,-1)= \textbf{i} \) Note in the figure that this vector field is similar to that given by the rotating wheel shown in Figure 15.1.1.

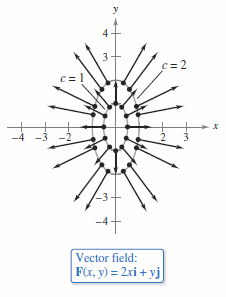
Example 15.1.2 Sketching a Vector Field on an Ellipse

Figure 15.1.5

Sketch some vectors in the vector field \(\textbf{F}(x,y)= 2x\textbf{i}+y\textbf{j}. \) Solution Vectors with equal length lie on ellipses given by \( \| \textbf{F} \| \) \(=c \) \(\sqrt{ (2x)^{2} +(y)^{2}} \) \(=c \) which implies that \( 4x^{2}+y^{2} = c^{2}. \)     Ellipse equation For \(c=1\), sketch several vectors \(2x\textbf{i}+y\textbf{j}\) with magnitude 1 at points on the ellipse given by \( 4x^{2}+y^{2} =1,\) as shown on the inner ring in Figure 15.1.5. For \(c=2\), sketch several vectors \(2x\textbf{i}+y\textbf{j}\) with magnitude 2 at points on the ellipse given by \( 4x^{2}+y^{2} = 4,\) as shown on the inner ring in Figure 15.1.5.

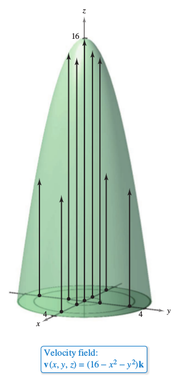
Example 15.1.3 Sketching a Velocity Field

Figure 15.1.6

Sketch some vectors in the velocity field \(\textbf{v}(x,y,z) = (16-x^{2}-y^{2})\textbf{k} \) where \(x^{2}+y^{2} \leqslant 16.\) Solution The function \(\textbf{v}\) describes the velocity for a liquid flowing through a tube with radius four. Vectors near the \(z\)-axis are longer than those near the tube wall. For example, at the point \((0,0,0)\), the velocity is \(\textbf{v}(0,0,0) = 16\textbf{k} \), whereas at the point \((0,3,0)\), the velocity is \(\textbf{v}(0,3,0) = 7\textbf{k},\) as shown in Figure 15.1.6. Thus, the liquid flows faster at the tube's center than at the edge.

Conservative Vector Fields[3]

Notice in Figure 15.1.5 that all the vectors appear to be normal to the level curve from which they emanate. Because this is a gradient property, it is natural to ask whether the vector field

\(\textbf{F}(x,y)= 2x\textbf{i}+y\textbf{j} \)

is the gradient for some differentiable function \(f\). The answer is that some vector fields can be represented as the gradients for differentiable functions and some cannot — those that can are called conservative vector fields.

Definition 15.1.3 Conservative Vector Field

A vector field \(F\) is called conservative when there exists a differentiable function \(f\) such that \(F=\nabla f.\) The function \(f\) is called the potential function for \(F\).

Example 15.1.4 Conservative Vector Fields

a.

Prove the vector field described by \(\textbf{F}(x,y)=2x\textbf{i}+y\textbf{j} \) is conservative. Consider the potential function \(f(x,y)=x^{2}+\frac{1}{2}y^{2}\). Because \(\nabla f= 2x\textbf{i}+y\textbf{j} = \textbf{F}\) if follows that \(\textbf{F}\) is conservative.

b.

Prove that every inverse square field is conservative. Let $$ \textbf{F}(x,y,z) = \frac{k}{\|\textbf{r}\|^{2}}\textbf{u} \text{ and } f(x,y,z) = \frac{-k}{\sqrt{x^{2} + y^{2} + z^{2}}}$$ where \(\textbf{u} = \textbf{r}/ \| \textbf{r}\| \). Because \(\nabla f\) $$= \frac{kx}{(x^{2} + y^{2} + z^{2})^{3/2}}\textbf{i} + \frac{ky}{(x^{2} + y^{2} + z^{2})^{3/2}}\textbf{j} + \frac{kz}{(x^{2} + y^{2} + z^{2})^{3/2}}\textbf{k} $$ $$=\frac{k}{x^{2} + y^{2} + z^{2}} \left( \frac{x\textbf{i}+y\textbf{j}+z\textbf{k}}{\sqrt{x^{2} + y^{2} + z^{2}}} \right) $$ $$= \frac{k}{\|\textbf{r}\|^{2}} \frac{\textbf{r}}{\|\textbf{r}\|} = \frac{k}{\|\textbf{r}\|^{2}}\textbf{u}$$ it follows that \(\textbf{F}\) is conservative.

As illustrated in Example 15.1.4(b), many important vector fields, including gravitational fields and electric force fields, are conservative. This terminology comes from physics. For example, the term “conservative” is derived from the classic physical law regarding the conservation of energy. This law states that the sum of the kinetic energy and the potential energy for a particle moving in a conservative force field is constant. (The kinetic energy of a particle is the energy due to its motion, and the potential energy is the energy due to its position in the force field.) Theorem 15.1.1 describes the necessary and sufficient conditions for a conservative vector field in the plane.

Theorem 15.1.1 Test for Conservative Vector Field in the Plane

Let \(M\) and \(N\) have continuous first partial derivatives on an open disk \(R\). The vector field \(\textbf{F}(x,y)= M \textbf{i} + N\textbf{j}\) is conservative if and only if

$$ \frac{\partial N}{\partial x} = \frac{\partial M}{\partial y}.$$

Proof To prove the given condition is necessary for \(\textbf{F}\) to be conservative, suppose there exists a potential function \(f\) such that

\(\textbf{F}(x,y)= \nabla f(x,y)= M \textbf{i} + N\textbf{j}.\)

This produces

$$f_{x}(x,y) $$	$$=M $$	\(\rightarrow\)	$$f_{xy}(x,y)= \frac{\partial M}{\partial y} $$
$$f_{y}(x,y) $$	$$=N $$	\(\rightarrow\)	$$f_{yx}(x,y)= \frac{\partial N}{\partial x} $$

and, by the equivalence between the mixed partials \(f_{xy}\) and \(f_{yx}\) the conclusion is that

$$ \frac{\partial N}{\partial x} = \frac{\partial M}{\partial y} $$

for all \((x,y)\) in \(R\). This condition is proved in more detail in Section 15.4.

Finding a potential function for \(\textbf{F}\) is comparable to antidifferentiation. Sometimes it can be found through inspection. As described in Example 15.1.4.

Example 15.1.5 Testing for Conservative Vector Fields in the Plane

Determine if the vector field given by \(\textbf{F}\) is conservative.

\(\textbf{a. } \: \textbf{F}(x,y) = x^{2}y\textbf{i} + xy\textbf{j} \:\:\:\: \textbf{b. }\: \textbf{F}(x,y) = 2x\textbf{i} + y\textbf{j}\)

Solution

a.	The vector field \(\textbf{F}(x,y) = x^{2}y\textbf{i} + xy\textbf{j}\) is not conservative because $$ \frac{\partial M}{\partial y} = \frac{\partial}{\partial y}[x^{2}y]=x^{2} \text{ and } \frac{\partial N}{\partial x} = \frac{\partial}{\partial x}[xy]=y.$$
b.	The vector field \(\textbf{F}(x,y) = 2x\textbf{i} + y\textbf{j} \) is conservative because $$ \frac{\partial M}{\partial y} = \frac{\partial}{\partial y}[2x]=0 \text{ and } \frac{\partial N}{\partial x} = \frac{\partial}{\partial x}[y]=0.$$

Example 15.1.6 Finding a Potential Function for \(\textbf{F}(x,y)\)

Find a potential function for

\(\textbf{F}(x,y) = 2xy\textbf{i} + (x^{2}-y)\textbf{j}.\)

Solution Applying Theorem 15.1.1 it follows that \(\textbf{F}\) is conservative because

$$ \frac{\partial }{\partial y}[2xy]=2x \text{ and } \frac{\partial }{\partial x}[x^{2}-y]=2x. $$

If \(f\) is a function whose gradient is equal to \(\textbf{F}(x,y)\), then

\(\nabla f(x,y) = 2xy\textbf{i} +(x^{2}-y)\textbf{j}\)

which implies that

\(f_{x}(x,y)=2xy\)

and

\(f_{y}(x,y)=x^{2}-y.\)

To reconstruct the function \(f\) from these two partial derivatives, integrate \(f_{x}(x,y)\) with respect to \(x\)

$$f(x,y)= \int f_{x}(x,y) \: dx = \int 2xy \: dx = x^{2}y+g(y) $$

and integrate \(f_{y}(x,y)\) with respect to \(y\)

$$f(x,y)= \int f_{y}(x,y) \: dy = \int (x^{2}-y) \: dy = x^{2}y - \frac{y^{2}}{2}+h(x). $$

Notice that \(g(y)\) is constant with respect to \(x\) and \(h(x)\) is constant with respect to \(y\). To find a single expression that represents \(f(x,y)\), let

$$ g(y) = - \frac{y^{2}}{2} \text{ and } h(x) = K.$$

Then the function can be written as

\(f(x,y)\)	\(= x^{2}y+g(y) + K\)
	\(= x^{2}y+g(y) - \frac{y^{2}}{2} + K. \)

The result can be checked by forming the gradient for \(f\) and finding it equal to the original function \(\textbf{F}\).

Notice that the solution is comparable to an indefinite integral. In that, the solution represents a set with potential functions where any two differ by a constant. Finding a unique solution requires an initial condition that is satisfied by the potential function.

Curl for a Vector Field

Definition 15.1.4 Curl for a Vector Field

The curl for \(\textbf{F}(x,y,z) = M \textbf{i}+N\textbf{j}+P\textbf{k}\) is

curl \(\textbf{F}(x,y,z)\)	\(= \nabla \times \textbf{F}(x,y,z) \)
	$$= \left( \frac{\partial P}{\partial y} - \frac{\partial N}{\partial z} \right) \textbf{i} - \left( \frac{\partial P}{\partial x} - \frac{\partial M}{\partial z} \right) \textbf{j}+\left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} \right) \textbf{k} $$

if curl \(\textbf{F}=\textbf{0}\), then \(\textbf{F}\) is irrotational[4].

The cross product notation used for curl comes from viewing the gradient \(\nabla f\) as resulting from the differential operator \(\nabla\) acting on the function \(f\). This context is useful in remembering the curl formula in a determinant form, as shown in the following formula.

curl \(\textbf{F}(x,y,z)\)	\(=\nabla \times \textbf{F}(x,y,z)\)
	$$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\ M & N & P \end{vmatrix}$$
	$$= \left( \frac{\partial P}{\partial y} - \frac{\partial N}{\partial z} \right) \textbf{i} - \left( \frac{\partial P}{\partial x} - \frac{\partial M}{\partial z} \right) \textbf{j}+\left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} \right) \textbf{k}$$

Example 15.1.7 Finding the Curl for a Vector Field

Find curl \(\textbf{F}\) for the vector field

\(\textbf{F}(x,y,z)= 2xy\textbf{i} + (x^{2}+z^{2})\textbf{j} + 2yz\textbf{k},\)

and determine if \(\textbf{F}\) is irrotational.
Solution The curl for \(\textbf{F}\) is

curl \(\textbf{F}(x,y,z)\)	\(=\nabla \times \textbf{F}(x,y,z)\)
	$$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\ 2xy & x^{2}+y^{2} & 2yz \end{vmatrix}$$
	$$= \begin{vmatrix} \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\ x^{2}+y^{2} & 2yz\end{vmatrix} \textbf{i}-\begin{vmatrix} \frac{\partial }{\partial x} & \frac{\partial }{\partial z}\\ 2xy & 2yz\end{vmatrix} \textbf{j}+\begin{vmatrix} \frac{\partial }{\partial x} & \frac{\partial }{\partial y}\\ 2xy & x^{2}+y^{2}\end{vmatrix} \textbf{k}$$
	\(= (2z-2z)\textbf{i}-(0-0)\textbf{j}+(2x-2x)\textbf{k} = \textbf{0} \)

Because curl \(\textbf{F} = \textbf{0}\), \(\textbf{F}\) is irrotational and conservative.

Theorem 15.1.2 Test for Conservative Vector Field in Three Dimensions

Suppose that \(M\), \(N\), and \(P\) have continuous first partial derivatives in an open sphere \(Q\) in three dimensions. The vector field

\(\textbf{F}(x,y,z)= M\textbf{i} + N\textbf{j} + P\textbf{k}\)

is conservative if and only if

curl \( \textbf{F}(x,y,z)= \textbf{0}.\)

That is, \( \textbf{F}\) is conservative if and only if

$$ \frac{\partial P}{\partial y} = \frac{\partial N }{\partial z}, \: \frac{\partial P}{\partial x} = \frac{\partial M }{\partial z} \text{, and }\frac{\partial N}{\partial x} = \frac{\partial M}{\partial y}.$$

This theorem is valid for simply connected domains in three dimensions. A simply connected domain in three dimensions is a domain \(D\) for which every simple closed curve in \(D\) can be shrunk to a point in \(D\) without leaving \(D\). This is described in greater detail in Section 15.4.

Example 15.1.8 Finding a Potential Function for \( \textbf{F}(x,y,z)\)

Find a potential function for

\( \textbf{F}(x,y,z) = 2xy\textbf{i} + (x^{2}+z^{2})\textbf{j} + 2yz \textbf{k}.\)

Solution Example 15.1.7 proved the vector field given by \( \textbf{F}\) is conservative. If \(f\) is a function such that \( \textbf{F}(x,y,z) = \nabla f(x,y,z)\), then

\(f_{x}(x,y,z)=2xy, \: f_{y}(x,y,z) = x^{2}+z^{2} \text{, and } f_{z}(x,y,z)=2yz \)

and integrating with respect to \(x\), \(y\), and \(z\) separately produces

$$f(x,y,z) $$	$$=\int M \: dx $$	$$= \int 2xy \: dx $$	$$= x^{2}y+g(y,z) $$
$$f(x,y,z) $$	$$=\int N \: dy $$	$$= \int (x^{2}+z^{2}) \: dy $$	$$=x^{2}y+yz^{2} +h(x,z) $$
$$f(x,y,z) $$	$$=\int P \: dz $$	$$=\int 2yz \: dz $$	$$= yz^{2} + k(x,y). $$

Comparing the three partial integration versions for \(f(x,y,z)\) produces

\(g(y,z) = yz^{2} + K, \: h(x,z)=K \text{, and }k(x,y) = x^{2}y+K.\)

Therefore, \(f(x,y,z)\) is given by

\(f_{x}(x,y,z)=x^{2}y+yz^{2}+K.\)

Examples 15.1.6 and 15.1.8 illustrate a problem called recovering a function from its gradient. One solution uses successive “partial integrations” and partial differentiations to find a potential function. Differential Equations has other solutions for this problem.

Divergence for a Vector Field

The curl for a vector field \(\textbf{F}\) is itself a vector field. Another important function defined on a vector field is divergence, which is a scalar function.

Definition 15.1.5 Divergence for a Vector Field

The divergence for \(\textbf{F}(x,y)=M \text{i}+N\text{j}\) is
$$ \text{div }\textbf{F}(x,y) = \nabla \cdot \textbf{F}(x,y) = \frac{\partial M}{\partial x} + \frac{\partial N}{\partial y}.$$	Plane
The divergence for \(\textbf{F}(x,y,z)=M \text{i}+N\text{j}+P\text{k}\) is
$$ \text{div }\textbf{F}(x,y,z) = \nabla \cdot \textbf{F}(x,y,z) = \frac{\partial M}{\partial x} + \frac{\partial N}{\partial y} + \frac{\partial P}{\partial z}.$$	Three dimensions

If div \(\textbf{F}=\textbf{0}\), then \(\textbf{F}\) is divergence free.

The dot product notation used for divergence comes from considering \(\nabla\) as a differential operator, as follows.

$$\nabla \cdot \textbf{F}(x,y,z)$$	$$=\left[ \left( \frac{\partial }{\partial x} \right)\text{i} + \left( \frac{\partial }{\partial y} \right)\text{j} + \left( \frac{\partial }{\partial z} \right)\text{k}\right] \cdot (M\text{i} + N\text{j} + P\text{k}) $$
	$$= \frac{\partial M}{\partial x} + \frac{\partial N}{\partial y} + \frac{\partial P}{\partial z} $$

Example 15.1.9 Finding the Divergence for a Vector Field

Find the divergence at (2,1,-1) for the vector field

\(\textbf{F}(x,y,z)=x^{3}y^{2}z\textbf{i} +x^{2}z\textbf{j}+x^{2}y\textbf{k}\).

Solution The divergence for \(\textbf{F}\) is

$$\text{div }\textbf{F}(x,y,z) = \frac{\partial }{\partial x}[x^{3}y^{2}z] + \frac{\partial }{\partial y}[x^{2}y] + \frac{\partial }{\partial z}[x^{2}y]=3x^{2}y^{2}z. $$

The divergence at the point (2,1,-1) is

div \( \textbf{F}(\color{red}{2},\color{red}{1},\color{red}{-1}) = 3(\color{red}{2}^{2})(\color{red}{1}^{2})(\color{red}{-1})=-12. \)

Divergence is an \( \textbf{F}\) derivative variant that measures the flow rate per unit volume at a point using vector fields. In fluid dynamics a velocity field that is divergence free is called incompressible. In electromagnetism a vector field that is divergence free is called solenoidal.

Theorem 15.1.3 Divergence and Curl

If \(\textbf{F}(x,y,z)=M\textbf{i} +N\textbf{j}+P\textbf{k}\) is a vector field and \(M\), \(N\), and \(P\) have continuous second partial derivatives, then

\(\text{div } (\text{curl }\textbf{F})= 0\).

Internal Links

Parent Article: Calculus III 15 Vector Analysis