Calculus II 08.02 Integration by Parts

Previous	Calculus II 08.01 Basic Integration Rules
Next	Calculus II 08.03 Trigonometric Integrals

8.2 Integration by Parts

• Find an antiderivative using integration by parts.

Integration by Parts

Integration by parts is useful for integrands with algebraic and transcendental function that have products. Some examples are

$$ \int x \ln x\:dx ,\: \int x^{2}e^{x}\:dx \text{, and } \int e^{x} \sin x\:dx $$

Integration by parts is based on finding the derivative for a product. To review

$$ \frac{d}{dx}[uv] $$	$$= u \frac{dv}{dx}+v \frac{du}{dx} $$
	\(= uv^{\prime}+vu^{\prime} \)

where \(u\) and \(v\) are differentiable functions for \(x\). When \(u^{\prime}\) and \(v^{\prime}\) are continuous, both sides can be integrated to produce

\(uv \)	$$= \int uv^{\prime}\:dx + \int vu^{\prime}\:dx $$
	$$ = \int u \:dv + \int v\:du .$$

This leads to Theorem 8.2.1 below

Theorem 8.2.1 Integration by Parts

If \(u\) and \(v\) are functions for \(x\) and have continuous derivatives, then

$$ \int u\:dv =uv - \int v\:du $$

This formula expresses the original integral in terms from another integral. Depending on the choices for \(u\) and \(dv\), it may be easier to evaluate the second integral than the original one. Because the theorem depends on the choices made for \(u\) and \(dv\) the guidelines below are provided.

Guidelines for Integration by Parts

1. "L-I-A-T-E" Choose \(u\) from the first in this list: L: Logrithmic Function I: Inverse Trig Function A: Algebraic Function T: Trig Function E: Exponential Function

2. Let \(dv\) be the most complex integrand part that fits a basic integration rule. Then \(u\) will be the integrand's remaining factor(s).

3. Let \(u\) be the part where \(du\) is simpler, or easier to solve, than \(u\) is.

Note that \(dv\) always include the \(dx\) from the original integrand.

Example 8.2.1 Integration by Parts using the Product Rule

Find

$$ \int xe^{x}\:dx .$$

Solution Write the integral in the form \(\int u \:dv\). Here are four choices.

$$\textbf{a. }\int \color{red}{\underbrace{\color{black}{(x)}}_{\color{red}{\text{u}}}} \color{red}{\underbrace{\color{black}{\left(e^{x}dx \right)}}_{\color{red}{\text{dv}}}},$$

$$\textbf{b. }\int \color{red}{\underbrace{\color{black}{(e^{x})}}_{\color{red}{\text{u}}}}\color{red}{\underbrace{\color{black}{(x\:dx)}}_{\color{red}{\text{dv}}}},$$

$$\textbf{c. }\int \color{red}{\underbrace{\color{black}{(1)}}_{\color{red}{\text{u}}}}\color{red}{\underbrace{\color{black}{(xe^{x}dx)}}_{\color{red}{\text{dv}}}}, $$

$$\textbf{d. }\int \color{red}{\underbrace{\color{black}{(1)}}_{\color{red}{\text{u}}}}\color{red}{\underbrace{\color{black}{(xe^{x}dx)}}_{\color{red}{\text{dv}}}}.$$

Theorem 8.2.1 suggests a. because \(x\:dx\) is simpler than \(x\), and \(dv=e^{x}\) is more complex.

\(dv\)	\(=e^{x}dx\)	\(\rightarrow\)	\( v=\displaystyle{ \int } dv = \displaystyle{ \int } e^{x}dx=e^{x} \)
\(u\)	\(=x\)	\(\rightarrow\)	\( du=dx \)

Integration by Parts produces

$$ \int u\:dv $$	$$ =uv-\int v\:du $$	Integration by Parts Formula
$$ \int xe^{x} \:dx $$	$$=xe^{x} - \int xe^{x}\:dx \:\:\:\: $$	Substitute
	\(=xe^{x} - xe^{x}+C\)	Integrate

Example 8.2.2 Integration by Parts with Exponents and Natural Logs

Find

$$ \int x^{2} \ln x \: dx .$$

Solution The \(x^{2}\) equation is easier to integrate than \(\ln x\). The derivative for \(\ln x\) is simpler than \(\ln x\). Chose \(dx=x^{2}\:dx\).

$$dv =x^{2}\:dx \rightarrow v = \int x^{2}\:dx = \frac{x^{3}}{3} $$

$$u =\ln x \rightarrow du =\frac{1}{x}\:dx $$

Integration by parts produces

$$ \int u\:dv $$	$$=uv- \int v \: du $$	Integration by parts formula
$$ \int x^{2}\ln x \: dx $$	$$= \frac{x^{3}}{3} \ln x - \int \left( \frac{x^{3}}{3} \right) \left( \frac{1}{x} \right) dx \:\:\:\: $$	Substitute
	$$= \frac{x^{3}}{3} \ln x - \frac{1}{3} \int x^{2}\: dx $$	Simplify
	$$= \frac{x^{3}}{3} \ln x - \frac{x^{3}}{9} + C $$	Integrate

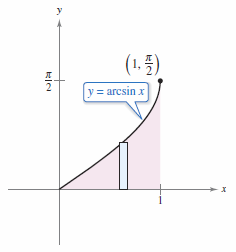
Example 8.2.3 An Integrand with a Single Complex Term

The region's area is \(\approx\) 0.571. Figure 8.2.1

In applying Integration by Parts to a single complex term such as $$ \int \ln x \:dx \text{ or } \int \arcsin x\:dv.$$ Let \(dv=dx\). Evaluate $$ \int_{0}^{1} \arcsin x\:dx.$$ Solution Let \(dv=dx\). \(dv\) \(=dx\) \( \rightarrow \) \(v\) $$= \int dx = x $$ \(u\) \(= \arcsin x\) \( \rightarrow \) \(du\) $$= \frac{1}{\sqrt{1-x^{2}}}dx $$ Integration by parts produces $$ \int u\:dv $$ $$=uv-\int v \: du $$ Integration by parts formula $$ \int \arcsin x \:dx $$ $$=x \arcsin x - \int \frac{x}{\sqrt{1-x^{2}}} \: dx $$ Substitute $$=x \arcsin x + \frac{1}{2} \int (1-x^{2})^{1/2}(-2x) \: dx \:\:\:\: $$ Rewrite \(=x \arcsin x + \sqrt{ 1-x^{2}} + C \) Integrate The definite integral can be evaluated as shown. $$ \int_{0}^{1} \arcsin x\:dx $$ $$= \left[ x \arcsin x + \sqrt{ 1-x^{2}} \right]_{0}^{1} $$ $$= \frac{\pi}{2}-1 \approx 0.571 $$ The area represented by this definite integral is shown in Figure 8.2.1.

Example 8.2.4 Integration by Parts, Repeated

Sometimes applying Integration by Parts just once, is not enough.
Find

$$ \int x^{2} \sin x \: dx .$$

Solution The factors \(x^{2}\) and \(\sin x\) are equally easy to integrate. The derivative for \(\sin x\) is more complex, but \(x^{2}\:dx\) is simpler. Let \(u=x^{2}\) in the first round.

\(dv\)	\(= \sin x\:dx\)	\( \rightarrow \)	\(v\)	$$= \int \sin x\:dx $$	\(= - \cos x \)
\(u\)	\(=x^{2} \)	\( \rightarrow \)	\(du\)	\(=2x\:dx \)

Integration by parts, round one, produces

$$ \int x^{2} \sin x \: dx = - x^{2} \cos x + \int 2x \cos x \:dx $$

Round one succeeded in simplifying the original integrand. But the new integral does not fit a basic integration rule. To further simplify it, apply integration by parts again, round two, with \(u=2x\).

\(dv\)	\(= \cos x\:dx\)	\( \rightarrow \)	\(v\)	$$= \int \cos x\:dx $$	\(= \sin x \)
\(u\)	\(=2x \)	\( \rightarrow \)	\(du\)	\(=2\:dx \)

Integration by parts, round two, produces

$$ \int 2x \cos x \:dx $$	$$=2x \sin x - \int 2 \sin x \: dx $$
	\(=2x \sin x + 2 \cos x + C \)

Combining both rounds produces

$$ \int x^{x} \sin x \:dx = -x^{2} \cos x + 2x \sin x + 2 \cos x + C $$

When using integration by parts repeatedly, do not interchange the substitutions in successive rounds.

For instance, in Example 8.2.4, the first substitution was \(u=x^{2}\) and \(dv= \sin x\:dx \). In the second round, if the substitution was switched to \(u= \cos x\) and \(dv=2x\) would have produced

$$ \int x^{2} \sin x \:dx $$	$$=-x^{2} \cos x + \int 2x \cos x \: dx $$
	$$= -x^{2} \cos x + x^{2} \cos x + \int x^{2} \sin x \: dx $$
	$$= \int x^{2} \sin x \: dx$$

thereby undoing the previous integration and returning to the original integral. Watch for a constant multiple in the original integral. In Example 8.2.5 there is a constant multiple hidden in the integral. In Example 8.4.5 it can be used to find the arc length for a parabolic segment.

Example 8.2.5 Integration by Parts with a hidden constant multiple

Find

$$ \int \sec^{3} x\:dx .$$

Solution The equation \(\sec^{2} x \) is easier to integrate than \(\sec^{3} x \) so let \(dv= \sec^{2} x\:dx \) and \(u= \sec x \).

\(dv\)	\(= \sec^{2} x\:dx\)	\( \rightarrow \)	\(v\)	$$= \int \sec^{2} x\:dx $$	\(= \tan x \)
\(u\)	\(=\sec x \)	\( \rightarrow \)	\(du\)	\(=\sec x \tan x \:dx \)

Integration by parts produces

$$ \int u\:dv $$	$$=uv- \int v \: du $$	Integration by parts formula
$$ \int \sec^{3} x \:dx $$	$$= \sec x \tan x - \int \sec x \tan^{2} x \: dx $$	Substitute
$$ \int \sec^{3} x \:dx $$	$$= \sec x \tan x - \int \sec x ( \sec^{2} x - 1) \: dx $$	Trigonometric identity
$$ \int \sec^{3} x \:dx $$	$$= \sec x \tan x - \int \sec^{3} x\:dx + \int \sec x \: dx \:\:\:\: $$	Rewrite
$$ 2 \int \sec^{3} x \:dx $$	$$= \sec x \tan x + \int \sec x \: dx $$	Collect like integrals. The constant multiple appears.
$$ 2 \int \sec^{3} x \:dx $$	$$= \sec x \tan x + \ln | \sec x + \tan x | + C $$	Integrate
$$ \int \sec^{3} x \:dx $$	$$= \frac{1}{2}\sec x \tan x + \frac{1}{2}\ln | \sec x + \tan x | + C $$	Divide by 2.

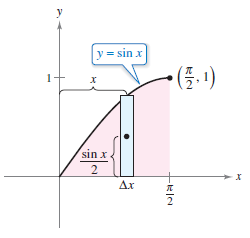
Example 8.2.6 Finding a Centroid

Figure 8.2.2

A machine part is modeled by the region bounded by the graph between \(y=\sin x\), the \(x\)-axis, and \(0\leqslant x \leqslant \pi/2\), as shown in Figure 8.2.2. Find the centroid for this region. Solution Begin by finding the region's area. $$A = \int_{0}^{\pi/2} \sin x\:dx = \bigg[ -\cos x \bigg]_{0}^{\pi/2} = 1 $$ Now for the centroid's coordinates. To evaluate the integral for \(\bar{y}\), first rewrite the integrand using the trigonometric identity \(\sin^{2} x = (1- \cos 2x)/2\). $$\bar{y}=\frac{1}{A} \int_{0}^{\pi/2} \frac{\sin x}{2}(\sin x)\:dx = \frac{1}{4} \int_{0}^{\pi/2} (1- \cos 2x)\:dx = \frac{1}{4} \left[ x - \frac{\sin 2x}{2} \right]_{0}^{\pi/2} = \frac{\pi}{8} $$ Evaluating the integral for \(\bar{x}\), $$(1/A)\int_{0}^{\pi/2} x \sin x\:dx ,$$ with integration by parts. Let \(dv=\sin x\:dx\) and \(u=x\). This produces \(v=-\cos x\) and \(du=dx\), and can be written as $$ \int x \sin x\:dx= -x \cos x + \int \cos x \: dx = -x \cos x + \sin x + C $$ Evaluating \(\bar{x}\) reduces to $$ \bar{x} = \frac{1}{4} \int_{0}^{\pi/2} x \sin x\:dx = \bigg[ -x \cos x + \sin x \bigg]_{0}^{\pi/2} = 1 $$ The region's centroid is \((1,\pi / 8) \).

Common Integrals using Integration by Parts

1. For integrals with the form

$$ \int x^{n} e^{ax}\:dx \text{, } \int x^{n} \sin ax\:dx \text{, or } \int x^{n} \cos ax\:dx $$

let \(u=x^{n}\) and let \(dv=e^{ax}\:dx\), \( \sin ax\:dx\), or \( \cos ax\:dx\).
2. For integrals with the form

$$ \int x^{n} \ln x\:dx \text{, } \int x^{n} \arcsin ax\:dx \text{, or } \int x^{n} \arctan ax\:dx $$

let \(u=\ln x\), \(\arcsin ax\), or \(\arctan ax\) and let \(dv=x^{n}\:dx\).
3. For integrals with the form

$$ \int e^{ax} \sin bx\:dx \text{ or } \int e^{ax} \cos bx\:dx $$

let \(u=\sin bx\) or \( \cos bx\) and let \(dv=e^{ax}\:dx\).

Example 8.2.7 Using the Tabular Method

In problems where integration by parts is applied repeatedly, a tabular method can help to organize the work. This method works well for integrals with the form

$$ \int x^{n} e^{ax}\:dx, \: \int x^{n} \sin ax\:dx \text{, or } \int x^{n} \cos ax\:dx$$

Find \( \displaystyle{ \int } x^{2} \sin 4x\:dx\).
Solution Let \(u=x^{2}\) and \(dv={v}'\:dx=\sin 4x\:dx\). Then create a table with three columns as shown in Figure 8.2.3.

Figure 8.2.3

The solution is found by adding the signed products along the diagonal entries:

$$ \int x^{2} \sin 4x\:dx = -\frac{1}{4} x^{2} \cos 4x + \frac{1}{8} x \sin 4x + \frac{1}{32} \cos 4x + C$$

Internal Links

Parent Article: Calculus II 08 Integration Techniques