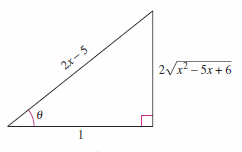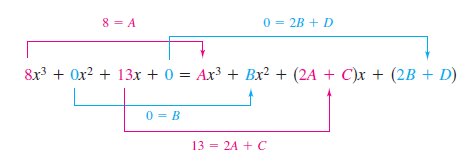Calculus II 08.05 Partial Fractions
| Previous | Calculus II 08.04 Trigonometric Substitution |
| Next | Calculus II 08.06 Integration by Tables and Other Integration Techniques |
Contents
8.5 Partial Fractions
- Partial fraction decomposition
- Partial fraction decomposition with linear factors to integrate rational functions
- Partial fraction decomposition with quadratic factors to integrate rational functions
Partial Fractions
|
Partial fraction decomposition is a method for decomposing a single rational function into many simpler rational functions so the basic integration formulas can be applied. This procedure is called the method of partial fractions. For our purposes we will call it partial fraction decomposition. Consider the following integral
To evaluate this integral without partial fractions,complete the square and use trigonometric substitution, see Figure 8.5.1, to obtain
Note that the fraction can be broken into two smaller pieces
The integral evaluates more easily as the natural log is applied directly to each fraction.
|
This method is clearly preferable to trigonometric substitution. However, it depends on factoring the denominator evenly. In this case, factoring the \(x^{2}-5x-6\) denominator into the partial fractions
- $$ \frac{1}{x-3} \text{ and } - \frac{1}{x-2} .$$
This section describes techniques for finding partial fraction decompositions.
Recall from algebra that every real polynomial[1] with real coefficients can be factored into linear and irreducible quadratic factors. Consider the polynomial
- $$x^{5}+x^{4}-x-1$$
can be written as
| \( x^{5}+x^{4}-x-1 \) | \(= x^{4}(x+1)-(x+1) \) |
| \(= (x^{4}+1)(x+1) \) | |
| \(= (x^{2}+1)(x^{2}-1)(x+1) \) | |
| \(= (x^{2}+1)(x+1)(x-1)(x+1) \) | |
| \(= (x-1)(x+1)^{2}(x^{2}+1) \) |
where \( (x-1) \) is a linear factor, \( (x+1)^{2} \) is a repeated linear factor, and \((x^{2}+1) \) is an irreducible quadratic factor.
Using this factorization, you can write the partial fraction decomposition of the rational expression
- $$ \frac{N(x)}{x^{5}+x^{4}-x-1} $$
where \( N(x) \) is a polynomial with a degree five or less. This breaks down into
- $$ \frac{N(x)}{(x-1)(x+1)^{2}(x^{2}+1)} = \frac{A}{x-1}+\frac{B}{x+1}+\frac{C}{(x+1)^{2}} + \frac{Dx+E}{x^{2}+1} $$
Decomposing \( N(x)/D(x)\) into Partial Fractions
1. Divide when improper: When \( N(x)/D(x)\) is an improper fraction -- the numerator's degree is greater than or equal to the denominator's degree -- divide the denominator into the numerator to obtain
- $$ \frac{N(x)}{D(x)}= (\text{a polynomial}) + \frac{N(x)_{1}}{D(x)} $$
where \( N(x)_{1} \)'s degree is less than \( D(x) \)'s degree. Then apply Steps 2, 3, and 4 to the proper rational expression \( N(x)/D(x)\).
2. Factor denominator: Completely factor the denominator into factors with the form
- $$ (px+q)^{m} \text{ and } (ax^{2}+bx+c)^{n} $$
where \( ax^{2}+bx+c \) is irreducible.
3. Linear factors: For each factor with the form \( (px+q)^{m} \), the partial fraction decomposition must include the following \(m\) summation fractions.
- $$ \frac{A_{1}}{(px+q)}+\frac{A_{2}}{(px+q)^{2}}+ \cdots + \frac{A_{m}}{(px+q)^{m}} $$
4. Quadratic factors: For each factor with the form \( (ax^{2}+bx+c)^{n} \), the partial fraction decomposition must include the following \(n\) summation fractions.
- $$ \frac{B_{1}x+C_{1}}{ax^{2}+bx+c}+\frac{B_{2}x+C_{2}}{(ax^{2}+bx+c)^{2}}+ \cdots + \frac{B_{n}x+C_{n}}{(ax^{2}+bx+c)^{n}} $$
Linear Factors
Algebraic techniques for determining the constants in the numerators for a partial fraction decomposition with linear or repeated linear factors are shown in Examples 8.5.1 and 8.5.2.
Example 8.5.1 Distinct Linear Factors
Write the partial fractions decomposition for
- $$ \frac{1}{x^{2}-5x+6}. $$
Solution Because \( x^{2}-5x+6 = (x-3)(x-2) \), include one partial fraction for each factor and write
- $$ \frac{1}{x^{2}-5x+6} = \frac{A}{x-3} + \frac{B}{x-2} $$
where \(A\) and \(B\) are to be determined. Multiply by the last common denominator \( (x-3)(x-2) \) yields the basic equation.
| $$ 1=A(x-2)+ B(x-3) \:\:\:\: $$ | Basic equation |
Since this equation is true for all \(x\), any convenient values for \(x\) can be used to obtain equations in \(A\) and \(B\). The most convenient values are the ones that make particular factors equal to 0. height:100px; To solve for \(A\), let \(x=3\).
| \( 1=A(\color{red}{3}-2)+ B(\color{red}{3}-3) \:\:\:\: \) | Let \(x=3\) in the basic equation |
| \( 1=A(1)+ B(0) \) | |
| \( 1 = A \) |
To solve for \(B\), let \(x=2\).
| \( 1=A(\color{red}{2}-2)+ B(\color{red}{2}-3) \:\:\:\: \) | Let \(x=2\) in the basic equation |
| \( 1=A(0)+ B(-1) \) | |
| \( -1=B \) |
This decomposition
- $$ \large \frac{1}{x^{2}-5x+6} = \frac{1}{x-3} + \frac{1}{x-2} $$
agrees with the answer using trigonometric substitution.
Partial fractions works only where the denominator factors evenly. For instance, when the denominator in Example 8.5.1 is changed to
- $$ \large x^{2}-5x+5 $$
it factors to
- $$ x^{2}-5x+5 = \left[ x-\frac{5+\sqrt{5}}{2} \right] \left[ x-\frac{5-\sqrt{5}}{2} \right]$$
which is too cumbersome for partial factions. Instead use completing the square to perform the integration. This produces
- $$ \int \frac{1}{x^{2}-5x+5}dx= \frac{\sqrt{5}}{5} \ln \left| 2x-\sqrt{5}-5 \right | - \frac{\sqrt{5}}{5} \ln \left | 2x + \sqrt{5}-5 \right | + C. $$
Example 8.5.2 Repeated Linear Factors
Find
- $$ \int \frac{5x^{2}+20x+6}{x^{3}+2x^{2}+x}\:dx $$
Solution The denominator factors out evenly to
- $$ x^{3}+2x^{2}+x = x(x^{2}+2x+1)=x(x+1)^{2}$$
include one fraction for each \( x\) power and \((x+1)\) then write
- $$ \frac{5x^{2}+20x+6}{x(x+1)^{2}} = \frac{A}{x} + \frac{B}{x+1} + \frac{C}{(x+1)^{2}}. $$
Multiplying by the least common denominator, \( x(x+1)^{2} \) yields the basic equation
| $$ x(x+1)^{2} \:\:\:\: $$ | Basic equation |
To solve for \( A \), let \( x = 0\). This eliminates the \( B \) and \( C \) terms and yields
| \( 6\) | \(= A(1) +0+0\) |
| \(6\) | \(= A\). |
To solve for \( C \), let \(x=-1\). The eliminates the \(A\) and \(B\) terms and yields
| \( 5-20+6\) | \(=0+0-C\) |
| \(9\) | \(=C \) |
The most convenient choices for \(x\) have been used, so to find \(B\)'s value, you can use any other value for \(x\) along with the calculated values for \(A\) and \(C\). Using \(x = 1\), \(A = 6\), and \(C = 9\) produces
| \(5+20+6\) | \(= A(4)+B(2)+C\) |
| \(31\) | \(= 6(4)+2B+9\) |
| \(-2\) | \(= 2B\) |
| \(-1\) | \(= B\). |
Back substitution produces
| $$ \int \frac{5x^{2}+20x+6}{x^{3}+2x^{2}+x}\:dx $$ | $$= \large \int \left( \frac{6}{x}- \frac{1}{x+1}+ \frac{9}{(x+1)^{2}} \right)\:dx $$ |
| $$= \large 6 \ln|x| - \ln|x+1| + 9 \frac{(x+1)^{-1}}{-1} +C $$ | |
| $$= \large \ln \left|\frac{x^{6}}{x+1}\right| - \frac{9}{x+1} + C $$ |
It is necessary to make as many substitutions for \(x\) as there are unknowns \((A, B, C, . . .)\) to be determined. In Example 8.5.2, three substitutions \(x = 0\), \(x = -1\), and \(x = 1\) were made to solve for \(A \), \(B\), and \(C\).
Quadratic Factors
When using partial fractions with linear factors, a convenient choice for \(x\) immediately yields a value for a coefficient. With quadratic factors, a system of linear equations usually must be solved, no matter what value is chosen for \(x\).
Example 8.5.3 Distinct Linear and Quadratic Factors
Find \( \large \displaystyle{ \int } \frac{2x^{3}-4x-8}{(x^{2}-x)(x^{2}+4)}\:dx \)
Solution The denominator factors to
- $$(x^{2}-x)(x^{2}+4) = x(x-1)(x^{2}+4). $$
Include one partial fraction for each factor and write
- $$ \frac{2x^{3}-4x-8}{(x^{2}-x)(x^{2}+4)} = \frac{A}{x} + \frac{B}{x-1} + \frac{Cx+D}{x^{2}+4}. $$
Multiplying by the least common denominator
- $$ x(x-1)(x^{2}+4) $$
yields the basic equation
- $$ 2x^{3}-4x-8 = A(x-1)(x^{2}+4) + Bx(x^{2}+4) + (Cx+D)(x)(x-1).$$
To solve for \(A\), let \(x=0\) and obtain
| \(-8\) | \(=A(-1)(4)+0 +0 \) |
| \(2\) | \(=A \) |
To solve for \(B\), let \(x=1\) and obtain
| \(-10\) | \(=0+B(5)+0 \) |
| \(-2\) | \(=B \) |
Choose two other values for \(x\) and solve the linear equations to find \(C\) and \(D\). Using \(x=-1\), \(A=2\), and \(B=-2\) produces
| \(-6\) | \(=(2)(-2)(5)+(-2)(-1)(5)+(-C+D)(-1)(-2) \) |
| \(2\) | \(=-C+D\) |
Let \(x=2\) produces
| \(0\) | \(=(2)(1)(8)+(-2)(2)(8)+(2C+D)(2)(1) \) |
| \(8\) | \(=2C+D\) |
Solving the linear system by subtracting the first equation from the second
| \(-C+D\) | \(=2 \) |
| \(2C+D\) | \(=8\) |
yields \(C=2\) and \(D=4\). Back substitution produces
| $$ \int \frac{2x^{3}-4x-8}{(x^{2}-x)(x^{2}+4)}\:dx $$ | $$= \int \frac{2}{x}-\frac{2}{x-1}+\frac{2x}{x^{2}+4}+\frac{4}{x^{2}+4} \:dx $$ |
| $$= 2\ln|x|-2\ln|x-1| + \ln(x^{2}+4)+2\arctan \frac{x}{2}+C .$$ |
Example 8.5.4 Repeated Quadratic Factors
Find
- $$ \int \frac{8x^{3}+13x}{(x^{2}+2)^{2}}\:dx .$$
Solution Repeated substitution worked on the preceding linear examples. This equation has only quadratic factors so a new method is needed. Write the basic equation's right side in polynomial form and equating the coefficients for like terms.
Include one partial fraction for each power of \( (x^{2}+2) \) and write
- $$ \frac{8x^{3}+13x}{(x^{2}+2)^{2}} = \frac{Ax+B}{x^{2}+2} + \frac{Cx+D}{(x^{2}+2)^{2}}. $$
Multiplying by the least common denominator, \( (x^{2}+2)^{2} \), yields the basic equation
- $$ 8x^{3}+13x = (Ax+B)(x^{2}+2) + Cx+D. $$
Expanding the basic equation and collecting like terms produces
- $$ 8x^{3}+13x = Ax^{3}+2Ax+Bx^{2}+2B + Cx+D $$
- $$ 8x^{3}+13x = Ax^{3}+Bx^{2}+(2A+C)x+(2B+D).$$
Equate the coefficients for like terms on opposite sides.
Using the known values \(A=8\) and \(B=0\) produces
- $$13=2A+C\rightarrow 13=2(8)+C\rightarrow -3=C $$
- $$0=2B+D\rightarrow 0=2(0)+D\rightarrow 0=D $$
Back substitution produces
| $$ \int \frac{8x+13x}{(x^{2}+2)^{2}}\:dx $$ | $$= \int \left( \frac{8x^{3}}{x^{2}+2} + \frac{-3x}{(x^{2}+2)^{2}} \right) \:dx $$ |
| $$ \large = 4\ln(x^{2}+2)+ \frac{3}{2(x^{2}+2)} +C. $$ |
When integrating rational improper expressions such as
- $$ \frac{N(x)}{D(x)}=\frac{2x^{3}+x^{2}-7x+7}{x^{2}+x-2} $$
first divide to obtain a proper expression
- $$ \frac{N(x)}{D(x)}=-2x-1+\frac{-2x+5}{x^{2}+x-2}. $$
The proper rational expression is then decomposed into its partial fractions.
Here are some guidelines for solving the basic equation that is obtained in a partial fraction decomposition.
Guidelins for Solving the Basic Equation by Partial Fraction Decomposition
Linear Factors
1. Substitute the roots of the distinct linear factors in the basic equation with integers.
2. For repeated linear factors, use the coefficients determined in the first guideline to rewrite the basic equation. Then substitute other convenient values for \(x\) and solve for the remaining coefficients.
Quadratic Factors
1. Expand the basic equation.
2. Collect terms according to powers for \(x\).
3. Equate the coefficients for like powers to obtain linear equations involving \(A,B,C,...\)
4. Solve the linear equations.
It is not necessary to use the partial fractions technique on all rational functions. The integral below is more easily evaluated using the Log Rule.
| $$ \int \frac{x^{2}+1}{x^{3}+3x-4}\:dx $$ | $$= \frac{1}{3} \int \frac{3x^{2}+3}{x^{3}+3x-4} \:dx $$ |
| $$ = \frac{1}{3} \ln|x^{3}+3x-4|+C $$ |
When the integrand is not in a reduced form, reducing it may eliminate the need for partial fractions, as shown in the following integral.
| $$ \int \frac{x^{2}-x-2}{x^{3}-2x-4}\:dx $$ | $$= \int \frac{(x+1)(x-2)}{(x-2)(x^{2}+2x+2)} \:dx $$ |
| $$ = \int \frac{x+1}{x^{2}+2x+2} \:dx $$ | |
| $$ = \frac{1}{2} \ln |x^{2}+2x+2|+C $$ |
Partial fractions can be used with some quotients involving transcendental functions. For instance, the substitution \(u=\sin x\) allows you to write
| $$ \int \frac{\cos x}{\sin x(\sin x-1)}\:dx $$ | $$= \int \frac{du}{u(u-1)} \:\:\:\: $$ | \(u=\sin x, du=\cos x\:dx.\) |
Internal Links
Parent Article: Calculus II 08 Integration Techniques