Calculus II 09.07 Taylor Polynomials and Approximations

Previous	Calculus II 09.06 The Ratio and Root Tests
Next	Calculus II 09.08 Power Series

9.7 Taylor Polynomials[1] and Approximations

• Find polynomial approximations for elementary functions.
• Find Taylor and Maclaurin polynomial approximations for elementary functions.
• Use the remainder from a Taylor polynomial.

Polynomial Approximations for Elementary Functions

Near \((c,f(c))\) the graph for \(P\) can be used to approximate the graph for \(f\). Figure 9.7.1

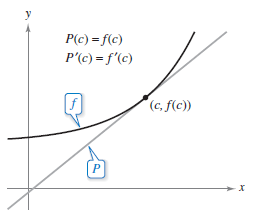
Polynomial functions can be used as approximations for other elementary functions. To find a polynomial \(P\) function that approximates another function \(f\), begin by choosing a number \(c\) in \(f\)'s domain at which \(f\) and \(P\) have the same value and the same slope. That is. $$1.\: P(c)=f(c) \:\:\:\:\:\:\: \color{red}{\text{ Graphs for \(f\) and \(P\) pass through \((c,f(c))\)}}$$ $$2.\: P'(c)=f'(c) \:\:\:\: \color{red}{\text{ Graphs for \(f\) and \(P\) have the same slope at \((c,f(c))\)}}$$ The approximating polynomial is described as expanded about \(c\) or centered at \(c\). Geometrically, the requirement that \(P(c)=f(c)\) means that \(P\)'s graph passes through the point \((c,f(c))\). Since infinitely many graphs can pass through \((c,f(c))\) the slopes must be equal to produce a linear approximation for \(f\) as shown in Figure 9.7.1.

Example 9.7.1 First-Degree Polynomial Approximation for \(f(x)=e^{x}\)

\(P_{1}\) is the first-degree polynomial approximation for \(P\) can be used to approximate the graph for \(f(x)=e^{x}\). Figure 9.7.2

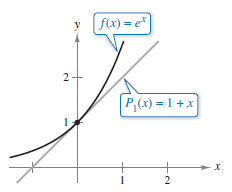
For \(f(x)=e^{x}\) find a first-degree polynomial function \(P_{1}(x)=a_{0}+a_{1}x\) whose value and slope agree with the value and slope for \(f\) at \(x=0\). Solution Because \(f(x)=e^{x}\) and \(f'(x)=e^{x}\), the value and slope for \(f\) at \(x=0\) are $$f(\color{red}{0})= e^{\color{red}{0}}=1\:\:\:\: \color{red}{ \text{ Value for } f \text{ at } x=0}$$ and $$f'(\color{red}{0})= e^{\color{red}{0}}=1.\:\:\:\: \color{red}{ \text{ Slope for } f \text{ at } x=0}$$ Because \(P_{1}(x)=a_{0}+a_{1}x\), you can use the condition that \(P_{1}(0)=f(0)\) to conclude that \(a_{0}=1\). Because \(P_{1}'(x)=a_{1}\), you can use the condition that \(P_{1}'(0)=f'(0)\) to conclude that \(a_{1}=1\). Therefore, \(P_{1}(x)=1+x\). Figure 9.7.2 shows the graphs for \(P_{1}(x)=1+x\) and \(f(x)=e^{x}\).

\(P_{2}\) is the second-degree polynomial approximation for \(f(x)=e^{x}\). Figure 9.7.3

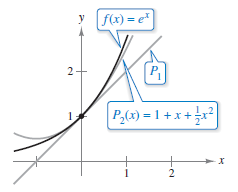
In Figure 9.7.3 points near (0,1), the graph for the first-degree polynomial function $$P_{1}(x)=1+x \:\:\:\: \color{red}{\text{ 1st-degree approximation}}$$ is reasonably close to the graph for \(f(x)=e^{x}\). Moving either way along the 1st-degree graph away from (0,1) and the approximation's accuracy decreases. To improve the approximation another requirement is needed. That the second derivatives for \(P\) and \(f\) agree when \(x=0\). The polynomial, \(P_{1}\), with the least degree that satisfies all three requirements, \(P_{2}(0)=f(0)\), \(P_{2}^{"}(0)=f{}'(0)\), and \( P_{2}^{"} (0)=f^{"} (0) \) is $$P_{2}(x)=1+x+\frac{1}{2}x^{2} \:\:\:\: \color{red}{\text{ 2nd-degree approximation}}$$ as shown in Figure 9.7.3. By extending this method to the first \(n\) derivatives that math \(f(x)=e^{x}\) at \(x=0\), produces the \(n\)th-degree approximation. $$P_{n}(x)$$ $$=1+x+\frac{1}{2}x^{2}+\frac{1}{3!}x^{3}+\cdots++\frac{1}{n!}x^{n} \:\:\:\: \color{red}{\text{ \(n\)th-degree approximation}}$$ $$\approx e^{x}$$

Example 9.7.2 Third-Degree Polynomial Approximation for \(f(x)=e^{x}\)

\(P_{3}\) is the third-degree polynomial approximation for \(f(x)=e^{x}\). Figure 9.7.4

Construct a table comparing the values for the polynomial $$P_{3}(x)=1+x+\frac{1}{2}x^{2}+\frac{1}{3!}x^{3} \:\:\:\: \color{red}{\text{ 3rd-degree approximation}}$$ with \(f(x)=e^{x}\) where \(x\) is several values near 0. Solution Using a computer produces the results in Table 9.7.1. For \(x=0\) the functions agree, but as \(x\) moves farther away from 0, the polynomial \(P_{3}\)'s approximation decreases. This is shown graphically in Figure 9.7.4 Table 9.7.1 \(P_{3}\) approximations \(x\) -1.0 -0.2 -0.1 0 0.1 0.2 1.0 \(e^{x}\) 0.3679 0.81873 0.904837 1 1.105171 1.22140 2.7183 \(P_{3}(x)\) 0.3333 0.81867 0.904833 1 1.105167 1.22133 2.6667

Taylor and Maclaurin[2] Polynomials

The polynomial approximation for

$$f(x)=e^{x}$$

in Example 9.7.2 is expanded about the point \(c=0\). For expansions about an arbitrary value for \(c\), it is convenient to write the polynomial in the form

$$P_{3}(x)=a_{0}+a_{1}(x-c)+a_{2}(x-c)^{2}+a_{3}(x-c)^{3}+\cdots+a_{n}(x-c)^{n}.$$

Using this form repeated differentiation can be described as

\(P_{n}{}^{\prime}(x)\)	\(= a_{1}+2a_{2}(x-c)+3a_{3}(x-c)^{2}+\cdots+n(n-1)a_{n}(x-c)^{n-1} \)
\(P_{n}{}^{\prime \prime}(x)\)	\(= 2a_{2}+2(3a_{3})(x-c)+\cdots+n(n-1)a_{n}(x-c)^{n-2} \)
\(P_{n}{}^{\prime \prime \prime}(x)\)	\(= 2(3a_{3})+\cdots+n(n-1)(n-2)a_{n}(x-c)^{n-3}\)
	\( \vdots\)
\(P_{n}{}^{(n)}(x)\)	\(=n(n-1)(n-2)\cdots(2)(1)a_{n}. \)

Letting \(x=c\) yields

\( P_{n}(c)=a_{1},\:\:P_{n}{}^{\prime }(c)= a_{1},\:\:P_{n}{}^{\prime \prime}(c)= 2a_{2},...,\:\:P_{n}{}^{(n)}(c)= n!a_{n} \)

and because the values for \(f\) and its first \(n\) derivatives must agree with the values for \( P_{n}\) and its first \(n\) derivatives at \(x=c\), it follows that

\( f(c)=a_{1},\:\:f{}^{\prime }(c)= a_{1},\:\:\frac{f{}^{\prime \prime}(c)}{2!}= a_{2},...,\:\: \frac{f{}^{(n)}(c)}{n!}=a_{n}.\)

These coefficients are used to define Taylor polynomials, named after the English mathematician Brook Taylor[3], and Maclaurin polynomials, named after the English mathematician Colin Maclaurin[4].

Definition 9.7.1 Taylor and Maclaurin Polynomials

If \(f\) has \(n\) derivatives at \(c\), then the polynomial

$$ P_{n}(x)=f(c) +f{}^{\prime }(c)(x-c)+ \frac{f{}^{\prime \prime}(c)}{2!}(x-c)^{2}+\cdots+ \frac{f{}^{(n)}(c)}{n!}(x-c)^{n} $$

is called the \(n\)th Taylor polynomial for \(f\) at \(c\). If \(c=0\), then

$$ P_{n}(x)=f(0) +f{}^{\prime }(0)x+\frac{f{}^{\prime \prime}(0)}{2!}x^{2}+\frac{f{}^{\prime \prime \prime}(0)}{3!}x^{3}+\cdots+ \frac{f{}^{(n)}(0)}{n!}x^{n} $$

is also called the \(n\)th Maclaurin polynomial for \(f\).

Example 9.7.3 A Maclaurin Polynomial for \(f(x)=e^{x}\)

Find the \(n\)th Maclaurin polynomial for

$$ f(x)=e^{x}. $$

Solution From Definition 9.7.1, the \(n\)th Maclaurin polynomial is

$$ P_{n}(x)= 1 + x + \frac{1}{2!}x^{2}+\frac{1}{3!}x^{3}+\cdots+ \frac{1}{n!}x^{n}. $$

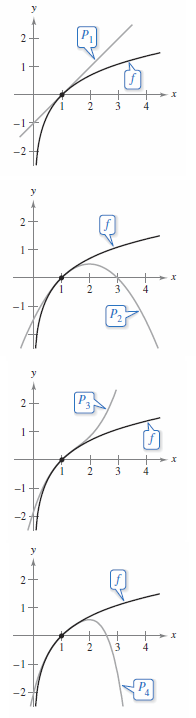
Example 9.7.4 Finding Taylor Polynomials for \(\ln x \)

The graph for \(P_{n}\) becomes a more accurate approximation for \(f(x)\)'s graph as \(n\) increases. Figure 9.7.5

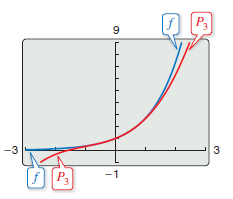
Find the Taylor polynomials \(P_{0}, \: P_{1},\: P_{2},\: P_{3},\:\text{ and } P_{4}\) for $$ f(x)=\ln x $$ centered at \(c=1\). Solution Expanding about \(c=1\) yields the following. $$ f(x)= \ln x $$ $$ f(\color{red}{1})= \ln \color{red}{1} = 0 $$ $$ f{}^{\prime }(x)=\frac{1}{x} $$ $$ f{}^{\prime }(\color{red}{1})=\frac{1}{\color{red}{1}} = 1 $$ $$ f{}^{\prime \prime }(x)=-\frac{1}{x^{2}} $$ $$ f{}^{\prime \prime }(\color{red}{1})=-\frac{1}{\color{red}{1}^{2}}= -1 $$ $$ f{}^{\prime \prime \prime }(x)=\frac{2!}{x^{3}} $$ $$ f{}^{\prime \prime \prime }(\color{red}{1})=\frac{2!}{\color{red}{1}^{3}}=2 $$ $$ f{}^{ (4) }(x)=-\frac{3!}{x^{4}}$$ $$ f{}^{ (4) }(\color{red}{1})=-\frac{3!}{\color{red}{1}^{4}}=-6 $$ Therefore, the Taylor polynomials are as follows. $$P_{0}(x) $$ $$=f(1)=0 $$ $$P_{1}(x) $$ $$=f(1)+ f{}^{\prime}(1)(x-1)=(x-1) $$ $$P_{2}(x) $$ $$=f(1)+ f{}^{\prime}(1)(x-1) + \frac{f{}^{\prime \prime}(1)}{2!}(x-1)^{2} $$ $$=(x-1)-\frac{1}{2}(x-1)^{2} $$ $$P_{3}(x) $$ $$=f(1)+ f{}^{\prime}(1)(x-1) + \frac{f{}^{\prime \prime}(1)}{2!}(x-1)^{2}+ \frac{f{}^{\prime \prime \prime}(1)}{3!}(x-1)^{3} $$ $$=(x-1)-\frac{1}{2}(x-1)^{2}+\frac{1}{3}(x-1)^{3} $$ $$P_{4}(x) $$ $$=f(1)+ f{}^{\prime}(1)(x-1) + \frac{f{}^{\prime \prime}(1)}{2!}(x-1)^{2}+ \frac{f{}^{\prime \prime \prime}(1)}{3!}(x-1)^{3} + \frac{f{}^{(4)}(1)}{4!}(x-1)^{4}$$ $$=(x-1)-\frac{1}{2}(x-1)^{2}+\frac{1}{3}(x-1)^{3}-\frac{1}{4}(x-1)^{4} $$ Figure 9.7.4 compares the graphs for \(P_{0}, \: P_{1},\: P_{2},\: P_{3},\:\text{ and } P_{4}\) with the graph for \(f(x)=\ln x\). Note that near \(x=1\), the graphs are nearly indistinguishable. For instance, $$ P_{4}(1.1) \approx 0.0953083$$ and $$ \ln(1.1) \approx 0.0953102.$$

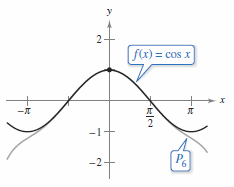
Example 9.7.5 Finding Maclaurin Polynomials for \(\cos x \)

Near (0,1), the graph for \(P_{6}\) can be used to approximate \(f(x)=\cos x\)'s graph. Figure 9.7.6

Find the Maclaurin polynomials \(P_{0}, \: P_{2},\: P_{4},\:\text{ and } P_{6}\) for \( f(x)=\cos x\). Use \(P_{6}(x)\) to approximate the value for \(\cos(0.1)\). Solution Expanding about \(c=0\) yields the following. \( f(x)= \cos x \) \( f(\color{red}{0})= \cos \color{red}{0} = 1 \) \( f{}^{\prime }(x)= -\sin x \) \( f{}^{\prime }(\color{red}{0}) =-\sin \color{red}{0} = 0 \) \( f{}^{\prime \prime }(x)=-\cos x \) \( f{}^{\prime \prime }(\color{red}{0})=-\cos \color{red}{0}= -1 \) \( f{}^{\prime \prime \prime }(x)=\sin x \) \( f{}^{\prime \prime \prime }(\color{red}{0})=\sin {\color{red}{0}}=0 \) Through repeated differentiation pattern 1, 0, -1, 0 continues, and produces the Maclaurin polynomials $$ P_{0}(x)=1, \: P_{2}(x)=1-\frac{1}{2!}x^{2},\: P_{4}(x)=1-\frac{1}{2!}x^{2}+\frac{1}{4!}x^{4} $$ and $$ P_{6}(x)=1-\frac{1}{2!}x^{2}+\frac{1}{4!}x^{4}-\frac{1}{6!}x^{6} $$ Using \(P_{6}(x)\) yields the approximation \(\cos(0.1) \approx 0.995004165\), which agrees with a computer calculation to nine decimal places. Figure 9.7.4 compares the graphs for \(f(x)=\cos x\) and \(P_{6}(x)\). Note in Example 9.7.5 that the Maclaurin polynomials for \( \cos x\) have only even powers for \(x\). Similarly, the Maclaurin polynomials for \( \sin x\) have only odd powers \(x\). This is not generally true for the Taylor polynomials for \( \sin x\) and \( \cos x \) expanded about \(c \ne 0\), as you can see in Example 9.7.6.

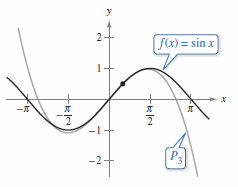
Example 9.7.6 Finding a Taylor Polynomial for \(\sin x \)

Near \((\pi/6,1/2) \), the graph for \(P_{3}\) can be used to approximate \(f(x)=\sin x\)'s graph. Figure 9.7.7

Find the third Taylor polynomials for \( f(x)=\sin x\), expanded about \(c=\pi/6\). Solution Expanding about \(c=\pi/6\) yields the following. \( f(x)= \sin x \) \( f(\color{red}{\frac{\pi}{6}})= \sin \color{red}{\color{red}{\frac{\pi}{6}}} = \frac{1}{2} \) \( f{}^{\prime }(x)= \cos x \) \( f{}^{\prime }(\color{red}{\frac{\pi}{6}}) =\cos \color{red}{\frac{\pi}{6}} = \frac{\sqrt{3}}{2} \) \( f{}^{\prime \prime }(x)=-\sin x \) \( f{}^{\prime \prime }(\color{red}{\frac{\pi}{6}})=-\sin \color{red}{\frac{\pi}{6}}= -\frac{1}{2} \) \( f{}^{\prime \prime \prime }(x)=-\cos x \) \( f{}^{\prime \prime \prime }(\color{red}{\frac{\pi}{6}})=-\cos \color{red}{\frac{\pi}{6}}=-\frac{\sqrt{3}}{2} \) The third Taylor polynomial for \(f(x)=\sin x\), about \(c=\pi/6\) is $$ P_{3}(x) $$ $$= f \left ( \frac{\pi}{6} \right ) + f{}^{\prime } \left ( \frac{\pi}{6} \right ) \left ( x-\frac{\pi}{6} \right ) + \frac{ f{}^{\prime \prime} \left ( \frac{\pi}{6} \right )}{2!} \left ( x-\frac{\pi}{6} \right )^{2} + \frac{ f{}^{\prime \prime} \left ( \frac{\pi}{6} \right )}{3!} \left ( x-\frac{\pi}{6} \right )^{3}$$ $$=\frac{1}{2} + \frac{\sqrt{3}}{2} \left ( x-\frac{\pi}{6} \right ) - \frac{1}{2(2!)}\left ( x-\frac{\pi}{6} \right )^{2} - \frac{\sqrt{3}}{2(3!)} \left ( x-\frac{\pi}{6} \right )^{3}. $$ Figure 9.7.7 compares the graphs for \(f(x)=\sin x\) and \(P_{3}\).

Example 9.7.7 Approximation Using Maclaurin Polynomials

Use a fourth Maclaurin polynomial to approximate the value for \(\ln(1.1)\).
Solution Because 1.1 is closer to 1 than to 0 consider Maclaurin polynomials for the function \(g(x)=\ln(1+x)\).

\( g(x)= \ln(1+ x) \)	\( g(\color{red}{0})= \ln(1+ \color{red}{0}) = 0 \)
\( g{}^{\prime }(x)=(1+x)^{-1} \)	\( g{}^{\prime }(1+ \color{red}{0})^{-1}= 1 \)
\( g{}^{\prime \prime }(x)=-(1+x)^{-2} \)	\( g{}^{\prime \prime }(\color{red}{0})=-(1+\color{red}{0})^{-2}= -1 \)
\( g{}^{\prime \prime \prime }(x)=2(1+x)^{-3} \)	\( g{}^{\prime \prime \prime }(\color{red}{0})=2(1+\color{red}{0})^{-3}=2 \)
\( g{}^{ (4) }(x)=-6(1+x)^{-4} \)	\( g{}^{ (4) }(\color{red}{0})=-6-(1+\color{red}{0})^{-4}=-6 \)

Note that these coefficients are the same as in Example 9.7.4. Therefore, the fourth Maclaurin polynomial for \( g(x)= \ln(1+ x) \) is

$$P_{4}(x) $$	$$=g(0)+ g{}^{\prime}(0)x + \frac{g{}^{\prime \prime}(0)}{2!}x^{2}+ \frac{g{}^{\prime \prime \prime}(0)}{3!}x^{3} + \frac{g{}^{(4)}(0)}{4!}x^{4}$$
	$$=x-\frac{1}{2}x^{2}+\frac{1}{3}x^{3}-\frac{1}{4}x^{4}. $$

Consequently,

$$ \ln(1.1)= \ln(1+0.1) \approx P_{4}(0.1) \approx 0.0953083.$$

Table 9.7.2 illustrates Maclaurin polynomial approximation for \(\ln(1.1)\) to seven decimal places. As \(n\) increases, \(P_{n}(0.1)\) approaches 0.0953102.

Table 9.7.2 Maclaurin Polynomials and Approximations for \(\ln(1+x)\) at \(x=0.1\)
\(n\)	1	2	3	4
\(P_{n}(0.1)\)	0.1000000	0.0950000	0.0953333	0.0953083

Table 9.7.3 illustrates that as you move away from the expansion point \(c=0\), the approximation's accuracy decreases.

Table 9.7.3 Maclaurin Polynomials and Approximations for \(\ln(1+x)\)
\(x\)	0	1	2	3	4
\(\ln(1+x)\)	0	0.0953102	0.4054651	0.5596158	0.6931472
\(P_{4}(x)\)	0	0.0953083	0.4010417	0.5302734	0.5833333

Tables 9.7.2 and 9.7.3 illustrate two very important points about Taylor and Maclaurin polynomials accuracy for use in approximations.

1. The approximation is usually better for higher-degree Taylor or Maclaurin polynomials than for those with a lower degree.
2. The approximation is usually better at \(x\)-values close to \(c\) than at \(x\)-values far from \(c\).

Taylor Polynomial Remainder

How accurate is the Taylor approximation? Subtract the approximation from the actual value and a remainder is left over. The smaller the remainder, the more accurate the approximation. This is described in Definition 9.7.2

Definition 9.7.2 Taylor Polynomial Remainder

Let \(f(x)\) be a differentiable function and \(P_{n}(x)\) be a Taylor Approximation for \(f\). The remainder \(R_{n}(x)\) is defined as.

Table 9.7.4 Taylor Polynomial Remainder
Exact value	Taylor Approx.	Remainder
\( f(x)\)	\( = P_{n}(x) \)	\( + R_{n}(x) \)

Solving for the remainder produces \( R_{n}(x)=f(x)- P_{n}(x) \). The absolute value for \(R_{n}(x) \) is called the error associated with the approximation. As an equation,

$$ Error = |R_{n}(x)| = |f(x)-P_{n}(x)| .$$

Theorem 9.7.1 Taylor's Theorem

If \(f(x)\) is a differentiable function through order \(n+1\) over an interval \(I\) containing \(c\), the, for each \(x\) in \(I\), there exists \(z\) between \(x\) and \(c\) such that $$ f(x)=f(c)+f{}^{\prime}(c)(x-c) + \frac{f{}^{\prime \prime}(c)}{2!}(x-c)^{2}+\cdots+\frac{f{}^{(n)}(c)}{n!}(x-c)^{n}+R_{n}(x)$$ where $$R_{n}(x)= \frac{f^{n+1}(z)}{(n+1)!}(x-c)^{n+1}. $$ The remainder is called the Lagrange form for the remainder.

A useful variant on Taylor's Theorem is that

$$|R_{n}(x)| \leqslant \frac{|x-c|^{n+1}}{(n+1)!} \text{max} |f^{(n+1)}(z)| $$

where max\(|f^{(n+1)}(z)| \) is the maximum value for \(f^{(n+1)}(z)\) between \(x\) and \(c\).

When applying Taylor’s Theorem do not expect to find an exact value for \(z\). If you find \(z\), no approximation is needed. Try finding the bounds for \(f^{(n+1)}(z)\) that produces an \(R_{n}(x)\) with an acceptable size.

Example 9.7.8 Determining an Approximation's Accuracy

The third Maclaurin polynomial for \(\sin x \)is

$$P_{3}(x)=x-\frac{1}{3!}x^{3}$$

Use Taylor’s Theorem to approximate \( \sin (0.1)\) by \(P_{3}(0.1)\) and determine the approximation's accuracy.
Solution Using Taylor’s Theorem produces

$$ \sin x=x-\frac{1}{3!}x^{3}+R_{3}(x)= x-\frac{1}{3!}x^{3}+ \frac{f{}^{(4)}(z)}{4!}x^{4}$$

where \(0 < z < 0.1\). Therefore,

$$ \sin(\color{red}{0.1}) \approx \color{red}{0.1}-\frac{(\color{red}{0.1})^{3}}{3!} \approx 0.1 -0.000167 = 0.099833.$$

Because \( f{}^{(4)}(z) = \sin z\), it follows that the error \(|R_{n}(0.1)|\) can be bounded as follows.

$$0 < R_{3}(\color{red}{0.1}) = \frac{\sin z}{4!}(\color{red}{0.1})^{4} < \frac{0.0001}{4!} \approx 0.000004 $$

This implies that

$$ 0.099833 < \sin(0.1) \approx 0.099833 + R_{3}(0.1) < 0.099833 + 0.000004 $$

or

$$ 0.099833 < \sin(0.1) < 0.099837.$$

Example 9.7.9 Approximating a Value to a Desired Accuracy

Given a Taylor polynomial, \(P_{n}(x)\), expanded about \(c=1\). Determine the degree needed to approximate \(\ln(1.2)\) with an error less than 0.001.
Solution Referring to Example 9.7.4, the \((n+1)\)st derivative for \(f(x)=\ln x\) is.

$$ f{}^{(n+1)}(x)=(-1)^{n} \frac{n!}{x^{n+1}}$$

Using Taylor's Theorem, the error for \(|R_{n}(1.2)|\)is

$$|R_{n}(\color{red}{1.2})| $$	$$= \left | \frac{f{}^{(n+1)}(z)}{(n+1)!}(\color{red}{1.2}-1)^{n+1} \right | $$
	$$=\frac{n!}{z^{n+1}} \left [ \frac{1}{(n+1)!} \right ] (0.2)^{n+1} $$
	$$= \frac{(0.2)^{n+1}}{z^{n+1}(n+1)} $$

where \(1 < z < 1.2\). On this interval, \((0.2)^{n+1}/[z^{n+1}(n+1)]\) is less than \((0.2)^{n+1}/(n+1)\). The bounds for \(n\) should be such that

$$ \frac{(0.2)^{n+1}}{(n+1)}< 0.001 \rightarrow 1000 < (n+1)5^{n+1}. $$

By trial and error, you can determine that the least value for \(n\) that satisfies this inequality is \(n=3\). A third Taylor polynomial is needed to achieve the desired accuracy in approximating \(\ln(1.2)\).

Internal Links

Parent Article: Calculus II 09 Infinite Series