Calculus I 03.03 Increasing and Decreasing Functions and the First Derivative Test

Previous	Calculus I 03.02 Rolle’s Theorem and the Mean Value Theorem
Next	Calculus I 03.04 Concavity and the Second Derivative Test

3.3 Increasing and Decreasing Functions and the First Derivative Test

• Determine intervals on which a function is increasing or decreasing.
• Apply the First Derivative Test to find relative extrema.

Increasing and Decreasing Functions

Derivatives can be used to classify relative extrema as either relative minima or relative maxima. Starting with defining increasing and decreasing functions.

Definition 3.3.1 Increasing and Decreasing Functions

A function's derivative is related to it's slope. Figure 3.3.1

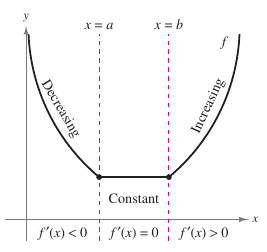
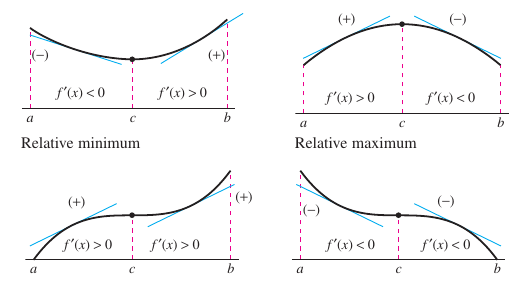
1. A function \(f\) is increasing on an interval when, for any two numbers \(x_1\) and \(x_2\) in the interval, \(x_1<x_2\) implies \(f(x_1)< f(x_2)\). 2. A function \(f\) is decreasing on an interval when, for any two numbers \(x_1\) and \(x_2\) in the interval, \(x_1<x_2\) implies \(f(x_1)> f(x_2)\). A function is increasing when, as \(x\) moves to the right, its graph moves up, and is decreasing when its graph moves down. For example, the function in Figure 3.3.1 is decreasing on the interval \((-\infty,a)\), is constant on the interval \((a,b)\), and is increasing on the interval \((b,\infty)\). As shown in Theorem 3.3.1 below, a positive derivative implies the function is increasing, a negative derivative implies the function is decreasing, and a zero derivative on an entire interval implies the function is constant on that interval. Theorem 3.3.1 Test for Increasing and Decreasing Functions Let \(f\) be a function that is continuous on the closed interval \([a,b]\) and differentiable on the open interval \((a,b)\). 1. If \({f}'(x)>0\) for all \(x\) in \((a,b)\), then \(f\) is increasing on \([a,b]\). 2. If \({f}'(x)<0\) for all \(x\) in \((a,b)\), then \(f\) is decreasing on \([a,b]\). 3. If \({f}'(x)=0\) for all \(x\) in \((a,b)\), then \(f\) is constant on \([a,b]\). Cases 1 and 2 are valid even when \({f}'(x)=0\) at a finite number of \(x\)-values in \((a,b)\). Proof Prove the first case by assuming that \({f}'(x)>0\) for all \(x\) in the interval \((a,b)\) and let \(x_1<x_2\) be any two points in the interval. By the Mean Value Theorem there exists a number \(c\) such that \(x_1<c<x_2\), and $${f}'(c)=\frac{f(x_2)-f(x-1)}{x_2-x_1}.$$ Because \({f}'(c)>0\) and \(x_2-x_1>0\), then \(f(x_2)-f(x_1) > 0\), which implies that \(f(x_1)<f(x-1)\). Therefore, \(f\) is increasing on the interval. The second and third cases have a similar proof.

Example 3.3.1 Intervals on Which \(f\) is Increasing or Decreasing

Figure 3.3.2

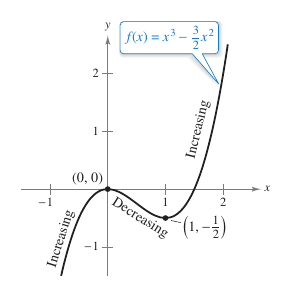
Find the open intervals on which \(f(x)=x^3-\frac{3}{2}x^2\) is increasing or decreasing. Solution Note that if \(f\) is differentiable on the entire real number line and the derivative for \(f\) is \(f(x)\) \(=x^3-\frac{3}{2}x^2\)     Original function. \({f}'(x)\) \(=3x^2-3x\)     Differentiate To determine the critical numbers for \(f\), set \({f}'(x)\) equal to zero. \(3x^2-3x\) \(=0\)     Set \({f}'(x)\) equal to zero. \(3(x)(x-1)\) \(=0\)     Factor \(x\) \(=0,\:1\)     Critical numbers Because there are no points for which \({f}'\) does not exist, the conclusion is that \(x=0\) and \(x=1\) are the only critical numbers. Table 3.3.1 summarizes the testing on three intervals determined by these two critical numbers. Table 3.3.1 Interval \(-\infty <x < 0\) \(0< x < 1\) \(1< x < \infty\) Test Value \(x=-1\) \(x=\frac{1}{2}\) \(x=2\) Sign for \({f}'(x)\) \({f}'(-1)=6>0\) \({f}'(\frac{1}{2})=-\frac{3}{4} <0\) \({f}'(2)=6>0\) Conclusion Increasing Decreasing Increasing By Theorem 3.3.1, \(f\) is increasing on the intervals \((-\infty,0)\) and \((1,\infty)\) and decreasing on the interval \((0,1)\), as shown in Figure 3.3.2.

Example 3.3.1 describes one method for finding intervals on which a function is increasing or decreasing. The guidelines below summarize the steps it followed.

Figure 3.3.3

Guidelines for Finding Intervals on Which a Function is Increasing or Decreasing Let \(f\) be continuous on the interval \((a,b)\). To find the open intervals on which \(f\) is increasing or decreasing use the following steps. 1. Locate the critical numbers for \(f\) in \((a,b)\), and use there numbers to determine test intervals. 2. Determine the sign for \({f}'(x)\) at one test value in each interval. 3. Use Theorem 3.3.1 to determine whether \(f\) is increasing or decreasing on each interval. 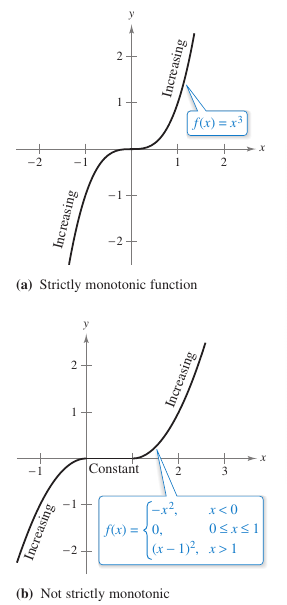These guidelines are also valid when the interval \((a,b)\) is replaced by an interval with the form \((-\infty,b)\), \((a,\infty)\), or \((-\infty,\infty)\). A function is strictly monotonic on an interval when it is either increasing on the entire interval or decreasing on the entire interval. For example, the function \(f(x)=x^3\) is strictly monotonic on the entire real number line because it is increasing on the entire real number line, as shown in Figure 3.3.3(a). The function shown in Figure 3.3,3(b) is not strictly monotonic on the entire real number line because it is constant on the interval \([0,1]\).

The First Derivative Test

Relative extrema for \(f\) Figure 3.3.4

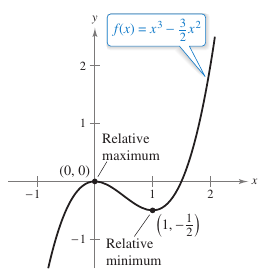
After determining the intervals on which a function is increasing or decreasing, it is not difficult to locate the relative extrema. For example, in Figure 3.3.1 the function $$f(x)=x^3-\frac{3}{2}x^2$$ has a relative maximum at the point \((0,0)\) because \(f\) is increasing immediately to the left from \(x=0\) and decreasing immediately to the right from \(x=0\). Similarly, \(f\) has a relative minimum at the point \((1,-\frac{1}{2})\) because \(f\) is decreasing immediately to the left from \(x=1\) and increasing immediately to the right from \(x=1\). The Theorem 3.3.2 formally describes this idea. Theorem 3.3.2 The First Derivative Test Let \(c\) be a critical number for a function \(f\) that is continuous on an open interval \(I\) containing \(c\). If \(f\) is differentiable on the interval, except possibly at \(c\), then \(f(c)\) can be classified as follows. 1. If \({f}'(x)\) changes from negative to positive at \(c\), then \(f\) has a relative minimum at \((c,f(c))\). 2. If \({f}'(x)\) changes from positive to negative at \(c\), then \(f\) has a relative maximum at \((c,f(c))\). 3. If \({f}'(x)\) is positive on both sides, or negative on both sides of \(c\), then \(f(c)\) is neither a relative minimum nor a relative maximum. Neither relative minimum nor relative maximum Figure 3.3.5 Proof Assume that \({f}'(x)\) changes from negative to positive at \(c\). Then there exist \(a\) and \(b\) in \(I\) such that \({f}'(x)<0\) for all \(x\) in \((a,c)\) and \({f}'(x)>0\) for all \(x\) in \((c,b)\). By Theorem 3.3.1, \(f\) is decreasing on \([a,c]\) and increasing on \([c,b]\). Therefore, \(f(c)\) is a minimum for \(f\) on the open interval \((a,b)\) and, consequently, a relative minimum for \(f\). This proves the first case. The second case is proved in a similar manner.

Example 3.3.2 Applying the First Derivative Test

A relative minimum occurs where \(f\) changes from decreasing to increasing, and a relative maximum occurs where \(f\) changes from increasing to decreasing. Figure 3.3.6

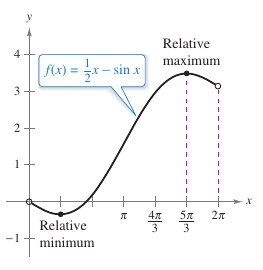
Find the relative extrema for \(f(x)=\frac{1}{2}x-\sin x\) in the interval \((0,2\pi)\). Solution Note that \(f\) is continuous on the interval \((0,2\pi)\). The derivative for \(f\) is \({f}'(x)=\frac{1}{2}- \cos x\). To determine the critical numbers for \(f\) in this interval, set \({f}'(x)\) equal to zero. $$\frac{1}{2}-\cos x$$ \(=0\)     Set \({f}'(x)\) equal to zero. $$\cos x$$ $$=\frac{1}{2}$$ \(x\) $$=\frac{\pi}{3},\:\frac{5\pi}{3}$$     Critical numbers Because there are no points for which \({f}'\) does not exist, conclude that \(x=\pi/3\) and \(x=5\pi/3\) are the only critical numbers. Table 3.3.2 summarizes testing the three intervals determined by the two critical numbers. By applying the First Derivative Test, conclude that \(f\) has a relative minimum at the point where \(x=\pi/3\) and a relative maximum at the point where \(x=5\pi/3\), as shown in Figure 3.3.6. Table 3.3.2 Interval $$0<x<\frac{\pi}{3}$$ $$\frac{\pi}{3}<x<\frac{5\pi}{3}$$ $$\frac{5\pi}{3}<x<2\pi$$ Test Value $$x=\frac{\pi}{4}$$ \(x=\pi\) $$x=\frac{7\pi}{4}$$ Sign for \({f}'(x)\) $${f}' \left ( \frac{\pi}{4} \right ) < 0$$ \({f}'(\pi)>0\) $${f}' \left ( \frac{7\pi}{4} \right ) < 0$$ Conclusion Decreasing Increasing Decreasing

Example 3.3.3 Applying the First Derivative Test

Figure 3.3.7

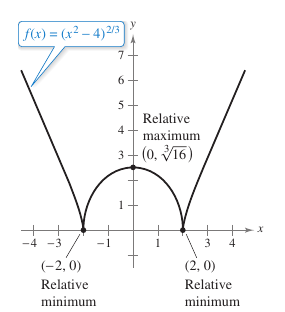
Find the relative extrema for \(f(x)=(x^2-4)^{2/3}\). Solution Begin by noting that \(f\) is continuous on the entire real number line. The derivative for \(f\) is: $${f}'(x)$$ $$=\frac{2}{3}(x^2-4)^{11/3}(2x)$$     General Power Rule $$=\frac{4x}{3}(x^2-4)^{1/3}$$     Simplify is zero when \(x=0\) and does not exist when \(x=\pm2\). Therefore, the critical numbers are \(x=-2\), \(x=0\), and \(x=2\). Table 3.3.3 summarizes testing four intervals determined by these three critical numbers. By applying the First Derivative Test, conclude that \(f\) has a relative minimum at the point \((-2,0)\), a relative maximum at the point \((0,\sqrt[3]{16})\), and another relative minimum at the point \((2,0)\), as shown in Figure 3.3.7. Table 3.3.3 Interval \(-\infty < x < -2\) \(-2<x<0\) \(0<x<2\) \(2<x<\infty\) Test Value \(x=-3\) \(x=-1\) \(x=1\) \(x=3\) Sign for \({f}'(x)\) \({f}'(-3)<0\) \({f}'(-1)>0\) \({f}'(1)<0\) \({f}'(3)>0\) Conclusion Decreasing Increasing Decreasing Increasing

Note that in Examples 3.3.1 and 3.3.2, the given functions are differentiable on the entire real number line. For such functions, the only critical numbers are those for which \({f}'(x)=0\). Example 3.3.3 concerns a function that has critical numbers in two types —those for which \({f}'(x)=0\) and those for which \(f\) is not differentiable.

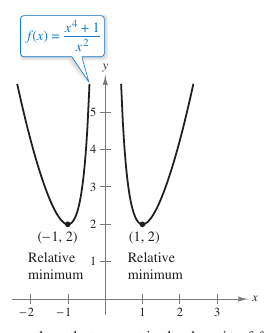
When using the First Derivative Test, be sure to consider the domain for the function. For instance, in the Example 3.3.4, the function d::$${f}'(x)=\frac{x^4-1}{x^2}$$ is not defined when \(x=0\). This \(x\)-value must be used with the critical numbers to determine the test intervals.

Example 3.3.4 Applying the First Derivative Test

\(x\)-values that are not in the domain for \(f\), as well as critical numbers, determine test intervals for \({f}'\). Figure 3.3.8

Find the relative extrema for $$f(x)=\frac{x^4+1}{x^2}$$ Solution Note that \(f\) is not defined when \(x=0\). $$f(x)$$ \(=x^2+x^{-2}\) \({f}'(x)\) \(=2x-2x^{-3}\)     Differentiate $$=2x-\frac{2}{x^3}$$     Rewrite with positive exponent. $$=\frac{2(x^4-1)}{x^3}$$     Simplify $$=\frac{2(x^2+1)(x-1)(x+1)}{x^3}$$     Factor Therefore, \({f}'(x)\) is zero at \(x=\pm 1\). Because \(x=0\) is not in the domain for \(f\), use this \(x\)-value along with the critical numbers to determine the test intervals. \(x\) \(=\pm 1\)     Critical numbers, \({f}'(\pm 1)=0\) \(x\) \(=0\)     Zero is not in the domain for \(f\) Table 3.3.4 summarizes the testing the four intervals determined by these three \(x\)-values. By applying the First Derivative Test, conclude that \(f\) has one relative minimum at the point \((-1,2)\) and another at the point \((1,2)\) as shown in Figure 3.3.8. Table 3.3.4 Interval \(-\infty < x < -1\) \(-1<x<0\) \(0<x<1\) \(0<x<1\) Test Value \(x=-2\) \(x=-\frac{1}{2}\) \(x=\frac{1}{2}\) \(x=2\) Sign for \({f}'(x)\) \({f}'(-2)<0\) \({f}'(-\frac{1}{2})>0\) \({f}'(\frac{1}{2})<0\) \({f}'(2)>0\) Conclusion Decreasing Increasing Decreasing Increasing

Example 3.3.5 Projectile Path

Projectile path with initial angle \(\theta\) Figure 3.3.9

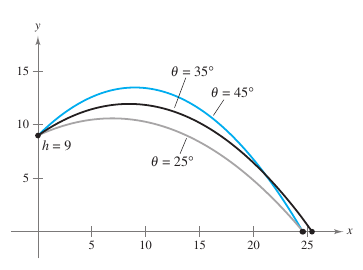
Neglecting air resistance, the projectile path propelled at an angle \(\theta\) is $$y=\frac{g \sec^2 \theta}{2v^2_0}x^2+ (\tan \theta)x+h, \:\:\:\: 0 \leq \theta \leq \frac{\pi}{2}$$ where \(y\) is the height, \(x\) is the horizontal distance, \(g\) is the acceleration due to gravity \(v_0\) is the initial velocity, and \(h\) is the initial height. This equation is derived in Section 12.3. Let \(g=-32\) feet per second per second , \(v_0=24\) feet per second, and \(h=9\) feet. What value for \(\theta\) will produce the maximum horizontal distance? Solution To find the distance the projectile travels substitute the given variables into the equation. $$y$$ $$=\frac{g \sec^2 \theta}{2v^2_0}x^2+ (\tan \theta)x+h$$ $$\color{red}{0}$$ $$=\frac{ \color{red}{-32} \sec^2 \theta}{2(\color{red}{24}^2)}x^2+(\tan \theta)x+\color{red}{9}$$ $$0$$ $$=-\frac{\sec^2 \theta}{36}x^2+(\tan \theta)+9$$ Then solve for \(x\) using the Quadratic Formula with \(a=-\sec^2 \theta/36,\: b= \tan \theta\), and \(c=9\). $$x$$ $$=\frac{-b \pm \sqrt{ b^2-4ac}}{2a}$$ $$x$$ $$=\frac{-\tan \theta \pm \sqrt{(\tan \theta)^2 -4(-\sec^2 \theta /36)(9)}}{2(-\sec^2 \theta /36)}$$ $$x$$ $$=\frac{-\tan \theta \pm \sqrt{\tan^2 \theta + \sec^2 \theta}}{-\sec^2 \theta /18}$$ \(x\) \(=18 \cos \theta(\sin \theta + \sqrt{\sin^2 \theta+1}), \:\: x \leq 0\) Next find the value for \(\theta\) that produces a maximum value for \(x\). Applying the First Derivative Test by hand would be very long and tedious. Use a computer to solve the equation \(dx/d\theta=0\), however, eliminates the most messy computations. The result is that the maximum value for \(x\) occurs when \(\theta \approx 0.61548\) radian, or 35.3°. This conclusion is reinforced by sketching the projectile path for different values for \(\theta\), as shown in Figure 3.3.9. Among the three paths shown, note that the distance traveled is greatest for \(\theta = 35\)°.

Internal Links

Parent Article: Calculus I 03 Differentiation Applications