Calculus I 03.08 Newton’s Method
| Previous | Calculus I 03.07 Optimization Problems |
| Next | Calculus I 03.09 Differentials |
Contents
3.8 Newton's Method[1]
- Approximate a function's zero using Newton’s Method.
 The \(x\)-intercept for the tangent line approximates the zero for \(f\). Figure 3.8.1 |
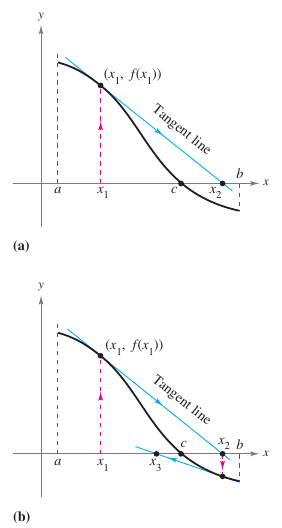
Newton's Method approximates the real zeros for a function by using tangent lines on the function's graph near the \(x\)-intercepts. Consider a function \(f\) that is continuous on the interval \([a,b]\) and differentiable on the interval \((a,b)\). If \(f(a)\) and \(f(b)\) differ in sign, then, by the Intermediate Value Theorem, \(f\) must have at least one zero on the interval \((a,b)\). A first choice for the estimate might be,
as shown in Figure 3.8.1(a). Newton’s Method assumes the graph for \(f\) and the tangent line at \((x_1,f(x))\) both cross the \(x\)-axis at about the same point. The \(x\)-intercept for this tangent line is easily calculable for this tangent line and is used as a second, and usually better, estimate for \(f\)'s zero. The tangent line passes through the point \((x_1,f(x_1))\) with a slope \({f}'(x_1)\). The equation for the tangent line in point-slope form is
Let \(y=0\) and solving for \(x\) produces
From the initial estimate for \(x_1\) obtain the new estimate is
Now improve on \(x_2\) and calculate a third estimate
Newton's Method repeatedly applies this until an estimate with the desired accuracy is produced. |
Newton's Method for Approximating the Zeros for a Function
Let \(f(c)=0\), where \(f\) is differentiable on an open interval containing \(c\). Approximate \(c\) using these steps.
1. Make an initial estimate for \(x_1\), using a graph, that is close to \(c\).
2. Determine a new approximation
- $$x_{n=1}=x_n-\frac{f(x_n)}{{f}'(x_n)}.$$
3. When \(|x_n-x_{n-1}|\) is within the desired accuracy, let \(x_{n+1}\) serve as the final approximation. Otherwise, return to Step 2 and repeat.
Each cycle through steps 1 and 2 is called an iteration.
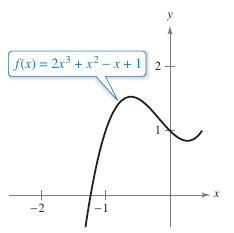
Example 3.8.1 Using Newton's Method
 Figure 3.8.2 |
Using Newton's Method calculate three iterations to approximate the zeros for
Use \(x_1=1\) as the initial guess.
The calculations for three iterations are shown in Table 3.8.1 below.
The two zeros for the function are \(\pm \sqrt{2}\). To six decimal places, \(\sqrt{2}=1.414214\). After only three iterations Newton's Method produced an approximation withing 0.000002 from an actual root. This first iteration is shown in Figure 3.8.2.  | ||||||||||||||||||||||||||||||||||||
Example 3.8.2 Using Newton's Method
 After three Newton's Method iterations the zero for \(f\) is approximated to the desired accuracy. Figure 3.8.3 |
Use Newton's Method to approximate the zeros for
Continue the iterations until two successive approximations differ by less than 0.0001.
The calculations are shown in Table 3.8.2 below.
Because two successive approximations differ by less than the required 0.0001, the estimated zero for \(f\) is -1.23375. | ||||||||||||||||||||||||||||||||||||
 Newton's Method fails to converge when \({f}'(x_n)=0\). Figure 3.8.4 |
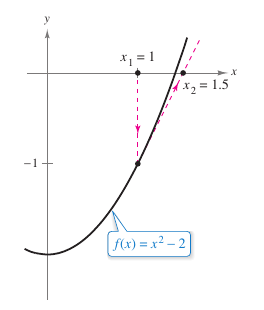
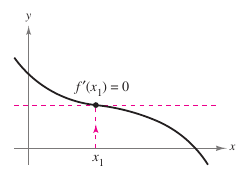
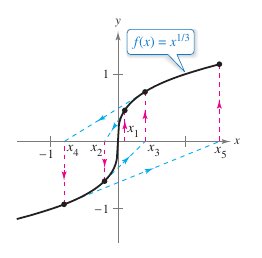
When the approximations approach a limit, the sequence \(x_1,x_2,x_3,...,x_n,...\) is said to converge, as in Examples 3.8.1 and 3.8.2. When the limit is \(c\), it can be proven that \(c\) must be a zero for \(f\). Newton’s Method does not always yield a convergent sequence, as shown in Figure 3.8.4. Because Newton’s Method involves division by \({f}'(x_n)\), the method will fail when the derivative is zero for any \(x_n\) in the sequence. This problem can be overcome it by choosing a different value for \(x_1\). Another way Newton’s Method can fail is shown in Example 3.8.3. |
Example 3.8.3 Where Newton's Method Fails
 Figure 3.8.5 |
The function
is not differentiable at \(x=0\). Show that Newton's Method fails to converge using \(x_1=0.1\).
the iterative formula is
Figure 3.8.5 shows that as \(x_n\) continues to increase in magnitude as \(n \to \infty\). Therefore the sequence's limit does not exist. The calculations are shown in Table 3.8.3 below.
Because two successive approximations differ by less than the required 0.0001, the estimated zero for \(f\) is -1.23375. | ||||||||||||||||||||||||||||||||||||
Newton's Method will always produce convergence if
|
Condition for convergence |
on an open interval containing the zero. In Example 3.8.1, this test would yield
- \(f(x)=x^2-2, \: {f}'(x)=2x, \: {f}''(x)=2\),
and
- $$ \left | \frac{f(x){f}''(x)}{[{f}'(x)]^2} \right | = \left | \frac{(x^2-2)(2)}{4x^2} \right |= \left | \frac{1}{2}-\frac{1}{x^2} \right |.$$
By Example 3.8.1.
On the interval \((1,3)\), this quantity is less than 1 and therefore the convergence is guaranteed. But in Example 3.8.3 there is
- $$f(x)=x^{1/3}, \: {f}'(x)=\frac{1}{3}x^{-2/3}, \: {f}''(x)=-\frac{2}{9}x^{-5/3}$$
and
- $$ \left | \frac{f(x){f}''(x)}{[{f}'(x)]^2} \right | = \left | \frac{x^{1/3}(-2/9)(x^{-5/3}}{(1/9)(x^{-4/3})} \right |= 2$$
which is not less than 1 for any \(x\)-values. The conclusion is that Newton's Method will converge.
Internal Links
Parent Article: Calculus I 03 Differentiation Applications
