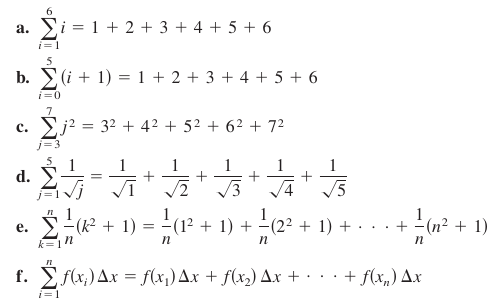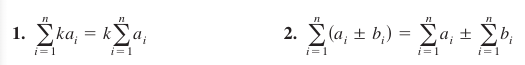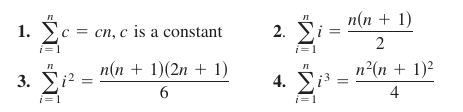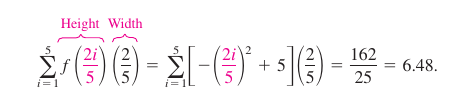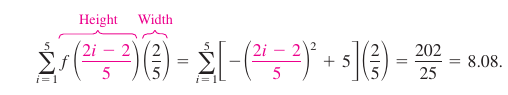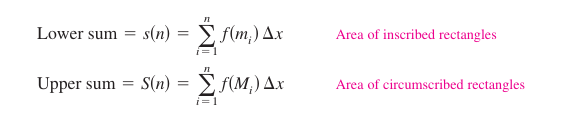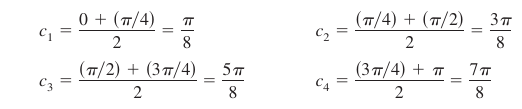Calculus I 04.02 Area

Previous	Calculus I 04.01 Antiderivatives and Indefinite Integration
Next	Calculus I 04.03 Riemann Sums and Definite Integrals

4.2 Area

• Use sigma notation to write and evaluate a sum.
• Understand what area means.
• Approximate the area for a plane region.
• Find the area for a plane region using limits.

Sigma Notation

Sigma Notation is a concise notation for sums. This notation is called sigma notation because it uses the uppercase Greek letter sigma, written as \(\Sigma\).

Definition 4.2.1 Sigma Notation

The sum for \(n\) in terms \(a_1,\:a_2,\:a_3,...,\:a_n\) is written as

$$ \sum_{i=1}^{n}a_i=a_1+a_2+a_3+\cdot\cdot\cdot+a_n$$

where \(i\) is the summation index, \(a_i\) is the \(i\)th term in the sum, and the upper and lower bounds for summation are \(n\) and 1.

The upper and lower bounds must be constant with respect to the summation index However, the lower bound doesn’t have to be 1. Any integer less than or equal to the upper bound is legitimate.

Example 4.2.1 Sigma Notation Examples

From parts (a) and (b), notice that the same sum can be represented in different ways using sigma notation.

Although any variable can be used as the summation index, \(i\), \(j\), and \(k\) are often used. Notice in Example 4.2.1 that the summation index does not appear in the expanded sum's terms.

The summation properties shown Theorem 4.2.1 can be derived using the Addition's Associative and Commutative Properties and the Distributive Property of Addition over Multiplication. In the first property, \(k\) is a constant, not an index.

Theorem 4.2.1 Summation Formulas

Example 4.2.2 Evaluating a Sum

Evaluate

$$\sum_{i=1}^{n} \frac{i+1}{n^2}$$

for \(n=10,\:100,\:1000,\:\text{ and } \: 10,000.\)
Solution

$$\sum_{i=1}^{n} \frac{i+1}{n^2}$$	$$=\frac{1}{n^2} \sum_{i=1}^{n}(i+1)$$	Factor the constant \(1/n^2\) from the sum
	$$==\frac{1}{n^2} \left ( \sum_{i=1}^{n} i + \sum_{i=1}^{n} 1 \right )$$	Write as two sums
	$$=\frac{1}{n^2} \left [ \frac{n(n+1)}{2} + n \right ]$$	Apply Theorem 4.2.1
	$$=\frac{1}{n^2} \left [ \frac{n^2+3n}{2} \right ]$$	Simplify
	$$= \frac{n+3}{2n} $$	Simplify

Evaluate the sum by substituting the appropriate \(n\)-values, as shown in Table 4.2.1.

Table 4.2.1
\(n\)	10	100	1000	10,000
$$\sum_{i=1}^{n} \frac{i+1}{n^2}= \frac{n+3}{2n}$$	0.65000	0.51500	0.50150	0.50015

In Table 4.2.1, note that the sum appears to approach a limit as \(n\) increases. Although limits at infinity applies to a variable \(x\), where \(x\) is any real number, many results hold true for limits involving the variable \(n\), where \(n\) is restricted to positive integer values. To find the limit for \((n+3)/2n\) as \(n\) approaches infinity the expression can be written as

$$ \lim_{n \to \infty} \frac{n+3}{2n}=\lim_{n \to \infty} \left ( \frac{n}{2n} +\frac{3}{2n} \right )=\lim_{n \to \infty} \left ( \frac{1}{2} +\frac{3}{2} \right ) = \frac{1}{2}+\frac{3}{2}=2.$$

Area

Triangle: \(A=1/2\: bh\) Figure 4.2.1

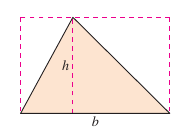
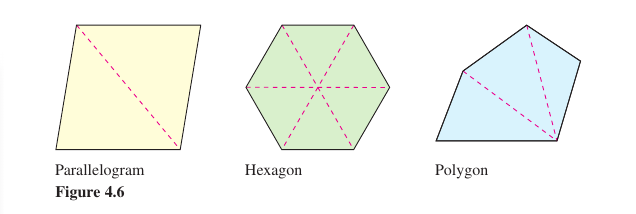
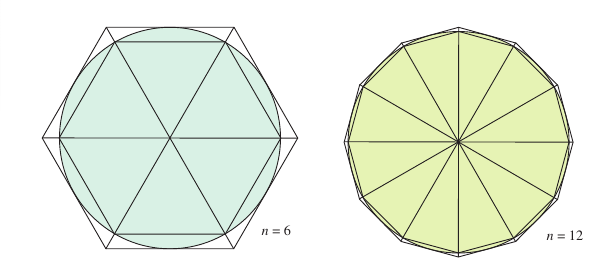
In Euclidean geometry, the simplest plane region is a rectangle. Although people often say that the formula for the area of a rectangle is \(A=bh\) it is actually more proper to day that this is the definition for a rectangle's area. From this definition many formulas for plane regions are derived. For example, to determine a triangle's area, form a rectangle whose area is twice the triangle's, as shown in Figure 4.2.1. Then the area for any polygon can be determined by subdividing it into triangular regions, as shown in Figure 4.2.2. Figure 4.2.2 Finding the areas for regions other than polygons is more difficult. The ancient Greeks were able to determine area formulas for some general 2D and 3D shapes, principally bounded by conics, by the exhaustion method. That is, by calculating the area for each triangle by hand on paper and then verified by another mathematician. The clearest description for this method was given by Archimedes. For example, in Figure 4.2.3, the area for a circular region is approximated by an \(n\)-sided inscribed polygon and an \(n\)-sided circumscribed polygon. For each \(n\)-value, the area for the inscribed polygon is less than the area for the circle, and the area for the circumscribed polygon is greater than the area for the circle. Moreover, as \(n\) increases, the areas for both polygons become better and better approximations for the circle's area. The exhaustion method for finding the area for a circular region Figure 4.2.3 A similar process was used by Archimedes to determine the area for a plane region is used in the remaining examples in this section.

The Area for a Plane Region

Calculus' origins are connected to two classic problems: the tangent line problem and the area problem. Example 4.2.3 begins the investigation into the area problem.

Example 4.2.3 Approximating the are for a Plane Region

Figure 4.2.3

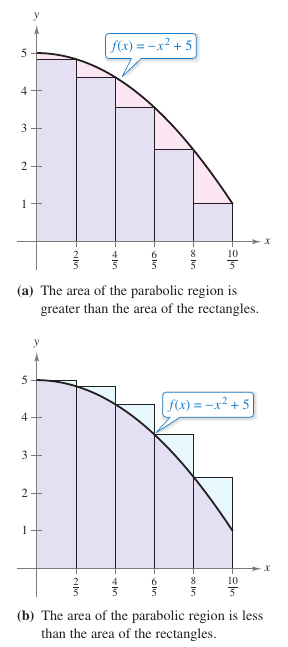
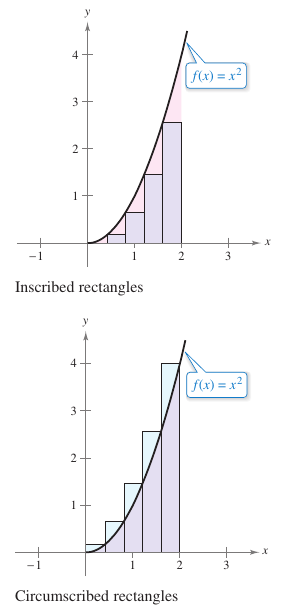
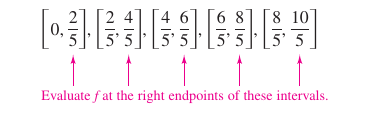
Using the five rectangles in Figure 4.2.3(a) and (b) to find two approximations for the region's area lying between the graph for \(f(x)=-x^2+5\) and the \(x\)-axis between \(x=0\) and \(x=2.\) Solution a. The right endpoints for the five intervals are $$\frac{2}{5}i$$     Right endpoints where \(i=1,\:2,\:3,\:4,\:5.\) The width for each rectangle is \(\frac{2}{5}\), and the height for each rectangle can be obtained by evaluating \(f\) at the right endpoint for each interval. The five rectangles' area are summed below Because each triangle lies inside the parabolic region, the conclusion is the area for the parabolic region is greater than 6.48. b. The left endpoints for the five intervals are $$\frac{2}{5}(i-1)$$     Left endpoints where \(i=1,\:2,\:3,\:4,\:5.\) The width for each rectangle is \(\frac{2}{5}\), and the height for each rectangle can be obtained by evaluating \(f\) at the left endpoint for each interval. The sum is Because the parabolic region lies with the union among the five rectangular regions, conclude the area for the parabolic region is less than 8.08. By combining the results for parts (a) and (b), the conclusion is 6.48 < (Area for region) < 8.08.

Upper and Lower Sums

The region under a curve Figure 4.2.4 The interval \([a,b]\) is divided into subinterval with width \(\Delta x=\frac{b-a}{n}.\) Figure 4.2.5

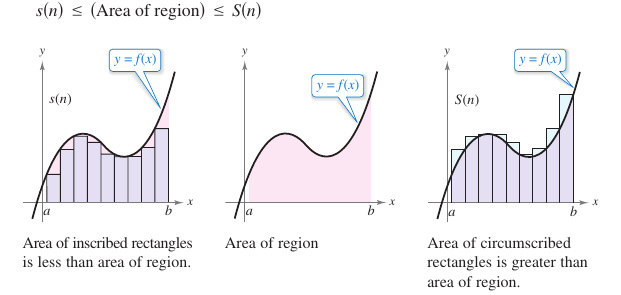
The procedure used in Example 4.2.3 can be generalized as follows. Consider a plane region bounded above by the graph for a nonnegative, differentiable, continuous function \(y=f(x)\) as shown in Figure 4.2.4. The region is bounded below by the \(x\)-axis, and on the left and right are the vertical lines \(x=a\) and \(x=b.\) To approximate the region's area, begin by subdividing the interval \([a,b]\) into \(n\) subintervals, each $$\Delta x = \frac{b-a}{n}$$ wide, as shown in Figure 4.2.5. The endpoints for the intervals are $$\color{red}{\overbrace{\color{black}{a+0(\Delta x)}}^{\color{red}{\text{a=x_0}}}}<\color{red}{\overbrace{\color{black}{a+1(\Delta x)}}^{\color{red}{\text{a=x_1}}}}<\color{red}{\overbrace{\color{black}{a+2(\Delta x)}}^{\color{red}{\text{a=x_2}}}}<\cdot \cdot \cdot <\color{red}{\overbrace{\color{black}{a+n(\Delta x)}}^{\color{red}{\text{x_n=b}}}}$$ Because \(f\) is continuous, the Extreme Value Theorem guarantees a minimum and maximum values for \(f(x)\) existences in each subinterval. 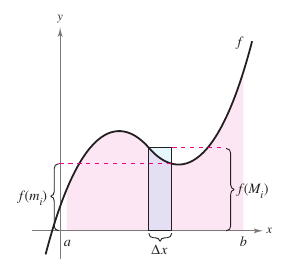\(f(m_i)=\) Minimum value for \(f(x)\) in the \(i\)th subinterval \(f(M_i)=\) Maximum value for \(f(x)\) in the \(i\)th subinterval Next, define an inscribed rectangle lying inside the \(i\)th subregion and a circumscribed rectangle extending outside the \(i\)th subregion. The height for the \(i\)th inscribed rectangle is \(f(m_i)\) and the height for the \(i\)th circumscribed rectangle is \(f(M_i\). For each \(i\), the area for the inscribed rectangle is less than or equal to the area for the circumscribed rectangle. $$\left ( \frac{\text{Inscribed area}}{\text{rectangle}} \right ) = f(m_i) \Delta x \leq f(M_i) \Delta x=\left ( \frac{\text{Cirumscribed area}}{\text{rectangle}} \right )$$ Sum the inscribed rectangles areas, called an lower sum. Sum the circumscribed rectangles areas, called an upper sum. The lower sum \(s(n)\) is less than or equal to the upper sum \(S(n)\), as shown in Figure 4.2.6. The actual area for the region lies between the sums. Figure 4.2.6

Example 4.2.4 Finding Upper and Lower Sums for a Region

Figure 4.2.7

Find the upper and lower sums for the region bounded by the graph for \(f(x)=x^2\) and the \(x\)-axis between \(x=0\) and \(x=2\). Solution Begin by partitioning the interval \([0,2]\) into \(n\) subintervals , each $$\Delta x=\frac{b-a}{n}=\frac{2-0}{n}=\frac{2}{n}$$ wide. The endpoints for each subinterval and inscribed rectangle is shown in Figure 4.2.7. Because \(f\) is increasing on the interval \([0,2]\), the minimum value on each subinterval occurs at the left endpoint and the maximum value occurs at the right endpoint. Left Endpoints Right Endpoints $$m_i=0+(i-1)\left ( \frac{2}{n} \right ) = \frac{2(i-1)}{n}$$ $$M_i=0+i)\left ( \frac{2}{n} \right ) = \frac{2i}{n}$$ Using the left endpoints, the lower sum is \(s(n)\) $$=\sum_{i=1}^{n}f(m_i)\Delta x$$ $$=\sum_{i=1}^{n} \left [ \frac{2(i-1)}{n} \right ] \left ( \frac{2}{n} \right )$$ $$=\sum_{i=1}^{n} \left [ \frac{2(i-1)}{n} \right ]^2 \left ( \frac{2}{n} \right )$$ $$=\sum_{i=1}^{n} \left ( \frac{8}{n^3} \right ) (i^2-2i+1)$$ $$=\frac{8}{n^3} \left ( \sum_{i=1}^{n}i^2-2\sum_{i=1}^{n}i+\sum_{i=1}^{n}1 \right )$$ $$=\frac{8}{n^3} \left \{ \frac{n(n+1)(2n+1)}{6}-2 \left [ \frac{n(n+1)}{2} \right ] +n \right \}$$ $$=\frac{4}{3n^3}(2n^3-3n^2+n)$$ $$=\frac{8}{3}- \frac{4}{n} + \frac{4}{3n^2}$$     Lower sum Using the right endpoints, the upper sum is \(S(n)\) $$=\sum_{i=1}^{n}f(M_i)\Delta x$$ $$=\sum_{i=1}^{n} f\left ( \frac{2i}{n} \right )^2 \left ( \frac{2}{n} \right )$$ $$=\sum_{i=1}^{n} \left ( \frac{8}{n^3} \right )i^2 $$ $$= \frac{8}{n^3} \left [ \frac{n(n+1)(2n+1)}{6} \right ]$$ $$=\frac{4}{3n^3} (2n^3+3n^2+n)$$ $$=\frac{8}{3}- \frac{4}{n} + \frac{4}{3n^2}$$     Upper sum

Example 4.2.4 illustrates some important properties about lower and upper sums. First, notice that for any \(n\)-values, the lower sum is less than, or equal to, the upper sum.

$$s(n)=\frac{8}{3}-\frac{4}{n}+\frac{4}{3n^2} < \frac{8}{3}-\frac{4}{n}+\frac{4}{3n^2}=S(n)$$

Second, the difference between the sums lessens as \(n\) increases. Taking the limits as \(n \to \infty\), both the lower and upper sums approach \(\frac{8}{3}\).

$$\lim_{n \to \infty } s(n)=\lim_{n \to \infty } \left ( \frac{8}{3}-\frac{4}{n}+\frac{4}{3n^2} \right )=\frac{8}{3}$$

Lower sum limit

and

$$\lim_{n \to \infty } S(n)=\lim_{n \to \infty } \left ( \frac{8}{3}-\frac{4}{n}+\frac{4}{3n^2} \right )=\frac{8}{3}$$

Upper sum limit

Theorem 4.4.2 shows the limits converge, as \(n \to \infty\), is no mere coincidence. This is true for all functions that are continuous and non-negative on the closed interval. The proof of this theorem is best left to a course in advanced calculus.

Theorem 4.2.2 Limits for the Lower and Upper Sums

Let \(f\) be continuous and non-negative on the interval \([a,b]\). The limits as \(n \to \infty\) for both sums exist and are equal to each other.
That is,

$$\lim_{n \to \infty } s(n)$$	$$=\lim_{n \to \infty } \sum_{i=1}^{n} f(m_i) \Delta x$$
	$$=\lim_{n \to \infty } \sum_{i=1}^{n} f(M_i) \Delta x$$
	$$=\lim_{n \to \infty } S(n)$$

where \(\Delta x = (b-a)/n\) and \(f(m_i)\) and \(f(M_i\) are the maximum and minimum values for \(f\) on the sub-interval.

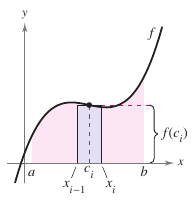
In Theorem 4.2.2, the same limit is attained for both the minimum value \(f(m_i)\) and the maximum value \(f(M_i)\). It follows from Theorem 1.3.8, The Squeeze Theorem, that the choice for \(x\) in the \(i\)th sub-interval does not affect the limit. This means any arbitrary \(x\)-value in the\(i\)th sub-interval can be chosen, as shown Definition 4.2.2.

Definition 4.2.2 Area for a Region on a Plane

The width for the \(i\)th subinterval is \(\Delta x=x_i-x_{i-1}\). Figure 4.2.8

Let \(f\) be continuous and nonnegative on the interval \([a,b]\), as shown in Figure 4.2.8. The area for the region bounded by the graph for \(f\), the \(x\)-axis, and the vertical lines \(x=a\) and \(x=b\) is $$\text{Area}=\lim_{n \to \infty } \sum_{i=1}^{n} f(c_i) \Delta x$$ where \(x_{i-1} \leq c_i \leq x_i\) and $$\Delta x= \frac{b-a}{n}.$$

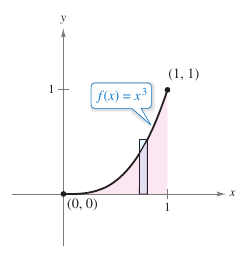
Example 4.2.5 Finding Area by the Limit Definition on an Increasing Function

Figure 4.2.9

Find the area for the region bounded by the graph for \(f(x)=x^3\), the \(x\)-axis, and the vertical lines \(x=0\) and \(x=1\), as shown in Figure 4.2.9. Solution Begin by noting that \(f\) is continuous and nonnegative on the interval \([0,1]\). Then partition the interval into \(n\) subintervals, each $$\Delta x=\frac{1}{n}$$ wide. According to Definition 4.2.2, any \(x\)-value in the \(i\)th subinterval can be chosen. For this example, the right endpoints $$c_i=\frac{i}{n}$$ are convenient. $$\text{ Area }$$ $$=\lim_{n \to \infty } \sum_{i=1}^{n} f(c_i) \Delta x$$ $$=\lim_{n \to \infty } \sum_{i=1}^{n} \left ( \frac{i}{n} \right )^3 \left ( \frac{1}{n} \right )$$     Right endpoints \(c_i=\frac{i}{n}\) $$=\lim_{n \to \infty } \frac{1}{n^4} \left [ \frac{n^2(+1)^2}{4} \right ]$$ $$=\lim_{n \to \infty } \left ( \frac{1}{4} + \frac{1}{2n}+ \frac{1}{4n^2} \right )$$ $$=\frac{1}{4}$$ The area for the region is \(\frac{1}{4}.\)

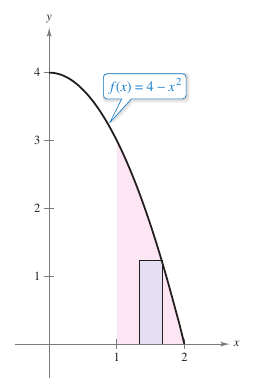
Example 4.2.6 Finding Area by the Limit Definition on a Decreasing Function

Figure 4.2.10

Find the area for the region bounded by the graph for \(f(x)=4-x^2\), the \(x\)-axis, and the vertical lines \(x=1\) and \(x=2\), as shown in Figure 4.2.10. Solution Note the function \(f\) is continuous and nonnegative on the interval \([1,2]\). Begin by partitioning the interval into \(n\) subintervals, each $$\Delta x=\frac{1}{n}$$ wide. Choosing the right endpoint $$c_i=a + i\Delta x = 1 + \frac{i}{n}$$     Right endpoints $$\text{ Area }$$ $$=\lim_{n \to \infty } \sum_{i=1}^{n} f(c_i) \Delta x$$ $$=\lim_{n \to \infty } \sum_{i=1}^{n} \left [4 - \left ( 1+ \frac{i}{n} \right )^2 \right ] \left ( \frac{1}{n} \right )$$ $$=\lim_{n \to \infty } \sum_{i=1}^{n} \left ( 3- \frac{2i}{n} - \frac{i^2}{n^2} \right ) \left ( \frac{1}{n} \right )$$ $$=\lim_{n \to \infty } \left ( \frac{1}{n} \sum_{i=1}^{n}3 - \frac{2}{n^2}\sum_{i=1}^{n}i-- \frac{1}{n^3}\sum_{i=1}^{n} i^2 \right )$$ $$=\lim_{n \to \infty } \left [ 3- \left ( 1+ \frac{1}{n} \right ) - \left ( \frac{1}{3} +\frac{1}{2n}+\frac{1}{6n^2} \right ) \right ]$$ $$=3-1-\frac{1}{3}$$ $$=\frac{5}{3}$$ The area for the region is \(\frac{5}{3}.\)

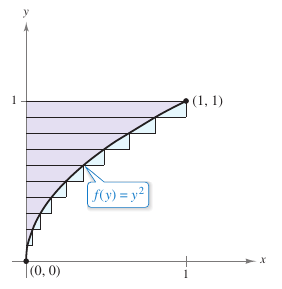
Example 4.2.7 A Region Bounded by the \(y\)-axis

Figure 4.2.11

Find the area for the region bounded by the graph for \(f(y)=y^2\), the \(y\)-axis for \(0 \leq y \leq 1\), as shown in Figure 4.2.11. \([0,1]\). Solution Begin by partitioning the interval \([0,1]\) into \(n\) subintervals, each $$\Delta y=\frac{1}{n}$$ wide. Using the upper endpoints $$c_i=\frac{1}{n},$$ produces $$\text{ Area }$$ $$=\lim_{n \to \infty } \sum_{i=1}^{n} f(c_i) \Delta y$$ $$=\lim_{n \to \infty } \sum_{i=1}^{n} \left (\frac{i}{n} \right )^2 \left ( \frac{1}{n} \right )$$     Upper endpoints $$=\lim_{n \to \infty } \frac{1}{n^3} \sum_{i=1}^{n} i^2$$ $$=\lim_{n \to \infty } \frac{1}{n^3} \left [ \frac{n(n+1)(2n+1)}{6} \right ]$$ $$=\lim_{n \to \infty } \left ( \frac{1}{3} + \frac{1}{2n} + \frac{1}{6n^2} \right ) $$ $$=\frac{1}{3}.$$ The area for the region is \(\frac{1}{3}.\)

In Examples 4.2.5, 4.2.6, and 4.3.27, \(c_i\) is a convenient value for calculating the limit. Because each limit gives the exact area for any \(c_i\), there is no need to find values that give a good approximations when \(n\) is small. For a better approximation find a value for \(c_i\) that gives a good approximation for the area on the \(i\)th subregion. In general, a good value to choose is the midpoint for the interval and apply the Midpoint Rule.

$$\text{ Area } \approx \sum_{i=1}^{n} f \left ( \frac{x_i+x_{i-1}}{2} \right ) \Delta x$$

Midpoint Rule

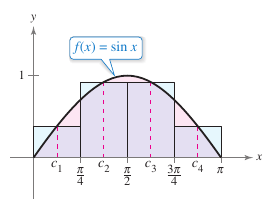
Example 4.2.8 Approximating Area with the Midpoint Rule

Figure 4.2.12

Use the Midpoint Rule with \(n=4\) to approximate the area for the region bounded by the graph for \(f(x)=\sin x\) and the \(x\)-axis for \(0 \leq x \leq \pi\), as shown in Figure 4.2.12. Solution For \(n=4\), \(\Delta x=\pi/4\). The midpoints for the subregions are shown below. $$\text{ Area } \approx \sum_{i=1}^{n} f(c_i) \Delta x=\sum_{i=1}^{4}(\sin c_i)\left ( \frac{\pi}{4} \right ) = \frac{\pi}{4} \left ( \sin \frac{\pi}{8} + \sin \frac{3\pi}{8}+\sin \frac{5\pi}{8} + \sin \frac{7\pi}{8} \right ) $$ which is about 2.052.

Internal Links

Parent Article: Calculus I 04 Integration