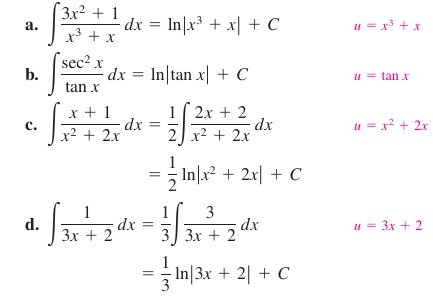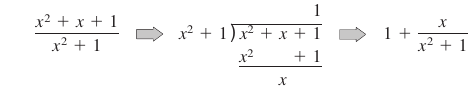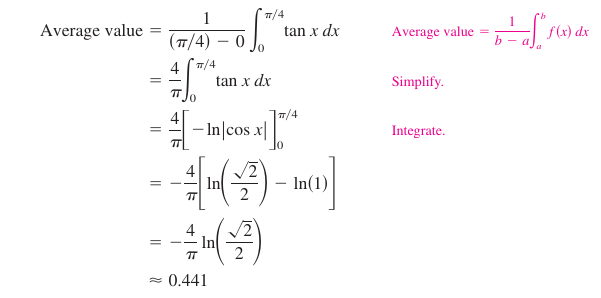Calculus I 05.02 The Natural Logarithmic Function: Integration

Previous	Calculus I 05.01 The Natural Logarithmic Function: Differentiation
Next	Calculus I 05.03 Inverse Functions

5.2 The Natural Logarithmic Function: Integration

• Integrate a rational function with the Log Rule.
• Integrate trigonometric functions.

Log Rule for Integration

The differentiation rules

$$\frac{d}{dx} [ \ln \left | x \right | ] =\frac{1}{x}\:\:\:\:\text{and}\:\:\:\:\frac{d}{dx} [ \ln \left | u \right | ] =\frac{{u}'}{u}$$

discussed in Section 5.1 produces Theorem 5.2.1.

Theorem 5.2.1 Log Rule for Integration

Let \(u\) be a differentiable function for \(x\).

$$\textbf{1.}\:\:\int \frac{1}{x}\:dx= \ln \left | x \right |+C\:\:\:\:\textbf{2.}\:\:\int \frac{1}{u}\:du= \ln \left | u \right |+C$$

Because \(du = {u}'\:dx\), the second part can also be written as

$$\int \frac{{u}'}{u}\:dx = \ln \left | u \right |+C.\:\:\:\:\color{red}{\text{Log Rule Part 2, alternative form.}}$$

Example 5.2.1 Using the Log Rule for Integration

$$\int \frac{2}{x}\:dx$$	$$=2 \int \frac{1}{x}\:dx$$	Constant Multiple Rule
	\(= 2 \ln \left | x \right |+C\)	Log Rule for Integration
	\(= \ln (x^2)+C\)	Logarithm property

Because \(x^2\) cannot be negative, the absolute value notation is unnecessary in the final antiderivative form.

Example 5.2.2 Using the Log Rule with Variable Change

Find

$$\int \frac{1}{4x-1}\: dx.$$

Solution Let \(u=4x-1\), then \(du= 4x\:dx\).

$$\int \frac{1}{4x-1}\: dx$$	$$=\frac{1}{4} \int \left ( \frac{1}{4x-1} \right ) 4\:dx$$	Multiply and divide by 4.
	$$= \frac{1}{4} \int \frac{1}{\color{red}{u}}\:du$$	Substitute: \(u=4x-1\)
	$$= \frac{1}{4} \ln \left | u \right | +C$$	Apply Log Rule
	$$= \frac{1}{4} \ln \left | 4x-1 \right | +C$$	Back-substitution

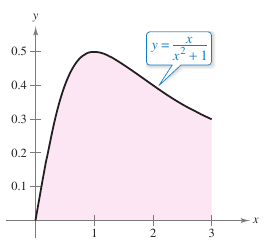
Example 5.2.3 Finding Area with the Log Rule, Part 2

Figure 5.2.1

Find the area for the region bounded by the graph for $$y=\frac{x}{x^2+1}$$ the \(x\)-axis and the line \(x=3\). Solution Look for quotients where the numerator is the derivative for the denominator. The area for the definite integral $$\int_{0}^{3} \frac{x}{x^2+1}\:dx,$$ is shown in Figure 5.2.1. Let \(u=x^2+1\), then \({u}'=2x\). To apply the Log Rule, multiply and divide by two, as shown below. $$\int_{0}^{3} \frac{x}{x^2+1}\:dx$$ $$=\frac{1}{2} \int_{0}^{3} \frac{2x}{x^2+1}\:dx$$     Multiply and divide by two. $$=\frac{1}{2} \left [ \vphantom{ \frac{3}{4} } \ln(x^2+1) \right ]_{0}^{3}$$     Apply Theorem 5.2.1 Part 2. $$=\frac{1}{2} ( \ln 10 - \ln 1)$$ $$=\frac{1}{2} \ln 10 $$     \(\ln 1 = 0\) \(\approx 1.151\)

Example 5.2.4 Recognizing Quotient Forms for the Log Rule

Evaluating antiderivatives involving logarithms can produce forms that look quite different but are still equivalent. For example, both

\(\ln \left | (3x+2)^{1/3}) \right |+C\)

and

\(\ln \left | 3x+2 \right |^{1/3}+C\)

are equivalent to the antiderivative listed in Example 5.2.4(d).

Integrals to which the Log Rule can be applied often appear in disguised form. For example, when a rational function has a numerator with degree greater than or equal to the denominator, division may reveal a form where the Log Rule applies. This is shown in Example 5.2.5.

Example 5.2.5 Using Long Division Before Integrating

Find the indefinite integral.

$$ \int \frac{x^2+x+1}{x^2+1}\:dx$$

Solution Begin by using long division to rewrite the integrand.

Substitute into the original integral yields.

$$ \int \frac{x^2+x+1}{x^2+1}\:dx$$	$$=\int \left ( 1+\frac{x}{x^2+1} \right )\:dx$$	Rewrite using long division.
	$$=\int \: dx+ \frac{1}{2} \int \frac{2x}{x^2+1}\:dx$$	Rewrite as two integrals.
	$$=x+ \frac{1}{2} \ln(x^2+1)+C.$$	Integrate

2 Check this result by differentiating to obtain the original integrand.

Example 5.2.6 Change Variables with the Log Rule

Find the indefinite integral.

$$\int \frac{2x}{(x+1)^2}\:dx$$

Solution Let \(u=x+1\), then \(du=dx\) and \(x=u-1\).

$$\int \frac{2x}{(x+1)^2}\:dx$$	$$=2 \int \frac{2(\color{red}{u-1})}{\color{red}{u^2}}\: du$$	Substitute
	$$=2 \int \left ( \frac{u}{u^2}- \frac{1}{u^2} \right ) \: du$$	Rewrite as two fractions.
	$$= 2 \int \frac{du}{u} - 2 \int \: u^{-2}\:du$$	Rewrite as two integrals.
	$$=2 \ln \left | u \right | -2 \left ( \frac{u^{-1}}{-1} \right )+C$$	Integrate.
	$$=2 \ln \left | u \right |+ \frac{2}{u} + C$$	Simplify
	$$=2 \ln \left | x+1 \right |+ \frac{2}{x+1} + C$$	Back substitute

Check this result by differentiating to obtain the original integrand.

Examples 5.2.5 and 5.2.6 involve rewriting a disguised integrand so that it fits one or more basic integration formulas. To master recognizing a disguised integrand think about integration's “form-fitting” nature. In this sense, integration is not nearly as straightforward as differentiation.

Differentiation takes the form

“Here is the question; what is the answer?”

Integration is more like

“Here is the answer; what is the question?”

Guidelines for Integration

1. Learn the integration formulas. The discussion has covered 12 formulas so far. This will expand to 20 later in the discussion.
2. Find an integration formula that resembles the integrand, all or in part, and, by trial and error, find a \(u\) that will make the integrand conform to the formula.
3. When \(u\)-substitution fails, try altering the integrand. Use a trigonometric identity, multiplication and division by the same quantity, addition and subtraction with the same quantity, or long division. Be creative. Be imaginative.
4. Use software to find antiderivatives symbolically.

Example 5.2.7 \(u\)--Substitution and the Log Rule

Solve the differential equation

$$\frac{dy}{dx} = \frac{1}{x \ln x}.$$

Solution The solution can be written as an indefinite integral.

$$y=\int \frac{1}{x \ln x}\: dx$$

Because the integrand is a quotient whose denominator is raised to the first power, try applying the Log Rule. There are three basic choices for \(u\). The choices

\(u=x\:\:\:\:\text{and}\:\:\:\:u=x \ln x\)

fail to fit the \({u}'/u\) form for the Log Rule. Choice three, \(u=\ln x\) produces \({u}'=1/x\). This yields the following.

$$\int \frac{1}{x \ln x}\: dx$$	$$=\int \frac{1/x}{\ln x}\:dx$$	Divide numerator and denominator by \(x\).
	$$=\int \frac{{u}'}{u}\: dx$$	Substitute \(u=\ln x\)
	\(=\ln \left | u \right | +C\)	Apply Log Rule
	\(=\ln \left | \ln x \right | +C\)	Back substitution

The solution is \(y=\ln \left | \ln x \right | +C\). Verify the answer by differentiating the answer.

Integrals with Trigonometric Function

Examples 5.2.8 and 5.2.9 describe integrating \(\tan\) and \(\sec\) using the Log Rule.

Example 5.2.8 Using a Trigonometric Identity

Find

$$\int \tan x \:dx.$$

Solution This does not fit the formulas described in Section 4.1. However, applying a trigonometric identity yields

$$\int \tan x \:dx= \int \frac{\sin x}{\cos x}\:dx.$$

Knowing that \(D_x[\cos x]= - \sin x\), let \(u= \cos x\) and write

$$\int \tan x \:dx$$	$$= -\int \frac{-\sin x}{\cos x}\:dx$$	Apply trigonometric identity and multiply and divide by -1
	$$=- \int \frac{{u}'}{u}\:dx$$	Substitute \(u=\cos x\)
	\(=- \ln \left | u \right | + C\)	Apply Log Rule
	\(= - \ln \left | \cos x \right | + C.\)	Back substitute

Example 5.2.8 uses a trigonometric identity to derive an integration rule for the tangent function. Example 5.2.9 multiplies and divides by the same quantity to derive an integration rule for the secant function.

Example 5.2.9 Derivation for the Secant Formula

Find

$$\int \sec x \:dx.$$

Solution Consider the following procedure.

$$\int \sec x \:dx$$	$$=\int \sec x \left ( \frac{\sec x + \tan x}{\sec x + \tan x} \right )\:dx$$
	$$= \int \frac{\sec^2 x+ \sec x \tan x}{\sec x + \tan x}\:dx$$

Letting \(u\) be the denominator for this quotient produces

\(u= \sec x + \tan x\)

and

\({u}'= \sec x \tan x + \sec^2 x.\)

Substitute these into the original equation produces.

$$\int \sec x \:dx$$	$$= \int \frac{\sec^2 x+ \sec x \tan x}{\sec x + \tan x}\:dx$$	Rewrite the integrand
	$$=- \int \frac{{u}'}{u}\:dx$$	Substitute \(u= \sec x + \tan x\)
	\(=- \ln \left | u \right | + C\)	Apply Log Rule
	\(= - \ln \left | \sec x + \tan x \right | + C.\)	Back substitute

Integrals for the Six Basic Trigonometric Functions

$$\int \sin u \:du= - \cos u + C$$	$$\int \cos u \:du= \sin u +C$$
$$\int \tan u \:du= - \ln \left | \cos u \right | +C$$	$$\int \cot u\: du= \ln \left | \sin u \right | +C$$
$$\int \sec u \:du= \ln \left | \sec u + \tan u \right | +C\:\:\:\:$$	$$\int \csc u \:du= - \ln \left | \csc u + \cot u \right | +C$$

Example 5.2.10 Integrating Trigonometric Functions

Evaluate

$$\int_{0}^{\pi/4} \sqrt{1+ \tan^2 x}\:dx.$$

Solution Using \(1+\tan^2 x = \sec^2 x\), write

$$\int_{0}^{\pi/4} \sqrt{1+ \tan^2 x}\:dx$$	$$=\int_{0}^{\pi/4} \sqrt{\sec^2 x}\:dx.$$
	$$=\int_{0}^{\pi/4} \sec x\:dx$$	\(\sec x \geq 0 \:\text{for}\: 0 \leq x \leq \frac{\pi}{4}\)
	$$=\ln \left. \left | \sec x + \tan x \right | \vphantom{ \frac{3}{4} } \right ]_{0}^{\pi/4}$$
	\(= \ln ( \sqrt{2}+1) - \ln 1\)
	\(\approx 0.881.\)

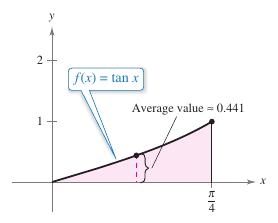
Example 5.2.11 Finding an Average Value

Figure 5.2.2

Find the average value for \(f(x)=\tan x\) on the interval \([0,\pi/4]\). Solution The average value is about 0.441, as shown in Figure 5.2.2.

Internal Links

Parent Article: Calculus I 05 Logarithmic, Exponential, and Other Transcendental Functions