Calculus I 05.05 Bases Other than e and Applications
| Previous | Calculus I 05.04 Exponential Functions: Differentiation and Integration |
| Next | Calculus I 05.06 Inverse Trigonometric Functions: Differentiation |
Contents
5.5 Bases Other than \(e\) and Applications
- Define exponential functions that have bases other than \(e\).
- Differentiate and integrate exponential functions that have bases other than \(e\).
- Use exponential functions to model compound interest and exponential growth.
Bases Other than \(e\)
The base for a natural exponential function is \(e\). This "natural" base assigns meaning to a general base \(a\).
Definition 5.5.1 Exponential Function to a Base \(a\)
If \(a\) is a positive real number, \(a \ne 1\), and \(x\) is any real number, then the exponential function to the base \(a\) is denoted by \(a^x\) and is defined by
- \(a^x=e^{(\ln a)x}.\)
If \(a=1\), then \(y=1^x\) is a constant function.
These functions obey the usual laws for exponents. For example, here are some familiar properties.
|
2. \(a^xa^y=a^{x+y}\) |
3. |
$$\frac{a^x}{a^y}=a^{x-y}$$ |
|
4. \((a^x)^y=a^{xy}\) |
When modeling the half-life for a radioactive sample, the base \(\frac{1}{2}\) is used in the exponential model. Half-life is the years required for half of the atoms in a sample to radioactively decay.
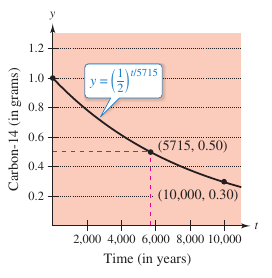
Example 5.5.1 Radioactive Half-Life Model
|
|
Carbon-14's half-file is about 5,715 years. A carbon-14 sample weighs one gram. How much will remain in 10,000 years?
Notice that when \(t=5715\), the amount is reduced to half the original amount.
When \(t=11,430\), the amount is reduced to a quarter the original amount, and so on. To find the amount remaining after 10,000 years, let \(t=10,000\), and
as shown in Figure 5.5.1. |
Logarithmic functions to bases other than \(e\) are defined in much the same way as exponential functions to other bases are defined.
Definition 5.5.1 Logarithmic Function to Base \(a\)
If \(a\) is a positive real number, \(a \ne 1\), and \(x\) is any positive real number, then the logarithmic function to the base \(a\) is denoted by \( \log_a x\) and is defined as
- $$\log_a x = \frac{1}{\ln a} \ln x.$$
Logarithmic functions to base \(a\) have properties similar to the natural logarithmic function given in Theorem 5.1.2. This assumes \(x\) and \(y\) are positive numbers and \(n\) is rational.
|
Log for 1 | |
|
Log for a product | |
|
Log for a power | |
|
$$log_a \frac{x}{y}= \log_a x - \log_a y$$ |
Log for a quotient |
From Definition 5.5.1, it follows that \(f(x)=a^x\) and \(g(x)=\log_a x\) are inverse functions for each other.
Properties for Inverse Functions
- 1. \(y=a^x\) if and only if \(x=\log_a y\)
- 2. \( a^{\log_a x}=x\), for \(x>0\)
- 3. \( \log_a a^x=x\), for all \(x\)
The logarithmic function to the base 10 is called the common logarithmic function. For common logarithms,
- \(y=10^x\) if and only if \(x=\log_10 y.\) Inverse Function Property
Example 5.5.2 Evaluating Bases Other than \(e\)
Solve for \(x\) in each equation.
|
$$3^x=\frac{1}{81}$$ |
b. \(\log_2 x = -4\) |
Solution
|
a. Apply the logarithmic function
|
b. Apply the logarithmic function
|
Differentiation and Integration
There are three methods to differentiate exponential and logarithmic functions to other bases, use \(a^x\) and \(log_a x\) and the natural exponential and logarithmic functions, (2) use logarithmic differentiation, and, use the differentiation rules for bases other than \(e\) given in Theorem 5.5.1.
Theorem 5.5.1 Derivatives for Bases Other than \(e\)
Let \(a\) be a positive real number, \(a \ne 1\), and let \(u\) be a differentiable function for \(x\).
|
$$\textbf{2.}\:\: \frac{d}{dx} \left [ a^u \right ] = ( \ln a ) a^u \frac{du}{dx}$$ |
|
$$\textbf{4.}\:\: \frac{d}{dx} \left [ \log_a u \right ] = \frac{1}{(\ln a)x} \frac{du}{dx}$$ |
Proof By definition,
- \(a^x=e^{(\ln a)x}.\)
Prove Property 1 by letting
- \(u=(\ln a)x\)
and differentiating with base \(e\) to obtain
- $$\frac{d}{dx} \left [ a^x \right ]=\frac{d}{dx} \left [ e^{(\ln a)x} \right ]=e^u \frac{du}{dx}=e^{(\ln a)x}(\ln a) =(\ln a)a^x.$$
Prove Property 3 in a similar manner
- $$\frac{d}{dx} \left [ \log_a x \right ]=\frac{d}{dx}\left [ \frac{1}{\ln a} \ln \right ]=\frac{1}{\ln a} \left ( \frac{1}{x} \right ) =\frac{1}{(\ln a)x}.$$
The Second and Fourth Properties are proved using the Chain Rule.
Example 5.5.3 Differentiating Functions to Other Bases
Find the derivative for each function.
| a. | \(y=2^x\) | b. | \(y=2^{3x}\) | c. | \(y=\log_10 \cos x\) | d. |
$$y=\log_3 \frac{\sqrt{x}}{x+5}$$ |
Solution
- $$\textbf{a.}\:\: {y}'=\frac{d}{dx} \left [ 2^x \right ]=( \ln 2)2^x$$
- $$\textbf{b.}\:\: {y}'=\frac{d}{dx} \left [ 2^{3x} \right ]=( \ln 2)2^{3x}(3)=(3 \ln 2) 2^{3x}$$
- $$\textbf{c.}\:\: {y}'=\frac{d}{dx} \left [ \log_10 \cos x \right ]=\frac{- \sin x}{(\ln 10) \cos x}=-\frac{1}{\ln 10} \tan x$$
- d. Before differentiating, rewrite the function using logarithmic properties.
- $$y=\log_3 \frac{\sqrt{x}}{x+5}=\frac{1}{2} \log_3 x- \log_3(x+5)$$
Next, apply Theorem 5.5.1 to differentiate the function.
|
$$=\frac{d}{dx} \left [ \frac{1}{2} \log_3 x- \log_3(x+5) \right ]$$ |
|
$$=\frac{1}{2(\ln 3)x}- \frac{1}{(\ln 3)(x+5)}$$ | |
|
$$=\frac{5-x}{2(\ln 3)x(x+5)}$$ |
Occasionally, an integrand involves an exponential function to a base other than \(e\). When this occurs, there are two options, convert to base \(e\) using the formula \(a^x=e^{(\ln a)x}\) and then integrate, or integrate directly, using the integration formula
- $$\int a^x\:dx=\left ( \frac{1}{\ln a} \right ) a^x +C$$
which follows from Theorem 5.5.1.
Example 5.5.4 Integrating an Exponential Function to Another Base
Find
- $$\int 2^x\:dx.$$
Solution
- $$\int 2^x\:dx= \frac{1}{\ln 2} 2^x +C$$
The Power Rule, \(D_x[x^n]=n x^{n-1}\), requires a rational number for the exponent. Theorem 5.5.2 extends it to cover any real \(n\) value.
Theroem 5.5.2 The Power Rule for Real Exponents
Let \(n\) be any number, and let \(u\) be a differentiable function for \(x\).
- $$\textbf{1.}\:\frac{d}{dx} \left [ x^n \right ] = n x^{n-1}\:\:\:\:\textbf{2.}\:\frac{d}{dx} \left [ u^n \right ]=n u^{n-1}\:\frac{du}{dx}$$
Example 5.5.5 compares the derivatives for four function types. Each function uses a different differentiation formula, depending on whether the base and the exponent are constants or variables.
Example 5.5.5 Comparing Variables and Constants
Find the derivative for each function.
In Example 5.5.5(d) there is no simple differentiation rule for calculating the derivative for \(y=x^x\). In general, when \(y=u(x)^{v(x)}\), logarithmic differentiation is needed.
Exponential Function Applications
|
The amount \(P\) dollars is deposited in an account at an annual interest rate \(r\), in decimal form. What is the balance in the account after one year? The answer depends on how many \(n\) times the interest is compounded according to the formula
For example, the result for a $1,000 deposit at 8% interest compounded \(n\) times a year is shown in Table 5.5.1. As \(n\) increases, the balance \(A\) approaches a limit. To evaluate this limit apply Theorem 5.5.3. Test the theorem's reasonableness by evaluating
for several \(x\)-values, as shown in Table 5.5.2. Theorem 5.5.3 A Limit Involving \(e\)
Consider Theorem 5.5.3 and take another look at the formula for the balance \(A\) in an account in which the interest is compounded \(n\) times per year. Taking the limit as \(n\) approaches infinity produces
This limit produces the balance after continuous compounding for one year. For a $1,000 deposit at 8.00% interest compounded continuously, the balance after one year is \(A = 1000e^{0.08} \approx $1,083.29\). | ||||||||||||||||||||||||||||||||||||||||||
Compound Interest Formulas
Let \(P\) = deposit amount, \(t\) = years, \(A\) = balance after \(t\) years, \(r\) = anual interest rate, and \(n\) = compoundings per year.
| 1. Compounded \(n\) times per year: |
$$A= P \left ( 1 + \frac{r}{n} \right )^{nt}$$ |
| 2. Compounded continuously: \(A=Pe^{rt}\) |
Example 5.5.6 Continuous, Quarterly, and Monthly Compounding
A bank account has $2500 and pays a 5% annual interest rate. Find the balance in the account at the end of 5 years when the interest is compounded (a) quarterly, (b) monthly, and (c) continuously.
Solution
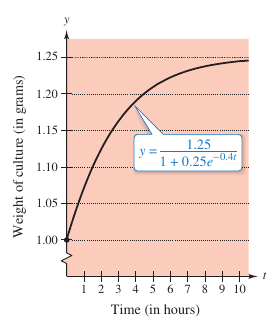
Example 5.5.7 Bacterial Culture Growth
|
|
A bacterial culture is growing according to the logistic growth function
where \(y\) is the culture's weight in grams and \(t\) is the time in hours. Find the weight after (a) 0 hours, (b) 1 hour, (c) 10 hours, and (d) what is the limit as \(t\) approaches infinity?
d. Take the limit as \(t\) approaches infinity produces
The graph for the culture weight is shown in Figure 5.5.2. |
Internal Links
Parent Article: Calculus I 05 Logarithmic, Exponential, and Other Transcendental Functions