Calculus II 08.03 Trigonometric Integrals

Previous	Calculus II 08.02 Integration by Parts
Next	Calculus II 08.04 Trigonometric Substitution

8.3 Trigonometric Integrals

• Use sine and cosine powers to solve trigonometric integrals.
• Use secant and tangent powers to solve trigonometric integrals.
• Solve trigonometric integrals involving sine-cosine products with different angles.

Integrals with Sine and Cosine Powers

Integrals with sine and cosine powers have the form

$$ \int \sin^{m} x \: \cos^{n} x \:dx \text{ and } \int \sec^{m} x \: \tan^{n} x \:dx $$

where either \(m\) or \(n\) is a positive integer. To find their antiderivatives break them up into trigonometric combinations for which the Power Rule applies.

For example, evaluate

$$ \int \sin^{5} x \: \cos x \:dx $$

with the Power Rule by letting \(u=\sin x\). Then, \(du=\cos x\:dx\) which produces

$$ \int \sin^{5} x \: \cos x \:dx = \int u^{5}\:du = \frac{u^{6}}{6}+C= \frac{\sin^{6} x}{6}+C $$

Use the following identities to break up \(\int \sin^{m} x \: \cos^{n} x \:dx \) into forms where the Power Rule applies.

\( \sin^{2} x + \cos^{2} x = 1 \)	Pythagorean identity
$$ \sin^{2} x = \frac{ 1 - \cos 2x}{2} \:\:\:\: $$	Half-angle identity for \( \cos^{2} x \)
$$ \cos^{2} x = \frac{ 1 + \cos 2x}{2} $$	Half-angle identity for \( \cos^{2} x \)

Guidelines for Evaluating Integrals with Sine and Cosine Powers

1. When the sine power is odd and positive, save one sine factor and convert the remaining factors to cosines. Then expand and integrate.

$$ \int \sin^{ \color{red}{\overbrace{\color{black}{2k+1}}^{Odd}}} x \cos^{n} x\:dx = \int \color{Red}{ \overbrace{ \color{black}{(\sin^{2} x)^{k}}}^{\text{Convert to cosines}}} \cos^{n} x \color{red}{ \overbrace{\color{black}{\sin x\:dx}}^{\text{Save for }du}} = \int (1- \cos^{2} x)^{k} \cos^{n} x \sin x\:dx$$

2. When the cosine power is odd and positive, save one cosine factor and convert the remaining factors to sines. Then expand and integrate.

$$ \int \sin^{m} x \cos^{ \color{red}{\overbrace{\color{black}{2k+1}}^{Odd}}} x\:dx = \int \sin^{m} x \color{Red}{ \overbrace{ \color{black}{(\cos^{2} x)^{k}}}^{\text{Convert to sines}}} \:\: \color{red}{ \overbrace{\color{black}{\cos x\:dx}}^{\text{Save for }du}} = \frac{1}{2} \int \sin^{m} x \: (1- \sin^{2} x)^{k} \cos x \:dx$$

3. When both sine and cosine powers are even and positive, repeatedly apply the identities.

$$ \sin^{2} x = \frac{1-\cos 2x}{2} \text{ and } \cos^{2} x = \frac{1 + \cos 2x}{2} $$

to convert the cosine powers from even to odd. Then proceed as in 2.

Example 8.3.1 Sine Power is Odd and Positive

Find

$$ \int \sin^{3} x \cos^{4} x\:dx.$$

Solution The power for \( \sin \) is odd and positive. The power for \( \cos \) is even and positive. Use guideline 1 from above. The Power Rule can use \(u=\cos x\) so save one sine factor to form \(du\) and convert the remaining sine factors to cosines.

$$ \int \sin^{3} x \cos^{4} x\:dx $$	$$= \int \sin^{2} x \cos^{4} x \: (\sin x) x\:dx $$	Rewrite
	$$= \int (1 - \cos^{2} x)\: \cos^{4} x\: \sin x\:dx $$	Trigonometric identity
	$$= \int ( \cos^{4} x - \cos^{6} x)\: \sin x\:dx $$	Multiply
	$$= \int \cos^{4} x - \: \sin x\:dx - \int \cos^{6} x\: \sin x\:dx $$	Rewrite
	$$= - \int \cos^{4} x \:(- \sin x)\:dx + \int \cos^{6} x\:(- \sin x)\:dx $$
	$$= \frac{ \cos^{5} x}{5}+ \frac{\cos^{7} x}{7} + C $$	Integrate

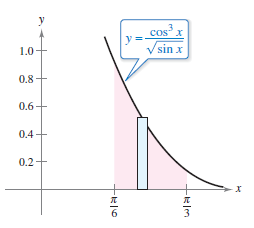
Example 8.3.2 Cosine Power is Odd and Positive

The region's area is \(\approx\) 0.239. Figure 8.3.1

Evaluate $$ \int_{\pi/6}^{\pi/3} \frac{\cos^{3} x}{\sqrt{\sin x}}\:dx$$ Solution The \( \cos \) power is odd and positive. The \( \sin \) power is negative but neither even or odd because it is a fraction, not an integer. Use guideline 2 from above. The Power Rule can use \(u=\sin x\) so save one sine factor to form \(du\) and convert the remaining cosine factors to sines. $$ \int_{\pi/6}^{\pi/3} \frac{\cos^{3} x}{\sqrt{\sin x}}\:dx $$ $$= \int_{\pi/6}^{\pi/3} \frac{\cos^{2} x \cos x}{\sqrt{\sin x}}\:dx $$ $$= \int_{\pi/6}^{\pi/3} \frac{ (1-\sin^{2} x)(\cos x)}{\sqrt{\sin x}}\:dx $$ $$= \int_{\pi/6}^{\pi/3} [(\sin x)^{-1/2}-(\sin x)^{3/2}]\cos x\:dx $$ $$= \left[ \frac{(\sin x)^{-1/2}}{1/2}- \frac{(\sin x)^{5/2}}{5/2} \right]_{\pi/6}^{\pi/3} $$ $$= 2 \left( \frac{(\sqrt{3}}{2}\right)^{1/2}- \frac{2}{5} \left( \frac{\sqrt{3}}{2} \right)^{5/2} - \sqrt{2} + \frac{\sqrt{32}}{80}\approx 0.239 $$ Figure 8.3.2 shows the region's area as \( \approx 0.239\).

Example 8.3.3 Cosine Power is Even and Nonnegative

Find

$$ \int \cos^{4} x \:dx $$

Solution The cosine power is even and nonnegative. The sine power is even and nonnegative, \(m=0\). Use guideline 3 from above. The \(\cos\) can be replaced by

$$ \left( \frac{1+\cos 2x}{2} \right)^{2} $$ using the half-angle identity. Then integration can proceed

$$ \int \cos^{4} x \:dx $$	$$= \int \left( \frac{1+\cos 2x}{2} \right)^{2} \:dx $$	Half-angle identity
	$$= \int \left( \frac{1}{4} + \frac{\cos 2x}{2} + \frac{\cos^{2} 2x}{4} \right) \:dx $$	Expand
	$$= \int \left[ \frac{1}{4} + \frac{\cos 2x}{2} + \frac{1}{4} \left( \frac{1+\cos 4x}{2} \right) \right] \:dx $$	Half-angle identity, again
	$$= \frac{3}{8} \int \:dx + \frac{1}{4} \int 2 \cos 2x \:dx + \frac{1}{32} \int 4 \cos 4x \:dx $$	Rewrite
	$$= \frac{3x}{8} + \frac{\sin 2x}{4} + \frac{\sin 4x}{32} + C $$	Integrate

Wallis's[1] Formulas

• Wallis's Product[2]
• Wallis' Integrals[3]

In Example 8.3.3, when the definite integral is evaluated from 0 to \(\pi / 2\)

$$ \int_{0}^{\pi/2} \cos^{4} x \:dx $$	$$= \left[ \frac{3x}{8} + \frac{\sin 2x}{4} + \frac{\sin 4x}{32} \right]_{0}^{\pi/2} $$
	$$= \left( \frac{3 \pi}{16}+0 +0 \right) - (0+0+0)= \frac{3 \pi}{16} $$

Note that only \(\frac{3 \pi}{16} \) contributes to the solution. This observation is described by John Wallis (1616-1703) in the formulas below.
1. If \(n\) is odd \( (n \geqslant 3) \), then

$$ \int_{0}^{\pi /2 \cos^{n} x\:dx} = \left(\frac{2}{3}\right)\left(\frac{4}{5}\right)\left(\frac{6}{7}\right) \cdots \left(\frac{n-1}{n}\right) $$

2. If \(n\) is even \( (n \geqslant 2) \), then

$$ \int_{0}^{\pi /2 \cos^{n} x\:dx} = \left(\frac{1}{2}\right)\left(\frac{3}{4}\right)\left(\frac{5}{6}\right) \cdots \left(\frac{n-1}{n}\right)\left(\frac{\pi}{2}\right)$$

These formulas are also valid when \(\cos^{n} x\) is replaced by \( \sin^{2} x\).

Integrals with Secant and Tangent Powers

Integrals with the form \( \int \sec^{m} x \:\tan^{n} x \: dx \) can be integrated using the following guidelines. 1. When the secant power is even and positive, save a secant-squared factor and convert the remaining factors to tangents. Then expand and integrate.

$$ \int \sec^{ \color{red}{\overbrace{\color{black}{2k}}^{Even}}} x \tan^{n} x\:dx = \int \color{Red}{ \overbrace{ \color{black}{(\sec^{2} x)^{k-1}}}^{\text{Convert to tangents}}} \tan^{n} x \: \color{red}{ \overbrace{\color{black}{\sec^{2} x\:dx}}^{\text{Save for }du}} = \int (1- \tan^{2} x)^{k-1} \tan^{n} x \sec^{2} x\:dx$$

2. When the tangent power is odd and positive, save one secant-tangent factor and convert the remaining factors to secants. Then expand and integrate.

$$ \int \sec^{m} x \tan^{ \color{red}{\overbrace{\color{black}{2k+1}}^{Odd}}} x\:dx = \int \sec^{m-1} x \color{Red}{ \overbrace{ \color{black}{(\tan^{2} x)^{k}}}^{\text{Convert to secants}}} \:\: \color{red}{ \overbrace{\color{black}{\sec x \tan x\:dx}}^{\text{Save for }du}} = \int \sec^{m-1} x \: ( \sec^{2} x - 1)^{k} \sec x \tan x\:dx$$

3. When there is no secant factor and the tangent power is even and positive, convert a tangent-squared factor to a secant-squared factor, then expand and repeat if necessary.

$$ \int \tan^{n} x\:dx = \int tan^{n-2} x \:\color{red}{ \overbrace{\color{black}{ (\tan^{2} x)}}^{\text{Convert to secants}}} \:dx= \int \tan^{n-2} x \:(\sec^{2} x-1)\:dx $$

4. When the secant power \(m\) is odd and positive

$$\int \sec^{m} x \: dx $$

use integration by parts as in Example 8.2.5.

Example 8.3.4 Tangent Power is Odd and Positive

Find

$$\int \frac{\tan^{3} x}{\sqrt{\sec x}} \:dx $$

Solution The tangent power is odd and positive, use guideline 1 from above. The Power Rule works best with \(u=\sec x\), save the factor \((\sec x \: \tan x )\) to form \(du\) and convert the remaining tangent factors to secants.

$$ \int \frac{\tan^{3} x}{\sqrt{\sec x}} \:dx $$	$$= \int (\sec x)^{-1/2} \tan^{3} x\: dx $$
	$$= \int \left(\sec x \right)^{-3/2} \tan^{2} x \: (\sec x \tan x)\: dx$$
	$$= \int (\sec x)^{-3/2} (\sec^{2} x -1) \: (\sec x \tan x)\: dx $$
	$$= \int \left[(\sec x)^{1/2} - (\sec x)^{-3/2} \right] \: (\sec x \tan x)\: dx $$
	$$= \frac{2}{3} (\sec x)^{3/2} + 2(\sec x)^{-1/2} + C $$

Example 8.3.5 Secant Power is Even and Positive

Find

$$ \int \sec^{4} 3x \tan^{3} 3x \:dx $$

Solution The tangent power is odd and positive, use guideline 2 from above. Let \(u=\tan 3x\), then \(du=3 \sec^{2} 3x\:dx\) which produces

$$ \int \sec^{4} 3x \tan^{3} 3x \:dx $$	$$= \int \sec^{3} 3x \tan^{3} 3x\: (\sec^{2} 3x)\:dx $$
	$$= \int ( 1 + \tan^{2} 3x) \tan^{3} 3x\: (\sec^{2} 3x)\:dx $$
	$$= \frac{1}{3} \left( \frac{ \tan^{4} 3x}{4} + \frac{ \tan^{6} 3x}{6} \right) + C $$
	$$= \frac{ \tan^{4} 3x}{12} + \frac{ \tan^{6} 3x}{18} + C $$

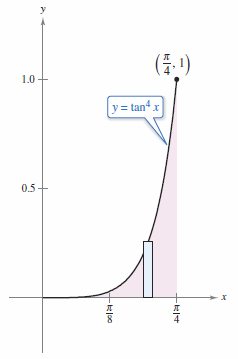
Example 8.3.6 Tangent Power is Even

The region's area is \(\approx\) 0.119. Figure 8.3.2

Evaluate $$ \int_{0}^{\pi/4} \tan^{4} x \:dx $$ Solution The tangent power is even and positive, use guideline 3 from above. Because there are no secant factors convert a tangent-squared factor into a secant squared-factor. $$ \int \tan^{4} x \:dx $$ $$= \int \tan^{4} x \:dx $$ $$= \int \tan^{2} x \: ( \sec^{2} x -1) \:dx $$ $$= \int \tan^{2} x \: \sec^{2} x ) \:dx - \displaystyle{ \int } \tan^{2} x \: dx\) \(= \displaystyle{ \int } \tan^{2} x \: \sec^{2} x ) \:dx - \displaystyle{ \int } ( \sec^{2} x -1)\: dx \) \(= \frac{ \tan^{3} x}{3} - \tan x + x + C \) Use \([0, \pi /4]\) to evaluate the definite integral. \( \displaystyle{ \int_{0}^{\pi/4} } \tan^{4} x \:dx \) \(= \Bigg[ \frac{\tan^{3}}{3} - \tan x + x \Bigg]_{0}^{\pi/4} \) \(= \frac{1}{3} - 1 + \frac{\pi}{4} \) \( \approx 0.119\) The region represented by the definite integral is shown in Figure 8.3.2. Using Simpson's Rule[4] with \(n=18\) will approximate the actual integral to within 0.00001.

Example 8.3.7 Converting to Sines and Cosines

Find

\( \displaystyle{ \int } \frac{\sec x}{\tan^{2} x} \:dx \)

Solution The guidelines above to not apply. Simplify the integrand by converting secants to cosines.

\( \displaystyle{ \int } \frac{\sec x}{\tan^{2} x} \:dx \)	\( \displaystyle{ \int } \Bigg( \frac{ 1}{\cos x} \Bigg) \Bigg( \frac{\cos x}{\sin x} \Bigg)^{2} \:dx \)	Convert secant to cosine and tangent to cosine / sine.
	\(= \displaystyle{ \int } (\sin x)^{-2}(\cos x) \: dx \)
	\(= (\sin x)^{-1} + C \)
	\(= (\csc x) + C \)

Integrals Involving Sine-Cosine Products with Different Angles

Integrals involving sine and cosine products with two different angles occur in many applications. The following product-to-sum identities can simplify the integrand. $$ \sin mx \sin nx = \frac{1}{2} (\cos [(m-n)x]-\cos[(m+n)x]) $$ $$ \sin mx \cos nx = \frac{1}{2} (\sin [(m-n)x]+\sin[(m+n)x]) $$ $$ \cos mx \cos nx = \frac{1}{2} (\cos [(m-n)x]+\cos[(m+n)x]) $$

Example 8.3.8 Using Product-to-Sum Identities on an Integral with two angles

Find

\( \displaystyle{ \int } \sin 5x \cos 4x \: dx\)

Solution Using the second product-to-sum identity from above produces

\( \displaystyle{ \int } \sin 5x \cos 4x \: dx\)	\(= \frac{1}{2} (\sin x + sin 9x)\: dx \)
	\(= \frac{1}{2} \Bigg( - \cos x - \frac{\cos 9x}{9} + C \)
	\(= - \frac{\cos x}{2}- \frac{\cos 9x}{18} + C \).

The same strategy used for integrals with tangent and secant powers applies to integrals with cotangent and cosecant powers. For complex evaluations convert the entire integrand to sine and cosine powers.

Internal Links

Parent Article: Calculus II 08 Integration Techniques