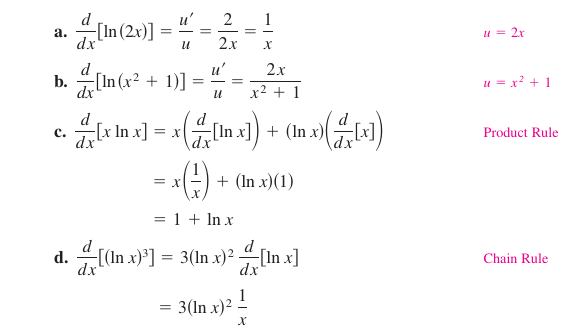Difference between revisions of "Calculus I 05.01 The Natural Logarithmic Function: Differentiation"
(→Example 5.1.1) |
(No difference)
|
Latest revision as of 00:25, 5 December 2020
| Previous | Calculus I 04 Integration |
| Next | Calculus I 05.02 The Natural Logarithmic Function: Integration |
Contents
- 1 5.1 The Natural Logarithmic Function: Differentiation
- 1.1 The Natural Logarithmic Function[1]
- 1.2 The Number \(e\)[2]
- 1.3 Natural Logarithmic Function Derivatives
- 1.3.1 Theorem 5.1.3 Natural Logarithmic Function Derivative
- 1.3.2 Example 5.1.3 Differentiating Logarithmic Functions
- 1.3.3 Example 5.1.4 Differentiation with Logarithmic Properties, Square Root
- 1.3.4 Example 5.1.5 Differentiation with Logarithmic Properties, Quotient
- 1.3.5 Example 5.1.6 Logarithmic Differentiation
- 1.3.6 Theorem 5.1.4 Derivatives Involving Absolute Value
- 1.3.7 Example 5.1.7 Derivative Involving Absolute Value
- 1.3.8 Example 5.1.8 Finding Relative Extrema
- 2 Internal Links
5.1 The Natural Logarithmic Function: Differentiation
- Natural logarithmic function properties.
- The definition for the number \(e\).
- Evaluate functions with natural logarithms.
The Natural Logarithmic Function[1]
Recall the General Power Rule
|
General Power Rule |
has an important disclaimer—it doesn’t apply when \(n=-1\). Consequently, thus far in the discussion, there is no way to find an antiderivative for functions like \(f(x)=1/x\). Using natural logarithms and the Second Fundamental Theorem of Calculus can find an antiderivative for such a function. This particular function is the natural logarithmic function.
Definition 5.1.1 Natural Logarithmic Function
The natural logarithmic function is defined by
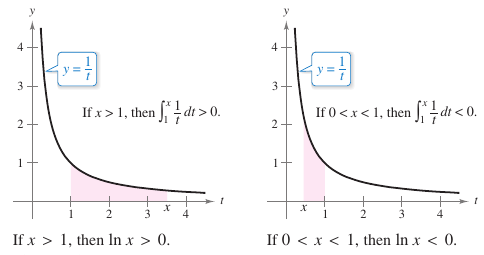
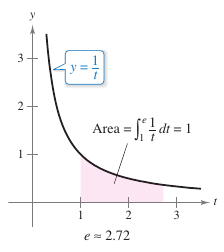
- $$\ln x = \int_{1}^{x} \frac{1}{t}\:dt,\:\:\:x>0.$$
The domain for the natural logarithmic function is all real positive numbers.
From Definition 5.1.1, \(\ln x\) is positive for \(x>1\) and negative for \(0<x<1\), as shown in Figure 5.1.1. Because the upper and lower integration limits are equal when \(x=1\), \(\ln(1)=0\).
|
|
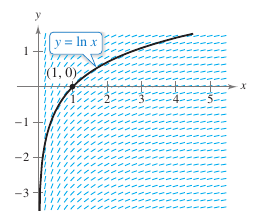
To sketch the graph for \(y=\ln x\), think about the natural logarithmic function as an antiderivative given by the differential equation
Figure 5.1.2 is a graph called a slope field, or direction field, showing small line segments following the slope for \(1/x\). The graph for \(y= \ln x\) is the solution that passes through the point \((1,0)\). Theorem 5.1.1 Natural Logarithmic Function PropertiesThe natural logarithmic function has the following properties. |
|
|
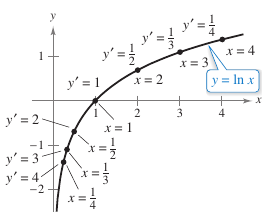
Proof The domain for \(f(x)=\ln x\) is \((0,\infty)\) by Definition 5.1.1. The function is continuous because it is differentiable. It is increasing because its derivative
is positive for \(x>0\), as shown in Figure 5.1.3. It is concave downward because
is negative for \(x>0\). The proof that \(f\) is one-to-one is left as an exercise. The following limits imply that its range is the entire real number line
and
|
The properties in Theorem 5.1.2 are characteristic for all logarithms and are easily proved using Definition 5.1.1.
Theorem 5.1.2 Logarithmic Properties
If \(a\) and \(b\) are positive numbers and \(n\) is rational, then the following properties are true.
1. \(\ln (1)=0\)
2. \(\ln (ab)=\ln a + \ln b\)
3. \(\ln (a^n)= n \ln a\)
4. \(\ln \left ( \frac{a}{b} \right ) = \ln a - \ln b\)
Proof The first property was already discussed. The proof for the second property follows from the fact that two antiderivatives for the same function differ by a constant. From the Second Fundamental Theorem of Calculus and Definition 5.1.1 yields
- $$\frac{d}{dx} [\ln x]= \frac{d}{dx} \left [ \int_{1}^{x} \frac{1}{t} \:dt \right ] = \frac{1}{x}.$$
Consider the two derivatives
- $$\frac{d}{dx} [\ln x]= \frac{a}{ax} = \frac{1}{x}$$
and
- $$\frac{d}{dx} [\ln a + \ln x ]= 0+ \frac{1}{x} = \frac{1}{x}.$$
Because \(\ln(ax)\) and \((\ln a + \ln x)\) are both antiderivatives for \(1/x\), they must differ at most by a constant.
- \(\ln (ax)= \ln a + \ln x + C\)
By letting \(x=1\) implies that \(C=0\). The third property can be proved similarly by comparing the derivatives for \(\ln( x^n)\) and \(n \ln x\). Finally, using the second and third properties to prove the fouth.
- $$ \ln \left ( \frac{a}{b} \right ) = \ln [a(b^{-1})]=\ln a + \ln(b^{-1})=\ln a - \ln b$$
Example 5.1.1 Expanding Logarithmic Expressions
|
|
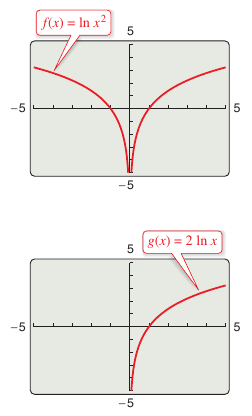
When using logarithmic properties to rewrite logarithmic functions verify that the domain for the rewritten function matches the domain for the original. For example, the domain for \(f(x)= \ln x^2\) is all real numbers except \(x=0\), and the domain for \(g(x)=2 \ln x\) is all positive real numbers, as shown in Figure 5.1.4. |
The Number \(e\)[2]
|
|
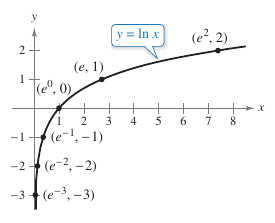
In algebra logarithms are defined with a base number. For example, common logarithms have a base 10 and therefore \(\log_10 10=1\). The base for the natural logarithm is defined by the natural logarithmic function is continuous, is one-to-one, and has a range \((-\infty,\infty)\). Therefore, there must be a unique real number \(x\) such that \(\ln x =1\), as shown in Figure 5.1.5. This number is denoted by the letter \(e\). The \(e\) is irrational and is an infinite expansion that never repeats. It has the following decimal approximation.
|
Definition 5.1.2 \(e\)
The letter \(e\) denotes the positive real number such that
- $$\ln e = \int_{1}^{e} \frac{1}{t}\:dt=1.$$
Definition 5.1.2 and logarithmic properties are used to evaluate natural logarithms for many numbers. For example, by using the property
| \(\ln (x^n)\) | \(=n \ln e\) |
| \(=n(1)\) | |
| \(=n\) |
evaluating \(\ln (e^n)\) for various \(n\)-values as shown in Figure 5.1.6 and Table 5.1.1.
|
|
The logarithms shown in Table 5.1.1 are convenient because the \(x\)-values are integer \(e\) powers. Most logarithmic expressions are best evaluated with a calculator. | |||||||||||||||||||||
Example 5.1.2 Evaluating Natural Logarithmic Expressions
a. \(\ln 2 \approx 0.693\)
b. \(\ln 32 \approx 3.466\)
c. \(\ln 0.1 \approx -2.303\)
Natural Logarithmic Function Derivatives
Theorem 5.1.3 defines the derivative for natural logarithmic functions. Part one follows form Definition 5.1.1. Part two is the Chain Rule applied to part one.
Theorem 5.1.3 Natural Logarithmic Function Derivative
Let \(u\) be a differentiable function for \(x\).
- $$\textbf{1.}\: \frac{d}{dx} [\ln x]=\frac{1}{x}, \:\: x >0$$
- $$\textbf{2.}\: \frac{d}{dx} [\ln u]=\frac{1}{u} \frac{du}{dx}=\frac{{u}'}{u}, \:\: u >0$$
Example 5.1.3 Differentiating Logarithmic Functions
Logarithmic properties simplify calculations involving products, quotients, and powers by turning multiplication into addition and division into subtraction. Then the slide-rule[3] was invented to speed hand-written calculations. Today logarithmic properties are used to simplify differentiating functions with products, quotients, and powers.
Example 5.1.4 Differentiation with Logarithmic Properties, Square Root
Differentiate
- \(f(x)=\ln \sqrt{x=1}.\)
- \(f(x)=\ln \sqrt{x=1}.\)
Solution Because
- $$f(x)=\ln \sqrt{x=1}= \ln(x+1)^{1/2} = \frac{1}{2} \ln (x+1)\:\:\:\:\color{red}{\text{Rewrite before differentiating.}}$$
can be written as
- $${f}'(x) = \frac{1}{2} \left ( \frac{1}{x+1} \right ) = \frac{1}{2(x+1)}\:\:\:\:\color{red}{\text{Differentiate.}}$$
Example 5.1.5 Differentiation with Logarithmic Properties, Quotient
Differentiate
- $$f(x)=\ln \frac{ x(x^2+1)^2}{ \sqrt{2x^3-1}}.$$
Solution Because
|
$$=\ln \frac{ x(x^2+1)^2}{ \sqrt{2x^3-1}}$$ | |
|
$$=\ln x +2 \ln (x^2+1) - \frac{1}{2} \ln (2x^3-1)$$ |
Rewrite before differentiating |
can be written as
|
$$=\frac{1}{x} +2 \left ( \frac{2x}{x^2+1} \right ) - \frac{1}{2} \left ( \frac{6x^2}{2x^3-1} \right )$$ |
Differentiate |
|
$$= \frac{1}{x}+ \frac{4x}{x^2+1}- \frac{3x^2}{2x^3-1}.$$ |
Simplify |
In Examples 5.1.4 and 5.1.5, recognize the benefit from applying logarithmic properties before differentiating. Consider the difficulty in direct differentiation for the function given in Example 5.1.5. On occasion, it is convenient to use logarithms in differentiating non-logarithmic functions. This procedure is called logarithmic differentiation.
Example 5.1.6 Logarithmic Differentiation
Find the derivative for
- $$y=\frac{(-2)^2}{\sqrt{x^2=1}}, \:\:\:\: x \ne 2.$$
Solution Note that \(y>0\) for all \(x \ne 2\). So, \(\ln y\) is defined. Begin by taking the natural logarithm for each side. Then apply logarithmic properties and differentiate implicitly. Then solve for \({y}'\).
Because the natural logarithm is undefined for negative numbers, expressions with the form \(\ln \left | u \right | \). The Theorem 5.1.4 states that functions with the form \(y=\ln \left | u \right | \) can be differentiated as though the absolute value notation was not present.
Theorem 5.1.4 Derivatives Involving Absolute Value
If \(u\) is a differentiable function for \(x\) such that \(u \ne 0\), then
- $$ \frac{d}{dx} [ \ln \left | u \right | ] = \frac{{u}'}{u}.$$
Proof if \(u >0\), then \(\left | u \right | = u\), an the result follows from Theorem 5.1.3. If \(u<0\), then \(\left | u \right | = -u \), produces
|
$$= \frac{d}{dx} [ \ln(-u)]$$ |
|
$$= \frac{-{u}'}{-u}$$ | |
|
$$= \frac{{u}'}{u}.$$ |
Example 5.1.7 Derivative Involving Absolute Value
Find the derivative for
- \(f(x)=\ln \left | \cos x \right |.\)
Solution Using Theorem 5.1.4, let \(u= \cos x\) and write
|
$$=\frac{{u}'}{u}$$ | |
|
$$= \frac{ -\sin x}{ \cos x}$$ |
\(u=\cos x\) | |
|
\(=- \tan x\) |
Simplify |
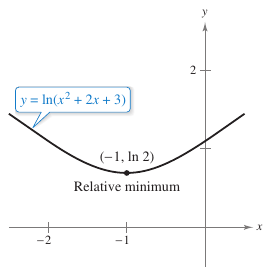
Example 5.1.8 Finding Relative Extrema
|
|
Locate the relative extrema for
Solution Differentiating \(y\) yields
Because \(dy/dy=0\) when \(x = -1\), apply the First Derivative Test and conclude that the point \((-1, \ln 2)\) is a relative minimum. Because there are no other critical points, it follows that this is the only relative extremum, as shown in Figure 5.1.7. |
Internal Links
Parent Article: Calculus I 05 Logarithmic, Exponential, and Other Transcendental Functions