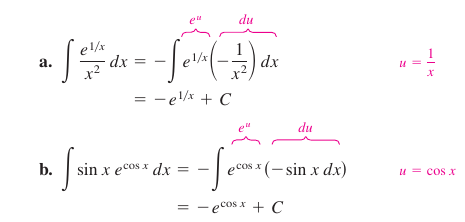Difference between revisions of "Calculus I 05.04 Exponential Functions: Differentiation and Integration"
(→Example 5.4.10 Finding Areas Bounded by Exponential Functions) |
(No difference)
|
Latest revision as of 21:07, 13 December 2020
| Previous | Calculus I 05.03 Inverse Functions |
| Next | Calculus I 05.05 Bases Other than e and Applications |
Contents
5.4 Exponential Functions: Differentiation and Integration
- Natural exponential function properties.
- Differentiate natural exponential functions.
- Integrate natural exponential functions.
The Natural Exponential Function
|
|
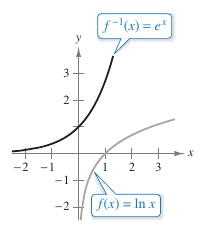
The function \(f(x)=\ln x\) is increasing on its entire domain, and therefore, has an inverse function \(f^{-1}\). The domain for \(f^{-1}\) is the all real number set. The range for \(f^{-1}\) is the all positive real number set. The inverse function for the natural logarithmic function is the natural exponential function, as shown in Figure 5.4.1. This implies, for any real number \(x\),
If \(x\) is rational, then
Because the natural logarithmic function is one-to-one, conclude that \(f^{-1}(x)\) and \(e^x\) agree for rational \(x\)-values. Definition 5.4.1 extends \(e^x\) to include all real \(x\)-values. Definition 5.4.1 The Natural Exponential FunctionThe inverse function for the natural logarithmic function, \(f(x)=\ln x\) is called the natural exponential function and is denoted by
Therefore,
The inverse relationship between the natural logarithmic function and the natural exponential function is summarized as shown below.
|
Example 5.4.1 Solving an Exponential Equation
Solve
- \(7=e^{x+1}\)
Solution Convert from exponential form to logarithmic form by taking the natural logarithm from both sides on the equation.
|
\(=e^{x+1}\) |
Original equation |
|
\(=\ln (e^{x+1})\) |
Take natural logarithm from each side. |
|
\(=x+1\) |
Apply Definition 5.4.1. |
|
\(=x\) |
Solve for \(x\). |
Therefore, the solution is \(-1+\ln 7 \approx -0.946\). Verify the solution as shown below.
|
\(=e^{x+1}\) |
Original equation |
|
\(\stackrel{\text{?}}{=} e^{(\color{red}{-1+\ln 7})+1}\) |
Substitute \(-1+\ln 7\) in original equation. |
|
\(\stackrel{\text{?}}{=} e^{\ln 7}\) |
Simplify. |
|
\(=7\) |
Solution checks. |
Example 5.4.2 Solving a Logarithmic Equation
Solve
- \(\ln (2x-3) = 5.\)
Solution To convert from logarithmic from to exponential form, exponentiate both sides by \(e\).
|
\(=5\) |
Original equation |
|
\(=e^5\) |
Exponentiate each side by \(e\) |
|
\(=e^5\) |
Apply inverse property |
|
\(=\frac{1}{2} (e^5+3)\) |
Solve for \(x\) |
|
\(\approx 75.707\) |
Approximate |
Theorem 5.4.1 Exponential Functions Identities
Let \(a\) and \(b\) be any real numbers.
- \(\textbf{1.}\:\:e^a e^b= e^{a+b}\)
- $$\textbf{2.}\:\:\frac{e^a}{e^b}= e^{a-b}$$
Proof To prove Identity 1, write
- \(\ln (e^a e^b)= \ln (e^a)+\ln (e^b) = a+b= \ln (e^{a+b}.\)
Because the natural logarithmic function is one-to-one, conclude that
- \(e^a e^b= e^{a+b}.\)
The proof for Identity 2 is done in a similar manner.
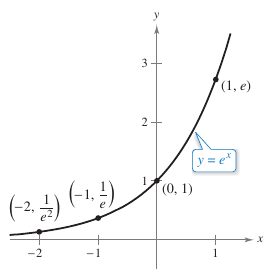
Natural Exponential Function Properties
|
|
1. The domain for \(f(x)=e^x\) is
and the range is
2. The function \(f(x)=e^x\) is continuous, increasing, and one-to-one on its entire domain. |
Exponential Function Derivatives Involving \(e\)
An interesting property about the natural exponential function involving \(e\), is that the function is its own derivative. In other words, the a solution for the differential equation \({y}'=y.\) This result is stated in Theorem 5.4.2.
Theorem 5.4.2 Natural Exponential Function Derivatives
Let \(u\) be a differentiable function for \(x\).
- $$\textbf{1.} \:\: \frac{d}{dx} [e^x]=e^x$$
- $$\textbf{2.} \:\: \frac{d}{dx} [e^u]=e^u\frac{du}{dx}$$
Proof To prove property 1, use the face that \(\ln e^x=x\), and differentiate both sides.
|
\(=x\) |
Exponential Function Definition. |
|
$$=\frac{d}{dx}[x]$$ |
Differentiate each side with respect to x. |
|
$$=1$$ | |
|
$$=e^x$$ |
The proof for Property 2 follow from the Chain Rule.
A geometric interpretation yields the slope for \(f(x)=e^x\)'s graph at any point \((x,e^x)\) equals the \(y\)-coordinate for that point.
Example 5.4.3 Differentiating Exponential Functions
Find the derivative for each function
a. \(y=e^{2x-1}\)
b. \(y=e^{-3/x}\)
Solution
| a. |
$$\frac{d}{dx} \left [ e^{2x-1} \right ]$$ |
$$=e^u\:\frac{du}{dx}$$ |
\(=2e^{2x-1}\) |
\(u=2x-1\) | |
| b. |
$$\frac{d}{dx} \left [ e^{-3/x} \right ]$$ |
$$=e^u\: \frac{du}{dx}$$ |
$$=\left ( \frac{3}{x^2} \right ) e^{-3/x}$$ |
$$=\frac{3 e^{-3/x}}{x^2}$$ |
\(u=-\frac{3}{u}\) |
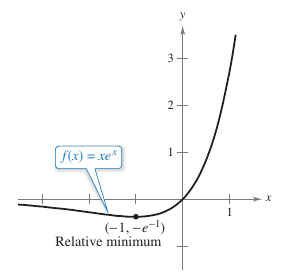
Example 5.4.4 Locating Relative Extrema
|
|
Find the relative extrema for
Solution The derivative for \(f\) is
Because \(e^x\) is never zero, the derivative is zero only when \(x =-1\). By the First Derivative Test, \(x =-1\) is a relative minimum, as shown in Figure 5.4.3. Because the derivative \({f}'(x)=e^x(x+1)\) is defined for all \(x\), there are no other critical points. |
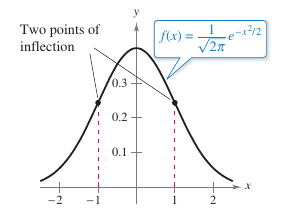
Example 5.4.5 The Standard Normal Probability Density Function
|
|
Show the standard normal probability density function
has inflection points when \(x = \pm 1.\)
The second derivative equals zero when \(x= \pm 1\). Applying differentiation techniques yields two inflection points, as shown in Figure 5.4.4. |
Example 5.4.6 California's Population
The projected population \(y\), in thousands, for California from 2015 through 2030 is modeled by
- \(y=34,696e^{0.0097t}\)
where \(t\) represents the year, with \(t=15\) corresponding to 2015. At what rate will the population bechanging in 2020?
Solution The derivative for the model is
|
\(=(0.0097)(34,696)e^{0.0097t}\) |
|
\( \approx 336.55e^{0.0097t}.\) |
Evaluating the derivative when \(t=20\) yields the change rate in 2020 at about
- 408.6 thousand people per year.
Exponential Function Integrals
Each differentiation formula in Theorem 5.4.2 has a corresponding integration formula.
Theorem 5.4.3 Integration Rules for Exponential Functions
Let \(u\) be a differentiable function for \(x\).
- $$\textbf{1.}\:\: \int e^x\:dx=e^x+C$$
- $$\textbf{2.}\:\: \int e^u\:du=e^u+C$$
Example 5.4.7 Integrating Exponential Functions
Find the indefinite integral
- $$\int e^{3x+1}\:dx$$
Solution Let \(u=3x+1\), then \(du=3\:dx\).
|
$$=\frac{1}{3} \int e^{3x+1} (3) \: dx$$ |
Multiply and divide by three. |
|
$$=\frac{1}{3} \int e^{\color{red}{u}}\: du$$ |
Substitute \(u=3x+1\). | |
|
$$=\frac{1}{3} e^u+C$$ |
Apply Exponential Rule. | |
|
$$=\frac{e^{3x+1}}{3}+C$$ |
Back substitution |
In Example 5.4.7, the missing constant faction three was introduced to create \(du=3\:dx\). However, a missing variable factor cannot be introduced in the integrand. For example,
- $$\int e^{-x^2}\: dx \ne \frac{1}{x} \int e^{-x^2} (x\: dx).$$
Example 5.4.8 Integrating Exponential Functions
Find the indefinite integral
- $$\int 5xe^{-x^2}\:dx$$
Solution Let \(u=-x^2\), then \(du=-2x\), or \(dx=-du/2\).
|
$$=\int 5e^{-x^2}(x\:dx)$$ |
Regroup integrand |
|
$$=\int 5 e^{\color{red}{u}} \left ( -\frac{du}{2} \right )$$ |
Substitute: \(u=-x^2\) | |
|
$$=-\frac{5}{2} \int e^u\:du$$ |
Constant Multiple Rule | |
|
$$=-\frac{5}{2} e^u+C$$ |
Apply Exponential Rule | |
|
$$=-\frac{5}{2} e^{-x^2}+C$$ |
Back substitute |
Example 5.4.9 Integrating Exponential Functions
Find each indefinite integral.
- $$\textbf{a.}\: \int \frac{e^{1/x}}{x^2}\:dx\:\:\:\:\textbf{a.}\: \int \sin x\:e^{\cos x}\:dx$$
Solution
Example 5.4.10 Finding Areas Bounded by Exponential Functions
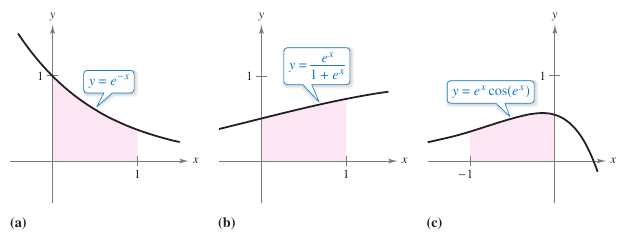
Evaluate each definite integral
- $$\textbf{a.}\:\:\int_{0}^{1} e^{-x}\:dx\:\:\:\:\textbf{b.}\:\:\int_{0}^{1}\frac{e^x}{1+e^x} \textbf{c.}\:\:\int_{-1}^{0} \left [ e^x \cos (e^x)\right ]\:dx$$
Solution
| a. |
$$\int_{0}^{1} e^{-x}\:dx$$ |
$$=\left.\vphantom{ \frac{3}{4} } -e^{-x} \right ]_{0}^{1}$$ |
See Figure 5.4.5(a) |
|
\(=-e^{-1}-(-1)\) | |||
|
$$=1-\frac{1}{e}$$ | |||
|
\(\approx 0.632\) |
| b. |
$$\int_{0}^{1} \frac{e^x}{1+e^x}\:dx$$ |
$$=\left.\vphantom{ \frac{3}{4} } \ln (1+e^{-x}) \right ]_{0}^{1}$$ |
See Figure 5.4.5(b) |
|
\(=\ln(1+e)-\ln 2\) | |||
|
\(\approx 0.620\) |
| c. |
$$\int_{-1}^{0} \left [ e^x \cos (e^x)\right ]\:dx$$ |
$$=\left.\vphantom{ \frac{3}{4} } \sin (e^x) \right ]_{-1}^{0}$$ |
See Figure 5.4.5(c) |
|
\(=\sin 1 - \sin (e^{-1})\) | |||
|
\(\approx 0.482\) |
Internal Links
Parent Article: Calculus I 05 Logarithmic, Exponential, and Other Transcendental Functions