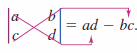Calculus III 11.04 The Cross Product for Two Vectors in Three Dimensions

Previous	Calculus III 11.03 The Dot Product for Two Vectors in Three Dimensions
Next	Calculus III 11.05 Lines and Planes in Three Dimensions

11.4 The Cross Product for Two Vectors in Three Dimensions

• Find the cross product for two vectors in three dimensions.
• Use the triple scalar product for three vectors in three dimensions.

The Cross Product

The Cross Product, or Vector Product, is a function that yields a vector that is orthogonal to two given vectors. It is most conveniently defined and calculated using the standard unit vector form.

Definition 11.4.1 Cross Product for Two Vectors in Three Dimensions

Let

\( \textbf{u}=u_{1}\textbf{i}+u_{2}\textbf{j}+u_{3}\textbf{k} \text{ and } \textbf{v}=v_{1}\textbf{i}+v_{2}\textbf{j}+v_{3}\textbf{k} \)

be vectors in three dimensions. The cross product for \( \textbf{u} \) and \( \textbf{v} \) is the vector

\( \textbf{u} \times \textbf{v} = (u_{2}v_{3}-u_{3}v_{2})\textbf{i}- (u_{1}v_{3}-u_{3}v_{1})\textbf{j} - (u_{1}v_{2}-u_{2}v_{1} )\textbf{k}\)

The cross product is not defined for vectors in two dimensions.

The determinant form with cofactor expansion can be used to calculate the cross product as shown in Figure 11.4.1 below. (This determinant form is used simply to help remember the formula for the cross product—it is technically not a determinant because not all the matrix entries are real numbers.)

Figure 11.4.1

Note the minus sign leading the \(\textbf{j}\)-component. Each \(2 \times 2\) determinants can be evaluated by using the diagonal pattern shown in Figure 11.4.2.

Figure 11.4.2

Here are two examples,

$$ \begin{vmatrix} 2 & 4 \\ 3 & -1 \\ \end{vmatrix} = (2)(-1)-(4)(3)=-2-12=-14$$

and

$$ \begin{vmatrix} 4 & 0 \\ -6 & 3 \\ \end{vmatrix} = (4)(3)-(0)(-6)=12$$

Example 11.4.1 Finding the Cross Product

For \( \textbf{u}= \textbf{i} -2\textbf{j}+\textbf{k} \) and \( \textbf{v}=3\textbf{i}+\textbf{j}-2\textbf{k} \), find the following.
a. \( \textbf{u} \times \textbf{v} \)
b. \( \textbf{v} \times \textbf{u} \)
c. \( \textbf{v} \times \textbf{v} \)
Solution
a.

$$ \textbf{u} \times \textbf{v} $$	$$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 1 & -2 & 1 \\ 3 & 1 & -2 \end{vmatrix} $$
	\(= \begin{vmatrix} -2 & 1 \\ 1 & -2 \end{vmatrix} \textbf{i} - \begin{vmatrix} 1 & 1 \\ 3 & -2 \end{vmatrix} \textbf{j} + \begin{vmatrix} 1 & -2 \\ 3 & 1 \end{vmatrix} \textbf{k} \)
	\(= (4-1)\textbf{i} -(-2-3)\textbf{j}+(1+6)\textbf{k} \)
	\(= 3\textbf{i} + 5\textbf{j}+7\textbf{k} \)

b.

$$ \textbf{v} \times \textbf{u} $$	$$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 3 & 1 & -2 \\ 1 & -2 & 1 \end{vmatrix} $$
	\(= \begin{vmatrix} 1 & -2 \\ -2 & 1 \end{vmatrix} \textbf{i} - \begin{vmatrix} 3 & -2 \\ 1 & 1 \end{vmatrix} \textbf{j} + \begin{vmatrix} 3 & 1 \\ 1 & -2 \end{vmatrix} \textbf{k} \)
	\(= (1-4)\textbf{i} -(3+2)\textbf{j}+(-6-1)\textbf{k} \)
	\(= -3\textbf{i} - 5\textbf{j} - 7\textbf{k} \)

c.

$$ \textbf{v} \times \textbf{v} $$

$$= \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 3 & 1 & -2 \\ 3 & 1 & -2 \end{vmatrix} = 0 $$

Theorem 11.4.1 Algebraic Properties for the Cross Product

Let \( \textbf{u} \), \( \textbf{v} \), and \( \textbf{w} \) be vectors in three dimensions. Let \(c\) be a scalar.

1. \( \textbf{u} \times \textbf{v} = - (\textbf{v} \times \textbf{u}) \)
2. \( \textbf{u} \times (\textbf{v} + \textbf{w}) = (\textbf{u} \times \textbf{v}) + (\textbf{u} \times \textbf{w}) \)
3. \( c(\textbf{u} \times \textbf{v}) = (c\textbf{u}) \times \textbf{v}) = \textbf{u} \times (c\textbf{v}) \)
4. \( \textbf{u} \times \textbf{0} = \textbf{0} \times \textbf{u} = \textbf{0} \)
5. \( \textbf{u} \times \textbf{u} = \textbf{0} \)
6. \( \textbf{u} \cdot ( \textbf{v} \times \textbf{w}) = (\textbf{u} \times \textbf{v}) \cdot \textbf{w} \)

Proof To prove Property 1, let \( \textbf{u}= u_{1}\textbf{i} +u_{2}\textbf{j}+u_{3}\textbf{k} \) and \( \textbf{v}= v_{1}\textbf{i} +v_{2}\textbf{j}+v_{3}\textbf{k} \). This yields,

\( \textbf{u} \times \textbf{v} = (u_{2}v_{3} - u_{3}v_{2})\textbf{i} +(u_{1}v_{3} - u_{3}v_{1})\textbf{j}+(u_{1}v_{2} - u_{2}v_{1})\textbf{k} \)

and

\( \textbf{v} \times \textbf{u} = (v_{2}u_{3} - v_{3}u_{2})\textbf{i} - (v_{1}u_{3} - v_{3}u_{1})\textbf{j}+(v_{1}u_{2} - v_{2}u_{1})\textbf{k} \)

which implies that \( \textbf{u} \times \textbf{v} = - (\textbf{v} \times \textbf{u}) \).
Note that Property 1 is not commutative. Instead \( \textbf{u} \times \textbf{v} \) and \(\textbf{v} \times \textbf{u} \) have the same length but opposite directions.

Theorem 11.4.2 Geometric Properties for the Cross Product

The vectors \( \textbf{u} \) and \( \textbf{v} \) form adjacent sides on a parallelogram. Figure 11.4.3

Let \( \textbf{u} \) and \( \textbf{v} \) be nonzero vectors in three dimensions. Let \(\theta\) be the angle between \( \textbf{u} \) and \( \textbf{v} \). \( \textbf{u} \times \textbf{v} \) is orthogonal to both \( \textbf{u} \) and \( \textbf{v} \). \( \| \textbf{u} \times \textbf{v} \| = \| \textbf{u} \| \| \textbf{v} \| \sin \theta \) \( \textbf{u} \times \textbf{v} = 0 \) if and only if \( \textbf{u} \) and \( \textbf{v} \) are scalar multiples for each other. \( \| \textbf{u} \times \textbf{v} \| = \) area for a parallelogram having \( \textbf{u} \) and \( \textbf{v} \) as adjacent sides. It follows from Properties 1 and 2 that if \( \textbf{n} \) is a unit vector orthogonal to both \( \textbf{u} \) and \( \textbf{v} \). then \( \textbf{u} \times \textbf{v} = \pm (\| \textbf{u} \| \| \textbf{v} \| \sin \theta ) \textbf{n} \) Proof To prove Property 2, note that because \( \cos \theta = (\textbf{u} \cdot \textbf{v})/( \|\textbf{u} \| \| \textbf{v} \|) \), it follows that \( \| \textbf{u} \| \| \textbf{v} \| \sin \theta \) \(= \| \textbf{u} \| \| \textbf{v} \| \sqrt{1- \cos^{2} \theta } \) $$= \| \textbf{u} \| \| \textbf{v} \| \sqrt{1- \frac{(\textbf{u} \cdot \textbf{v})}{ \|\textbf{u}\|^{2} \|\textbf{v} \|^{2}} } $$ \(= \sqrt{ \|\textbf{u}\|^{2} \|\textbf{v} \|^{2} - (\textbf{u} \cdot \textbf{v})^{2} }\) \(= \sqrt{ ( (u_{1})^{2} + (u_{2})^{2} + (u_{3})^{2}) + ( (v_{1})^{2} + (v_{2})^{2} + (v_{3})^{2}) - (u_{1}v_{1} + u_{2}v_{2} + u_{3}v_{3})^{2} } \) \(= \sqrt{ ( u_{2}v_{3} - u_{3}v_{2} )^{2} + ( u_{1}v_{3} - u_{3}v_{1})^{2} + (u_{1}v_{2} - u_{2}v_{1})^{2} } \) \( = \| \textbf{u} \times \textbf{v} \| \) 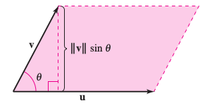To prove Property 4, refer to Figure 11.4.3. It shows a parallelogram with \( \textbf{u} \) and \( \textbf{v} \) as adjacent sides. Because the height is \( \| \textbf{v} \| \sin \theta \), the area is Area (base)(height) \(= \|\textbf{u}\| \| \textbf{v} \| \sin \theta \) \(= \| \textbf{u} \times \textbf{v} \| \)

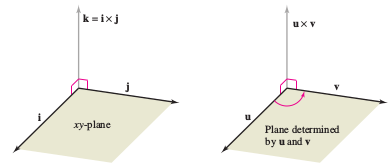
Both \( \textbf{u} \times \textbf{v} \) and \( \textbf{v} \times \textbf{u} \) are perpendicular to the plane determined by \( \textbf{u} \) and \( \textbf{v} \). One way to remember the orientations for vectors \( \textbf{u} \), \( \textbf{v} \), and \( \textbf{u} \times \textbf{v} \) is to compare them with the unit vectors \( \textbf{i} \), \( \textbf{j} \), and \( \textbf{k}= \textbf{i} \times \textbf{j} \), as shown in Figure 11.4.3. The three vectors \( \textbf{u} \), \( \textbf{v} \), and \( \textbf{u} \times \textbf{v} \) form a right-handed system, whereas the three vectors \( \textbf{u} \), \( \textbf{v} \), and \( \textbf{v} \times \textbf{u} \) form a left-handed system.

Right-handed systems.
Figure 11.4.4

Example 11.4.2 Using the Cross Product

The vector \( \textbf{u} \times \textbf{v} \) is orthogonal to both \( \textbf{u} \) and \( \textbf{v} \). Figure 11.4.5

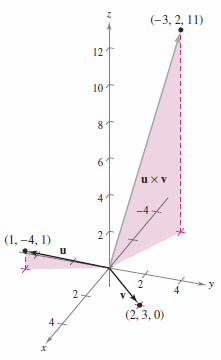
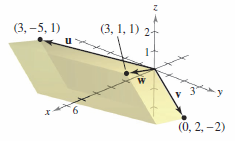
Find a unit vector that is orthogonal to both \( \textbf{u}= \textbf{i} -4\textbf{j}+\textbf{k} \) and \( \textbf{v}= 2\textbf{i}+3\textbf{j} \) Solution The cross product \( \textbf{u} \times \textbf{v} \), as show in Figure 11.4.5, is orthogonal to both \( \textbf{u} \) and \( \textbf{v} \). $$ \textbf{u} \times \textbf{v} = \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 1 & -4 & 1 \\ 2 & 3 & 0 \end{vmatrix} \:\:\:\:\color{red}{\text{Cross Product}}$$ Because \(\| \textbf{u} \times \textbf{v} \| = \sqrt{ (-3)^{2} + 2^{2} + 11^{2} } = \sqrt{134} \) a unit vector orthogonal to both \( \textbf{u} \) and \( \textbf{v} \) is $$ \frac{ \textbf{u} \times \textbf{v} }{ \| \textbf{u} \times \textbf{v} \| }= - \frac{3}{\sqrt{134}}\textbf{i} +\frac{2}{\sqrt{134}} \textbf{j} +\frac{11}{\sqrt{134}} \textbf{k}$$ Using \( \textbf{u} \times \textbf{v} \) would produce the same answer, but as a negative vector.

Example 11.4.3 Geometric Application for the Cross Product

The parallelogram has an area \(\approx \) 32.19. Figure 11.4.6

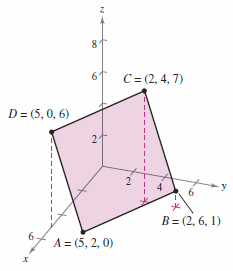
Show the quadrilateral is a parallelogram and find its area using the vertices listed. \(A\) \(=(5,2,0) \) \(B\) \(=(2,6,1) \) \(C\) \(=(2,4,7) \) \(D\) \(=(5,0,6) \) Solution The parallelogram in Figure 11.4.6 has sides corresponding to four vectors. \(\overrightarrow{AB}\) \(= -3\textbf{i}+4\textbf{j} +\textbf{k} \) \(\:\:\:\:\overrightarrow{CD}\) \(=3\textbf{i}-4\textbf{j} -\textbf{k} \) \( = - \overrightarrow{AB}\) \(\overrightarrow{AD}\) \(= 0\textbf{i}-2\textbf{j} +6\textbf{k} \) \(\:\:\:\:\overrightarrow{CB}\) \(= 0\textbf{i}+2\textbf{j} -6\textbf{k} \) \(= -\overrightarrow{AD} \) This makes \(\overrightarrow{AB}\) parallel to \(\overrightarrow{CD}\) and \(\overrightarrow{AD}\) parallel to \(\overrightarrow{CB}\). Therefore the quadrilateral is a parallelogram with \(\overrightarrow{AB}\) and \(\overrightarrow{AD}\) as adjacent sides. The area is found by using the cross product. $$ \overrightarrow{AB} \times \overrightarrow{AD} = \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ -3 & 4 & 1 \\ 0 & -2 & 6 \end{vmatrix} = 26\textbf{i}+18\textbf{j} +6\textbf{k} $$ Taking the absolute value yields \( \| \overrightarrow{AB} \times \overrightarrow{AD} \| = \sqrt{ 1036 } \approx 32.19 \) Challenge Question: Is the parallelogram a rectangle?

Example 11.4.4 An Application for the Cross Product

The moment for \( \textbf{F} \) about \(P\) Figure 11.4.7 A 50 pound vertical force is applied at point \(Q\). Figure 11.4.8

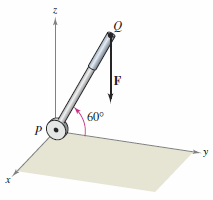
A 50 pound force is applied to a one-foot long lever that is attached to an axle at point \(P\), as shown in figure 11.4.7. Find the moment for this force about the point \(P\) when \(\theta=60^{\circ}\). Solution The cross product can be used to measure torque - the moment M for a force F about a point P, as shown in Figure 11.4.8. 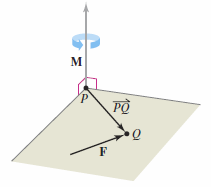If the point the force is applied to is \(Q\), then the moment for F' about \(P\) is \( \textbf{M} = \overrightarrow{PQ} \times \textbf{F}\:\:\:\: \color{red}{ \text{ Moment for F about }P} \) The variable \( \textbf{M} \)'s magnitude measures the tendency for the vector \( \overrightarrow{PQ} \) to rotate counterclockwise (using the right-hand rule) about an axis directed along the vector \( \textbf{M} \). Using this the 50-pound force can be represented as \( \textbf{F} = -50 \textbf{k} \) and the lever as $$ \overrightarrow{PQ} = \cos ( 60^{\circ} ) \textbf{j} + \sin( 60^{\circ} ) \textbf{j} = \frac{1}{2}\textbf{j} + \frac{ \sqrt{3} }{2} \textbf{k}. $$ The moment for \( \textbf{F} \) about \( P \) is $$ \textbf{M}= \overrightarrow{PQ} \times \textbf{F} = \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 0 & \frac{1}{2} & \frac{\sqrt{3}}{2} \\ 0 & 0 & -50 \end{vmatrix} = -25\textbf{i} \:\:\:\: \color{red}{ \text{ Moment for F about }P} $$ The magnitude for this moment is 25 foot-pounds. Note the moment (the tendency for the lever to rotate about its axle) is dependent on the angle \( \theta \). When \( \theta = \pi /2 \), the moment is zero. The moment is greatest when \( \theta = 0\).

The Triple Scalar Product

For vectors \( \textbf{u} \), \( \textbf{v} \), and \( \textbf{w} \) in three dimensions, the dot product for

\( \textbf{u} \cdot ( \textbf{v} \times \textbf{w}) \)

is called the triple scalar product as defined in Theorem 11.4.3.

Theorem 11.4.3 The Triple Scalar Product

For \(\textbf{u}=u_{1}\textbf{i}+u_{2}\textbf{j}+u_{3}\textbf{k} \), \( \textbf{v}=v_{1}\textbf{i}+v_{2}\textbf{j}+v_{3}\textbf{k} \), and \( \textbf{w}=w_{1}\textbf{i}+w_{2}\textbf{j}+w_{3}\textbf{k} \), the triple scalar product is

$$ \textbf{u} \cdot ( \textbf{v} \times \textbf{w}) = \begin{vmatrix} u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \\ w_{1} & w_{2} & w_{3} \end{vmatrix}. $$

Note that the value for a determinant is multiplied by -1 when any two rows are interchanged. After two such interchanges, the determinant will be unchanged. Therefore, the following triple scalar products are equivalent.

\( \textbf{u} \cdot ( \textbf{v} \times \textbf{w}) = \textbf{v} \cdot ( \textbf{w} \times \textbf{u}) = \textbf{w} \cdot ( \textbf{u} \times \textbf{v}) \)

Challenge Question: Prove the theorem.

Theorem 11.4.4 Geometric Property for the Triple Scalar Product

Base Area \(= \| \textbf{v} \times \textbf{w} \| \) Parallelepiped Volume \(= | \textbf{u} \cdot ( \textbf{v} \times \textbf{w}) | \) Figure 11.4.9

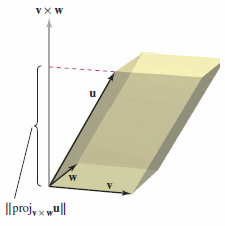
If the vectors \( \textbf{u} \), \( \textbf{v} \), and \( \textbf{w} \) do not lie on the same plane, then the triple scalar product \( \textbf{u} \cdot ( \textbf{v} \times \textbf{w}) \) can be used to determine the volume for the parallelepiped - a polyhedron, where all faces are parallelograms - with \( \textbf{u} \), \( \textbf{v} \), and \( \textbf{w} \) as adjacent edges, as shown in Figure 11.4.9. The volume \(V\) for a parallelepiped with vectors \( \textbf{u} \), \( \textbf{v} \), and \( \textbf{w} \) as adjacent edges is \( V = | \textbf{u} \cdot ( \textbf{v} \times \textbf{w}) | . \) Proof The base area is \( \| \textbf{v} \times \textbf{w} \| \) and the parallelepiped's height is \( \|\text{proj}_{\textbf{v} \times \textbf{w}} \textbf{u} \| \), as shown in Figure 11.4.9. This yields, \(V\) \(= \|\text{proj}_{\textbf{v} \times \textbf{w}} \textbf{u} \| \| \textbf{v} \times \textbf{w} \| \) $$= \left | \frac{\textbf{u} \cdot ( \textbf{v} \times \textbf{w})}{\| \textbf{v} \times \textbf{w} \|} \right | \| \textbf{v} \times \textbf{w} \| $$ \(= | \textbf{u} \cdot ( \textbf{v} \times \textbf{w}) | \). The parallelepiped's volume is 0 if and only if the three vectors are coplanar. This occurs whent the vectors \( \textbf{u} = \langle u_{1},u_{2},u_{3} \rangle \), \( \textbf{v} = \langle u_{1},v_{2},v_{3} \rangle \), and \( \textbf{w} = \langle w_{1},w_{2},w_{3} \rangle \) have the same initial point, they lie in the same plane if and only if $$ \textbf{u} \cdot ( \textbf{v} \times \textbf{w}) = \begin{vmatrix} u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \\ w_{1} & w_{2} & w_{3} \end{vmatrix} = 0 $$

Example 11.4.5 Volume by the Triple Scalar Product

Volume = 36 Figure 11.4.10

Find the parallelepiped's volume shown in Figure 11.4.10. With the following vectors as adjacent edges: \(\textbf{u}= 3\textbf{i}-5\textbf{j}+\textbf{k} \) \(\textbf{v}= 2\textbf{j}-2\textbf{k} \) \(\textbf{w}= 3\textbf{i}+\textbf{j}+\textbf{k} \) Solution By Theorem 11.4.4, \(V\) \(= | \textbf{u} \cdot ( \textbf{v} \times \textbf{w}) |\)    Triple scalar product $$= \begin{vmatrix} 3 & -5 & 1 \\ 0 & 2 & -2 \\ 3 & 1 & 1\end{vmatrix} $$ $$= 3\begin{vmatrix} 2 & -2 \\ 1 & 1 \end{vmatrix} - (-5)\begin{vmatrix} 0 & -2 \\ 3 & 1 \end{vmatrix}+(1)\begin{vmatrix} 0 & 2 \\ 3 & 1 \end{vmatrix} $$ \( = 3(4)+5(6)+1(-6) \) \( = 36 \)

Internal Links

Parent Article: Calculus III 11 Vectors and Spacial Geometry