Calculus III 15.06 Surface Integrals

Previous	Calculus III 15.05 Parametric Surfaces
Next	Calculus III 15.07 Divergence Theorem

15.6 Surface Integrals

• Evaluate a surface integral as a double integral.
• Evaluate a surface integral for a parametric surface.
• Determine the orientation for a surface.
• Understand a flux integral.

Surface Integrals

Figure 15.6.1

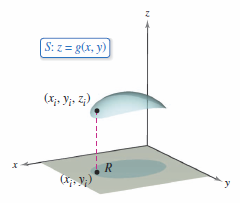
Surface integrals give by \(z=g(x,y)\) are discussed first with the parametric form discussed later on. Let \(S\) be a surface given by \(z=g(x,y)\) and let \(R\) be its projection onto the \(xy\)-plane, as shown in Figure 15.6.1. Let \(g\), \(g_{x}\), and \(g_{y}\) be continuous at all points in \(R\) and let \(f\) be a scalar function defined on \(S\). Recall from Section 14.5 the formula for surface area extends to three dimensions producing the sum $$ \sum_{i=1}^{n} f(x_{i},y_{i},z_{i}) \Delta S_{i} $$ where \( \Delta S_{i} \approx \sqrt{1+[g_{x}(x_{i},y_{i})]^{2} +[g_{y}(x_{i},y_{i})]^{2}} \Delta A_{i}.\) Provided the sum's limit as \(\| \Delta \| \) approaches zero exists, the surface integral for \(f\) over \(S\) is defined as $$ \int_{S} \int f(x,y,z) \: dS = \lim_{\| \Delta\| \rightarrow 0} \sum_{i=1}^{n} f(x_{i},y_{i},z_{i}) \Delta S_{i}.$$ This integral can be evaluated by a double integral.

Theorem 15.6.1 Evaluating a Surface Integral

Let \(S\) be a surface given by \(z=g(x,y)\) and let \(R\) be its projection onto the \(xy\)-plane. If \(g\), \(g_{x}\), and \(g_{y}\) are continuous on \(R\) and \(f\) is continuous on \(S\), then the surface integral for \(f\) over \(S\) is

$$ \int_{S} \int f(x,y,z) \: dS = \int_{R} \int f(x,y,g(x,y)) \sqrt{1+[g_{x}(x,y)]^{2} +[g_{y}(x,y)]^{2}} \: d A.$$

For surfaces described by functions for \(x\) and \(z\), or \(y\) and \(z\). If \(S\) is the graph for \(y=g(x,z)\) and \(R\) is its projection onto the \(xz\)-plane, then

$$ \int_{S} \int f(x,y,z) \: dS = \int_{R} \int f(x,g(x,z),z) \sqrt{1+[g_{x}(x,z)]^{2} +[g_{z}(x,z)]^{2}} \: d A.$$

If \(S\) is the graph for \(x=g(y,z)\) and \(R\) is its projection onto the \(yz\)-plane, then

$$ \int_{S} \int f(x,y,z) \: dS = \int_{R} \int f(g(y,z),y,z) \sqrt{1+[g_{y}(y,z)]^{2} +[g_{z}(y,z)]^{2}} \: d A.$$

If \(f(x,y,z)=1\) the surface integral over \(S\) yields the surface area for \(S\). For example, let the surface \(S\) be the plane given by \(z=x\), where \(0 \leqslant x \leqslant 1\) and \(0 \leqslant y \leqslant 1\). The surface area for \(S\) is \(\sqrt{2}\) square units. Try verifying that

$$ \int_{S} \int f(x,y,z) \: dS = \sqrt{2}.$$

Example 15.6.1 Evaluating a Flat Surface Integral

Figure 15.6.2

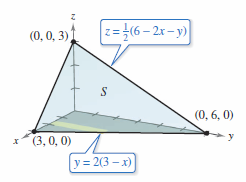
Evaluate the surface integral $$ \int_{S} \int (y^{2}+2yz) \: dS$$ where \(S\) is the first-octant portion for the plane \(2x+y+2z=6.\) Solution Begin by writing \(S\) as \(z\) $$=\frac{1}{2} (6-2x-y) $$ \(g(x,y)\) $$=\frac{1}{2}(6-2x-y). $$ Using the partial derivatives \(g_{x}(x,y) = -1\) and \(g_{y}(x,y) = -\frac{1}{2}\) produces $$\sqrt{1+[g_{x}(x,y)]^{2} +[g_{y}(x,y)]^{2}} = \sqrt{1+1+ \frac{1}{4}} = \frac{3}{2}. $$ Applying the graph in Figure 15.6.2 and Theorem 15.6.1 produces $$\int_{S} \int (y^{2}+2yz) \: dS$$ $$=\int_{R} \int f(x,y,g(x,y)) \sqrt{1+[g_{x}(x,y)]^{2} +[g_{y}(x,y)]^{2}} \: d A $$ $$=\int_{R} \int \left[ y^{2} +2y \left( \frac{1}{2} \right)(6-2x-y) \right]\left( \frac{3}{2} \right) \: d A$$ $$= 3 \int_{0}^{3} \int_{0}^{2(3-x)} y(3-x) \: dy \: dx$$ $$=6 \int_{0}^{3} (3-x)^{3} \: dx $$ $$= \left. -\frac{3}{2} (3-x)^{4} \right]_{0}^{3} = \frac{243}{2}. $$

Figure 15.6.3

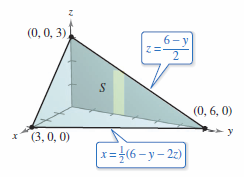
If \(S\) is projected onto the \(yz\)-plane, as shown in Figure 15.6.3, produces \(x=\frac{1}{2}(6-y-2z)\), and $$\sqrt{1+[g_{y}(y,z)]^{2} +[g_{z}(y,z)]^{2}} = \sqrt{1+\frac{1}{4}+1} = \frac{3}{2}.$$ The surface integral is $$\int_{S} \int (y^{2}+2yz) \: dS$$ $$=\int_{R} \int f(g(x,y),y,z) \sqrt{1+[g_{y}(y,z)]^{2} +[g_{z}(y,z)]^{2}} \: d A $$ $$= 3 \int_{0}^{6} \int_{0}^{(6-y)/2} (y^{2}+2yz)\left( \frac{3}{2} \right) \: dz \: dy$$ $$=\frac{3}{8} \int_{0}^{6} (36y-y^{3}) \: dy = \frac{243}{2}. $$ The same principle applies to the \(xz\)-plane.

Example 15.6.2 Evaluating a Cylindrical Surface Integral

Figure 15.6.4

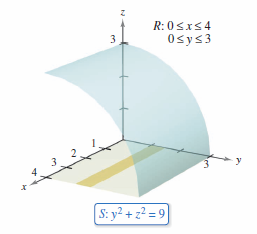
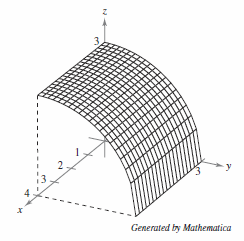
Evaluate the surface integral $$ \int_{S} \int (x+z) \: dS$$ where \(S\) is the first-octant portion for the cylinder \(y^{2}+z^{2}=9\) between \(x=0\) and \(x=4\), as shown in Figure 15.6.4. Solution Project \(S\) onto the \(xy\)-plane such that \(z=g(x,y)= \sqrt{9-y^{2}}\) which produces \( \sqrt{1+[g_{x}(x,y)]^{2} +[g_{y}(x,y)]^{2}}\) $$=\sqrt{1+ \left( \frac{-y}{\sqrt{9-y^{2}}}\right)^{2}} $$ $$= \frac{3}{\sqrt{9-y^{2}}}.$$ Theorem 15.6.1 does not apply directly because \(g_{y}\) is not continuous when \(y=3\). But it does apply for \(0\leqslant b < 3\) with the limit as \(b\) approaches 3, as follows. $$\int_{S} \int (x+z) \: dS$$ $$= \lim_{b \rightarrow 3^{-}} \int_{0}^{b} \int_{0}^{4} \left(x+\sqrt{9-y^{2}} \right) \left(\frac{3}{\sqrt{9-y^{2}}} \right) \: dx \:dy$$ $$=\lim_{b \rightarrow 3^{-}} 3 \int_{0}^{b} \int_{0}^{4} \left( \frac{x}{\sqrt{9-y^{2}}} +1\right) \: dx \:dy $$ $$= \lim_{b \rightarrow 3^{-}} 3 \int_{0}^{b} \left. \frac{x^{2}}{2\sqrt{9-y^{2}}} + x \right]_{0}^{4} \:dy$$ $$=\lim_{b \rightarrow 3^{-}} 3 \int_{0}^{b} \left( \frac{8}{\sqrt{9-y^{2}}} + 4 \right) \:dy$$ $$=\lim_{b \rightarrow 3^{-}} \left[ \vphantom{\frac{1}{2}} 4y+8 \arcsin \frac{y}{3} \right]_{0}^{b}$$ $$= \lim_{b \rightarrow 3^{-}} 3 \left( \vphantom{\frac{1}{2}} 4b+8 \arcsin \frac{b}{3} \right) = 36+24 \left( \frac{\pi}{2} \right)=36+12 \pi$$

The function \(f\) defined on the surface \(S\) is simply \(f(x,y,z)=1\), the surface integral yields the surface area for \(S\),

$$\text{Surface Area }=\int_{S} \int 1 \:dS.$$

When \(S\) is a lamina with variable density and \(\rho(x,y,z)\) is the density at the point \((x,y,z)\), then the mass for the lamina given by

$$\text{Lamina Mass }=\int_{S} \int \rho(x,y,z) \:dS.$$

Example 15.6.3 Finding the Mass for a Surface Lamina

Figure 15.6.5

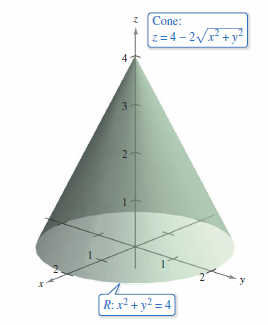
A cone-shaped surface lamina \(S\) is given by \(z=4-2\sqrt{x^{2}+y^{2}}\text{, }0 \leqslant z \leqslant 4\) as shown in Figure 15.6.5. At each point on \(S\), the density is proportional to the distance between the point and the \(z\)-axis. Find the mass \(m\) for the lamina. Solution Projecting \(S\) onto the \(xy\)-plane produces \(S: \: z=4-2 \sqrt{x^{2}+y^{2}} = g(x,y), \: \text{, }0 \leqslant z \leqslant 4\) \(R: \: x^{2}+y^{2} \leqslant 4\) with a density for \(\rho(x,y,z)=k \sqrt{x^{2}+y^{2}}\). Applying a surface integral produces the mass as \(m\) $$= \int_{S} \int \rho(x,y,z) \:dS $$ $$= \int_{R} \int k \sqrt{x^{2}+y^{2}} \sqrt{1+[g_{x}(x,y)]^{2} +[g_{y}(x,y)]^{2}} \: d A$$ $$= k\int_{R} \int \sqrt{x^{2}+y^{2}} \sqrt{1+\frac{4x^{2}}{x^{2}+y^{2}} +\frac{4y^{2}}{x^{2}+y^{2}}} \: d A$$ $$= k\int_{R}\int \sqrt{5} \sqrt{x^{2}+y^{2}} \: d A $$ $$= k \int_{0}^{2 \pi} \int_{0}^{2} (\sqrt{5})r \: dr \: d\theta \:\:\:\: \color{red}{ \text{Convert to Polar Coordinates }}$$ $$= \left.\frac{\sqrt{5}k}{3} \int_{0}^{2 \pi} r^{3} \right]_{0}^{2} \: d\theta $$ $$= \frac{8\sqrt{5}k}{3} \int_{0}^{2 \pi} \: d\theta $$ $$= \frac{8\sqrt{5}k}{3}\left[ \vphantom{\frac{1}{2}} \theta \right]_{0}^{2 \pi} = \frac{16\sqrt{5}k\pi}{3}.$$

Parametric Surfaces and Surface Integrals

For a surface \(S\) given by the vector-valued function

\(\textbf{r}(u,v)=x(u,v)\textbf{i} +y(u,v)\textbf{j} +z(u,v)\textbf{k} \)    Parametric surface

defined over a region \(D\) in the \(uv\)-plane. The surface integral for \(f(x,y,z)\) over \(S\) is given by

$$ \int_{S} \int f(x,y,z) \: dS = \int_{D} \int f(x(u,v),y(u,v),z(u,v))\|\textbf{r}_{u} (u,v)\times \textbf{r}_{v}(u,v) \| \: dA.$$

Note the similarity to a line integral over a space curve \(C\).

$$ \int_{C} f(x,y,z) \: dS = \int_{a}^{b} f(x(t),y(t),z(t))\|\textbf{r}^{\prime}(t) \| \: dt$$

Line integral

Note that \(ds\) and \(dS\) can be expressed as

\(ds=\|\textbf{r}^{\prime}(t) \| \: dt\) and \(dS=\|\textbf{r}_{u} (u,v)\times \textbf{r}_{v}(u,v) \| \: dA.\)

Example 15.6.4 Evaluating a Surface Integral

Figure 15.6.6

Example 15.6.2 demonstrated a surface integral evaluation $$ \int_{S} \int (x+z) \:dS$$ where \(S\) is the first-octant portion for the cylinder \(y^{2}+z^{2}=9\) between \(x=0\) and \(x=4\), as shown in Figure 15.6.6. Reevaluate this integral in parametric form. Solution The surface integral is expressed in parametric form as, \(\textbf{r}(x,\theta)=x\textbf{i} +3 \cos \theta \textbf{j} + 3 \sin \theta \textbf{k}\) where \(0 \leqslant x \leqslant 4 \) and \(0 \leqslant \theta \leqslant \pi/2\). Begin the evaluation by calculating \(\textbf{r}_{x} \) \(=\textbf{i}, \) \(\textbf{r}_{\theta} \) \(= -3 \sin \theta \textbf{j} + 3 \cos \theta \textbf{k}, \) \(\textbf{r}_{x}\times \textbf{r}_{v} \) $$= \begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\ 1 & 0 & 0 \\ 0 & -3 \sin \theta & 3 \cos \theta\end{vmatrix}$$ \(= -3 \cos \theta \textbf{j} - 3 \sin \theta \textbf{k},\) and \(\|\textbf{r}_{x}\times \textbf{r}_{v}\| \) \(= \sqrt{9 \cos^{2} \theta + 9 \sin^{2} \theta} = 3.\) Substituting these into the surface integral produces $$ \int_{D} \int (x+3 \sin \theta)3 \:dA$$ $$= \int_{0}^{4} \int_{0}^{\pi/2} (3x+9 \sin \theta) \:d \theta \: dx$$ $$= \int_{0}^{4} \left[\vphantom{\frac{1}{2}} 3x\theta - 9 \cos \theta \right]_{0}^{\pi/2} \: dx$$ $$= \int_{0}^{4} \left( \vphantom{\frac{1}{2}} \frac{3\pi}{2}x + 9 \right) \: dx$$ $$= \left[\vphantom{\frac{1}{2}} \frac{3\pi}{4}x^{2} + 9x \right]_{0}^{4} = 12\pi+36$$

Surface Orientation

Figure 15.6.7 Figure 15.6.8

Unit normal vectors are used to induce an orientation to a surface \(S\) in space. A surface is orientable when a unit normal vector \(\textbf{N}\) can be defined at every non-boundary point for \(S\) in such a way that the normal vectors vary continuously over the surface \(S\). The surface \(S\) is called an oriented surface. An orientable surface \(S\) has two distinct sides where each side is described by one unit normal vector. For a closed surface, such as a sphere, it is customary to choose the unit normal vector \(\text{N}\) that points outward from the closed surface. Most common surfaces, such as spheres, paraboloids, ellipses, and planes, are orientable. A Möbius Strip[1] is not orientable because one surfaces points outwards in every direction, as shown in Figure 15.6.8. The gradient vector for an orientable surface provides a convenient way to find a unit normal vector. That is, for an orientable surface given by \(z=g(x,y) \:\:\:\: \color{red}{ \text{Orientable surface}} \) let \(G(x,y,z) = z-g(x,y). 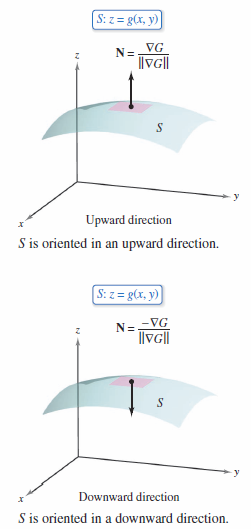\) The surface \(S\) can be oriented outward by making the unit normal vector positive, or inward by making it negative, \(\text{N}\) $$=\frac{\nabla G(x,y,z)}{\|\nabla G(x,y,z)\|} $$ $$=\frac{-g_{x}(x,y)\textbf{i} -g_{y}(x,y)\textbf{j} + \textbf{k} }{\sqrt{1+[g_{x}(x,y)]^{2}+[g_{y}(x,y)]^{2}}} \:\:\:\: \color{red}{ \text{Positive Upward unit normal vector}}$$ and \(\text{N}\) $$=\frac{-\nabla G(x,y,z)}{\|\nabla G(x,y,z)\|} $$ $$=\frac{g_{x}(x,y)\textbf{i} +g_{y}(x,y)\textbf{j} - \textbf{k} }{\sqrt{1+[g_{x}(x,y)]^{2}+[g_{y}(x,y)]^{2}}} \:\:\:\: \color{red}{ \text{Negative Downard unit normal vector}}$$ as shown in Figure 15.6.8. If the smooth orientable surface \(S\) is given in parametric form by \( \textbf{r}(u,v) = x(u,v)\textbf{i} +y(u,v)\textbf{j} + z(u,v)\textbf{k} \:\:\:\: \color{red}{ \text{Parametric surface}}\) then the unit normal vectors are given by $$ \textbf{N} = \frac{\textbf{r}_{u} \times \textbf{r}_{v} }{ \| \textbf{r}_{u} \times \textbf{r}_{v} \| } \:\:\:\: \color{red}{ \text{Upward unit normal vector}}$$ and $$ \textbf{N} = \frac{\textbf{r}_{v} \times \textbf{r}_{u} }{ \| \textbf{r}_{v} \times \textbf{r}_{u} \| } \:\:\:\: \color{red}{ \text{Downward unit normal vector}}.$$ Note that reversing the order for \(\textbf{r}_{u}\) and \(\textbf{r}_{v}\) changes the orientation. For an orientable surface given by \(y=g(x,z) \) or \(x=g(y,z)\) use the gradient vector \(\nabla G(x,y,z)= -g_{x}(x,z)\textbf{i} +\textbf{j} -g_{z}(x,z) \textbf{k} \:\:\:\: \color{red}{\nabla G(x,y,z)=y -g(x,z) } \) or \(\nabla G(x,y,z)= \textbf{i} -g_{y}(y,z)\textbf{j} -g_{z}(y,z) \textbf{k} \:\:\:\: \color{red}{\nabla G(x,y,z)=y -g(y,z) } \) to orient the surface.

Flux Integrals

The velocity field \(\textbf{F}\) indicates the fluid flow direction. Figure 15.6.9

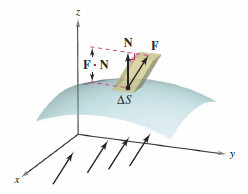
An application for a surface integral in vector form is how a fluid flows through a surface. Consider an oriented surface \(S\) submerged in a fluid having a continuous velocity field \(\textbf{F}\). Let \(\Delta S \) be the area for a small patch on \(S\) over which \(\textbf{F}\) is nearly constant. Then the fluid volume crossing this region per time unit is approximated by the volume for the column with height \(\textbf{F} \cdot \textbf{N}\), as shown in Figure 15.6.9. As an equation, \( \Delta V \) \(= \)(height)(base area) \(= (\textbf{F} \cdot \textbf{N})\: \Delta S.\) Therefore the fluid volume crossing the surface \(S\) per time unit, called the flux of \(\textbf{F}\) across \(S\) is given by the surface integral in Definition 15.6.1.

Definition 15.6.1 Flux Integral

Let \(\textbf{F}(x,y,z) = M\textbf{i} +N \textbf{j} +P \textbf{k}\), where \(M\), \(N\), and \(P\) have continuous first partial derivatives on the surface \(S\) oriented by a unit normal vector \(\textbf{N}\). The flux of \(\textbf{F}\) across \(S\) is given by

$$ \int_{S} \int \textbf{F} \cdot \textbf{N} \: dS.$$

Geometrically, a flux integral is the surface integral over \(S\) for the normal component for \(\textbf{F}\). If \(\rho(x,y,z)\) is the fluid density at \((x,y,z)\), then the flux integral

$$ \int_{S} \int \textbf{F} \cdot \textbf{N} \: dS$$

represents the mass for the fluid flowing across \(S\) per time unit.

To evaluate a flux integral for a surface given by \(z=g(x,y)\), let

\(G(x,y,z) = z-g(x,y)\).

Then, \(\textbf{N} \: dS\) can be written as follows.

\(\textbf{N} \: dS\)	$$=\frac{\nabla G(x,y,z)}{\| \nabla G(x,y,z) \|} \:d S $$
	$$= \frac{\nabla G(x,y,z)}{\sqrt{(g_{x})^{2}+(g_{y})^{2} +1}} \sqrt{(g_{x})^{2}+(g_{y})^{2} +1} \: dA $$
	\(= \nabla G(x,y,z) \: dA \)

For an oriented surface \(S\) given by the vector-valued function

\(\textbf{r}(u,v) = x(u,v)\textbf{i} +y(u,v) \textbf{j} +z(u,v)\textbf{k} \:\:\:\: \color{red}{ \text{Parametric surface }} \)

defined over a region \(D\) in the \(uv\)-plane the flux integral for \(\textbf{F}\) across \(S\) as

$$\int_{S} \int \textbf{F} \cdot \textbf{N} \: dS$$	$$= \int_{D} \int \textbf{F} \cdot \left( \frac{\textbf{r}_{u} \times \textbf{r}_{v}}{\| \textbf{r}_{u} \times \textbf{r}_{v} \|} \right) \|\textbf{r}_{u} \times \textbf{r}_{v} \| \: dS $$
	$$= \int_{D} \int \textbf{F} \cdot (\textbf{r}_{u} \times \textbf{r}_{v}) \: dA$$

Note the similarity between this integral and the line integral

$$ \int_{C} \textbf{F} \cdot \: d\textbf{r} = \int_{C} \textbf{F} \cdot \textbf{T} \: ds$$

A summary for the line and surface integrals discussed so far are presented in Summary 15.6.1.

Theorem 15.6.2 Evaluating a Flux Integral

Let \(S\) be an oriented surface given by \(z=g(x,y)\) and let \(R\) be its projection onto the \(xy\)-plane.

$$ \int_{S} \int \textbf{F} \cdot \textbf{N} \: dS = \int_{R} \int \textbf{N} \cdot [-g_{x}(x,y) \textbf{i} -g_{y}(x,y) \textbf{j} + \textbf{k} ] \: dA \:\:\:\: \color{red}{ \text{Oriented upward }}$$

$$ \int_{S} \int \textbf{F} \cdot \textbf{N} \: dS = \int_{R} \int \textbf{N} \cdot [g_{x}(x,y) \textbf{i} +g_{y}(x,y) \textbf{j} - \textbf{k} ] \: dA \:\:\:\: \color{red}{ \text{Oriented downward }}$$

For the first integral, the surface is oriented upward, and for the second integral, the surface is oriented downward.

Example 15.6.5 Using a Flux Integral to Find the Mass Flow Rate

Figure 15.6.10

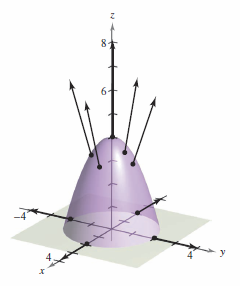
Let \(S\) be the a patch on the paraboloid \(z = g(x,y) = 4-x^{2}-y^{2}\) lying above the \(xy\)-plane, oriented by an upward unit normal vector, as shown in Figure 15.6.10. A fluid with consistent density \(\rho\) is flowing through the surface \(S\) according to the vector field \(\textbf{F}(x,y,z) = x\textbf{i} + y \textbf{j} + z \textbf{k} \). Find the mass flow rate through \(S\). Solution Begin by computing the partial derivatives for \(g\), \(g_{x}(x,y)=-2x\) and \(g_{y}(x,y)=-2y\). The mass flow rate through the surface \(S\) is $$\int_{S} \int \rho \textbf{F} \cdot \textbf{N} \: dS $$ $$= \rho \int_{R} \int \textbf{F} \cdot [ -g_{x}(x,y)\textbf{i} -g_{x}(x,y) \textbf{j} + \textbf{k} ] \: dA$$ $$= \rho \int_{R} \int [ x\textbf{i} + y \textbf{j} + (4-x^{2}-y^{2})\textbf{k} ] \cdot (2x\textbf{i} +2y \textbf{j} + \textbf{k} ) \: dA $$ $$= \rho \int_{R} \int [ 2x^{2} + 2y^{2} + (4-x^{2}-y^{2})] \: dA $$ $$= \rho \int_{R} \int (4+x^{2}+y^{2}) \: dA $$ $$= \rho \int_{0}^{2\pi} \int_{0}^{2} (4+r^{2})r \: dr \:d \theta \:\:\:\: \color{red}{ \text{Polar coordinates }}$$ $$= \rho \int_{0}^{2\pi} 12 \: d\theta = 24 \pi \rho. $$

Example 15.6.6 Finding the Flux for an Inverse Square Field

Figure 15.6.11

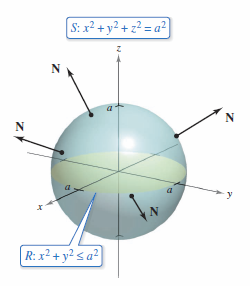
Find the flux over the sphere \(S\) given by \(x^{2}+y^{2}+z^{2} = a^{2} \:\:\:\: \color{red}{ \text{Sphere } S} \) where \( \textbf{F}\) is an inverse square field given by $$ \textbf{F} (x,y,z) = \frac{kq}{\| \textbf{r}\|^{2}} \frac{\textbf{r}}{\| \textbf{r}\|} = \frac{kq\textbf{r}}{\| \textbf{r}\|^{3}} \:\:\:\: \color{red}{ \text{Inverse square field }\textbf{F}} $$ and \(\textbf{r}= x\textbf{i} +y \textbf{j} + z \textbf{k}\). Assume \(S\) is oriented outward, as shown in Figure 15.6.11. Solution The sphere is given by \( \textbf{r}(u,v)\) \(= x(u,v)\textbf{i} +y(u,v) \textbf{j} +z(u,v) \textbf{k}\) \(=a \sin u \cos v \textbf{i} + a \sin u \sin v \textbf{j} + a \cos u \textbf{k}\) where \(0 \leqslant u \leqslant \pi\) and \(0 \leqslant v \leqslant 2 \pi\). The partial derivatives for \(\textbf{r}\) are \( \textbf{r}_{u}(u,v) = a \cos u \cos v \textbf{i} + a \cos u \sin v \textbf{j} - a \sin u \textbf{k} \) and \( \textbf{r}_{v}(u,v) = -a \sin u \sin v \textbf{i} + a \sin u \cos v \textbf{j} \) which implies the normal vector \(\textbf{r}_{u} \times \textbf{r}_{v}\) is $$ \textbf{r}_{u} \times \textbf{r}_{v}$$ $$= \begin{vmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\ a \cos u \cos v & a \cos u \sin v & -a \sin u\\ -a \sin u \sin v & a \sin u \cos v & 0 \end{vmatrix}$$ $$=a^{2}(\sin^{2} u \cos v \textbf{i} + \sin^{2} u \sin v \textbf{j} + \sin u \cos v \textbf{k}). $$ Back substitution produces \( \textbf{F}(x,y,z)\) $$=\frac{kq\textbf{r}}{\| \textbf{r}\|^{3}} $$ $$=kq \frac{x\textbf{i} + y\textbf{j} + z\textbf{k}}{\| x\textbf{i} + y\textbf{j} + z\textbf{k} \|^{3}} $$ $$= \frac{kq}{a^{3}} (a \sin u \cos v \textbf{i} + a\sin u \sin v \textbf{j} + a \cos u \textbf{k}).$$ Multiply the flux integral by the partial derivative product produces \( \textbf{F} \cdot (\textbf{r}_{u} \times \textbf{r}_{v}) \) $$= \frac{kq}{a^{3}} [(a \sin u \cos v \textbf{i} + a\sin u \sin v \textbf{j} + a \cos u \textbf{k}) \cdot \\ \: \: \: \: a^{2}(\sin^{2} u \cos v \textbf{i} + \sin^{2} u \sin v \textbf{j} + \sin u \cos v \textbf{k})]$$ \(= kq(\sin^{3} u \cos^{2} v + \sin^{3} u \sin^{2} v + \sin u \cos^{2} u ) \) \(=kq \sin u. \) Applying Theorem 15.6.2 produces the flux over the sphere \(S\) $$ \int_{S} \int \textbf{F} \cdot \textbf{N} \: dS $$ $$= \int_{D} \int (kq \sin u) \:d A$$ $$= \int_{0}^{2 \pi} \int_{0}^{\pi} kq \sin u \: du \: dv $$ $$= 4 \pi kq. $$

Example 15.6.6 shows that the flux across a sphere \(S\) in an inverse square field is independent from \(S\)'s radius. Note that if \(\textbf{E}\) is an electric field, then the result, along with Coulomb's Law[2], yields Gauss's Law[3] from electrostatics:

$$ \int_{S} \int \textbf{E} \cdot \textbf{N} \: dS = 4 \pi k q \:\:\:\: \color{red}{ \text{Gauss's Law}}$$

where \(q\) is a point charge located at the sphere's center and \(k\) is the Coulomb Constant. Gauss's Law is valid for more general closed surfaces that enclose the origin, and relates the flux from the surface to the total charge \(q\) inside the surface.

Surface integrals are also used to study heat flow. Heat flows from higher temperature area to lower temperature areas in the direction where change is greatest. Therefore, a temperature gradient is used to measure heat flux. The flux depends on the surface area. Heat flowing along the normal direction, normal vector, losses heat, whereas heat flowing in directions tangential to the surface lose no heat. For example, assume the heat flux across surface area portion \(\Delta S \)is given by \(\Delta H \approx -k \nabla T \cdot \textbf{N} \: dS\), where \(T\) is the temperature. The variable \(\textbf{N} \) is the unit normal vector to the surface in the heat flow's direction, and \(k\) is the material's thermal diffusivity. The heat flux across the surface is given by the equation

$$H= \int_{S} \int -k \nabla T \cdot \textbf{N} \: dS.$$

Summary 15.6.1 Line and Surface Integrals

Line Integrals

\( ds \)	\(= \| \textbf{r}^{ \prime }(t) \| \: dt \)
	\(=\sqrt{[x^{\prime}(t)]^{2}+[y^{\prime}(t)]^{2}+[z^{\prime}(t)]^{2}} \:dt \)

$$\int_{C} f(x,y,z) \:ds = \int_{a}^{b} f(x(t),y(t),z(t)) \: ds \:\:\:\: \color{red}{ \text{Scalar form}}$$

$$\int_{C} \textbf{F} \cdot \:d\textbf{r}$$	$$=\int_{C} \textbf{F} \cdot \textbf{T} \:ds $$
	$$=\int_{a}^{b} \textbf{F}(x(t),y(t),z(t)) \cdot \textbf{r}^{\prime}(t) \: dt \:\:\:\: \color{red}{ \text{Vector form}}$$

Surface Integrals \([z=g(x,y)]

\( dS= \sqrt{1+[g_{x}(x,y)]^{2} +[g_{y}(x,y)]^{2}} \: d A\)

$$\int_{S} \int f(x,y,z) \:dS = \int_{S} \int f(x,y,g(x,y))\sqrt{1+[g_{x}(x,y)]^{2} +[g_{y}(x,y)]^{2}} \: dA \:\:\:\: \color{red}{ \text{Scalar form}}$$

$$ \int_{S} \int \textbf{F} \cdot \textbf{N} \: dS = \int_{R} \int \textbf{F} \cdot [-g_{x}(x,y)\textbf{i} -g_{y}(x,y) \textbf{j} + \textbf{k}] \: dA \:\:\:\: \color{red}{ \text{Vector form (upward normal)}}$$

Surface Integrals (parametric form)

\( dS= \| \textbf{r}_{u}(u,v) \times \textbf{r}_{v}(u,v) \| \: d A\)

$$\int_{S} \int f(x,y,z) \:dS = \int_{D} \int f(x(u,v),y(u,v),z(u,v)) \: dS \:\:\:\: \color{red}{ \text{Scalar form}}$$

$$ \int_{S} \int \textbf{F} \cdot \textbf{N} \: dS = \int_{D} \int \textbf{F} \cdot (\textbf{r}_{u} \times \textbf{r}_{v}) \: dA \:\:\:\: \color{red}{ \text{Vector form}}$$

Internal Links

Parent Article: Calculus III 15 Vector Analysis