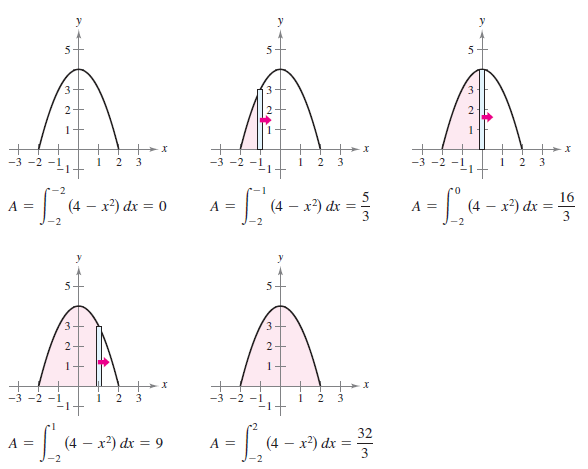Calculus II 07.01 The Area Between Two Curves

Previous	Calculus II 06 Differential Equations
Next	Calculus II 07.02 Volume The Disk Method

7.1 The Area Between Two Curves

• Find the area between two curves using integration.
• Find the area between intersecting curves using integration.
• Describe integration as an accumulation process.

Area Between Two Curves

Figure 7.1.1 Figure 7.1.3

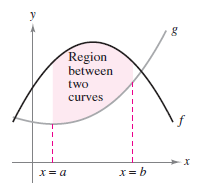
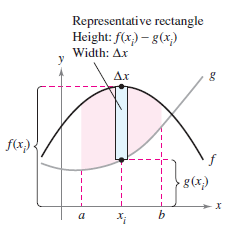
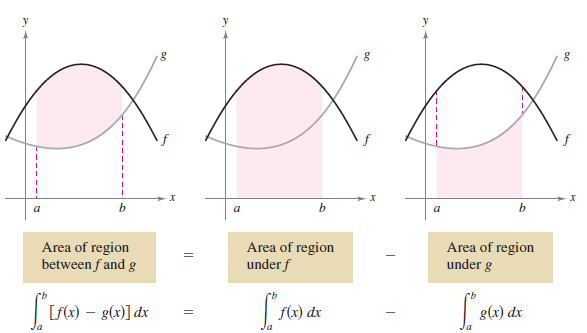
Definite integrals can be extended from the area under a curve to the area between two curves. Consider two functions \(f\) and \(g\) that are continuous on the interval \([a,b]\). The graphs for both \(f\) and \(g\) lie above the \(x\)-axis, and the graph for \(g\) lies below the graph for \(f\) as shown in Figure 7.1.1. The pink area under \(g\)'s graph subtracted from the area under \(f\)'s graph as shown in Figure 7.1.2. Figure 7.1.2 To verify the result shown in Figure 7.1.2, partition the interval \([a,b]\) into subintervals, each with width \(\Delta x\). Then, as shown in Figure 7.1.3, sketch a representative rectangle with width \(\Delta x\) and height \(f(x_{i})-g(x)\) where \(x_{i}\) is in the \(i\)th subinterval. This representative rectangle has the area $$\Delta A_{i}=(height)(width)= \left[ f(x_{i})-g(x_{i}) \right ]\Delta x $$ By adding the areas from \(n\) rectangles and taking the limit as \(\left \| \Delta \right \|\rightarrow 0 \:(n \to \infty)\) yields $$ \lim_{n \to \infty } \sum^{n}_{i=1}[ f(x_{i})-g(x_{i}) ] \Delta x $$ Because \(f\) and \(g\) are continuous on \([ a,b ]\), \(f-g\) is also continuous on \([ a,b ]\) and the limit exists. The region's area is Area $$ = \lim_{n \to \infty } \sum^{n}_{i=1} \left [ f(x_{i})-g(x_{i}) \right ] \Delta x $$ $$=\int^{a}_{b} \left [ f(x)-g(x) \right ]\:dx $$

Theorem 7.1.1 The Area Between Two Curves

If \(f\) and \(g\) are continuous on \([ a,b ]\) and \(g(x) \leqslant f(x)\) for all \(x\) in \([ a,b ]\), then the area bounded by the graphs for \(f\) and \(g\) and the vertical lines \(x=a\) and \(x=b\) is

$$A=\int^{a}_{b} \left [ f(x)-g(x) \right ]\:dx $$

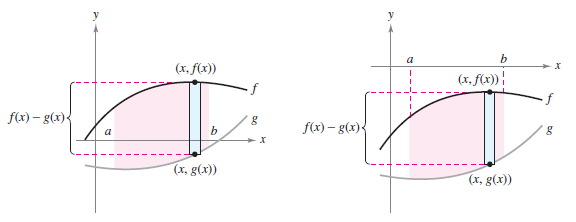
The graphs for \(f\) and \(g\) in Figure 7.1.1 are shown above the \(x\)-axis. This, however, is not necessary. The same integrand \([ f(x)-g(x) ]\) can be used as long as \(f\) and \(g\) are continuous and \(g(x) \leqslant f(x)\) for all \(x\) in the interval \([ a,b ]\). This is summarized graphically in Figure 7.1.4. Notice in Figure 7.1.4 that the height for any representative rectangle is \(f(x)-g(x)\) anywhere on the \(x\)-axis.

Figure 7.1.4

Representative rectangles are used throughout this chapter in various integration applications. A vertical rectangle (with width \(\Delta x\)) implies integration with respect to \(x\), whereas a horizontal rectangle (with width \(\Delta y)\) implies integration with respect to \(y\).

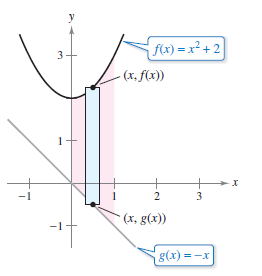
Example 7.1.1 Finding the Area Between Two Curves

The region bounded the graphs for \(f\), \(g\), \(x=0\), and \(x=1\). Figure 7.1.5

Find the area bounded by the graphs \(y=x^{2}+2\), \(y=-x\), \(x=0\), and \(x=1\). Solution Let \(g)=-x\) and \(f(x)=x^{2}+2\). Then \(g(x) \leq f(x)\) for all \(x\) in \([ 0,1 ]\), as shown in Figure 7.1.5. The area for any representative rectangle is \(\Delta A\) \(=[ f(x)-g(x) ]\Delta x\) \(=[(x^{2}+2)-(-x) ]\Delta x\) and the area of the region is: \(A\) $$=\int^{a}_{b}[ f(x)-g(x) ]\:dx $$ $$ = \int^{1}_{0} \left [ (x^{2}+2)-(-x) \right ]\:dx $$ $$ = \left [ \frac {x^{3}}{3}+\frac {x^{2}}{2}+2x \right ]^{1}_{0} $$ $$= \frac {1}{3}+ \frac {1}{2} + 2 = \frac {17}{6}$$

Area for a Region Between Intersecting Curves

In Example 7.1.1, the graphs for \(f(x)=x^{2}+2\) and \(g(x)=-x\) do not intersect, and the values for \(a\) and \(b\) are given explicitly. A more common problem involves a region bounded by two intersecting graphs, where \(a\) and \(b\) must be calculated.

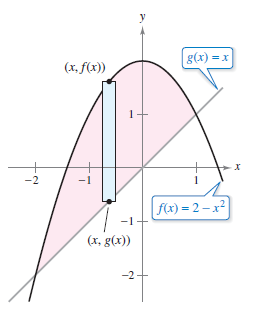
Example 7.1.2 A Region Lying Between Two Intersecting Graphs

The region bounded the graphs for \(f\) and \(g\). Figure 7.1.6

Find the area of the region bounded by the graphs \(f(x)=2-x^{2}\) and \(g(x)=x\). Solution In Figure 7.1.6, notice that the graphs for \(f(x)\) and \(g(x)\) intersect at two points. To find the \(x\)-coordinates, set \(f(x)=g(x)\)and solve for \(x\). \(2-x^{2}=x\) Set \(f(x)\) equal to \(g(x)\) \(-x^{2}-x+2=0 \:\:\:\: \) Write in general form \(-(x+2)(x-1)=0 \:\:\:\: \) Factor \(x=-2 \: or \: 1\) Solve for \(x\). There is always one answer per intersection. \(a=-2 \: and \: b=1\) The values are assigned left to right. Because \(g(x) \leqslant f(x)\) for all \(x\) in the interval \([ -2,1 ]\), the formula for the rectangle area is $$ \Delta A=[ f(x)-g(x) ]\Delta x=[ (2-x^{2})-x ]\Delta x $$ the area is: $$A $$ $$=\int^{1}_{-2} \left [ (2-x^{2})-x \right ] \Delta x $$ $$ = \left [ -\frac{x^{3}}{3}-\frac{x^{2}}{2}+2x \right ]^{1}_{-2} =\frac{9}{2}$$

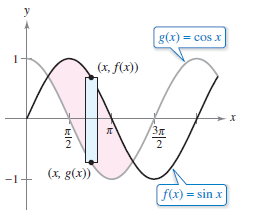
Example 7.1.3 A Region Lying Between Two Overlapping Wave Graphs

One region bounded by the sine and cosine graphs. Figure 7.1.7

Figure 7.1.7 shows sine and cosine curves intersecting infinitely many times, bounding regions with equal areas. Find the area for one region. Solution Let \(g(x)=\cos x\) and \(f(x)=\sin x\). Then \(g(x)\leqslant f(x)\) for all \(x\) in the interval corresponding to the shaded region in Figure 7.1.7. To find the two intersecting points set \(f(x)\) and \(g(x)\) equal to each other and solve for \(x\). \(\sin x\) \( = \cos x\) Set \(f(x)\) equal to \(g(x)\). $$ \frac {\sin x}{\cos x} $$ $$ = 1 $$ Divide each side by \(\cos x\). \(\tan x \) \(= 1\) Trigonometric identity \(x\) $$=\frac {\pi}{4} \text{ or } \frac {5\pi}{4} \text{, } 0 \leqslant x \leqslant 2\pi $$ Solve for \(x\) Assign \(a=\frac {\pi}{4}\) and \(b=\frac {5\pi}{4}\). Because \(\sin x \geqslant \cos x\) for all \(x\) in the interval \([ \frac{\pi}{4}, \frac{5\pi}{4} ]\), the region's area is \(A\) $$=\int^{5\pi/4}_{\pi/4} \left [ \sin x - \cos x \right ]\:dx $$ $$ \LARGE = \left [ -\cos x -\sin x \right]^{5\pi/4}_{\pi/4} =2\sqrt{2}$$

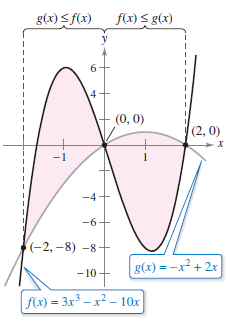
Example 7.1.4 Curves That Intersect At More Than Two Points

On \([-2,0]\), \(g(x) \leqslant f(x)\), and on \([0,2]\), \(f(x)\leqslant g(x)\). Figure 7.1.8

Some curves intersect at more that two points. Some curves intersect for infinite points. Find the area between the following graphs. \(f(x)=3x^{3}-x^{2}-10x\) and \(g(x)=-x^{2}+2x\) Solution Begin by setting \(f(x)\) and \(g(x)\) equal to each other and solving for \(x\). This yields the \(x\)-values at all intersection points between the graphs. \(3x^{3}-x^{2}-10x =-x^{2}+2x \:\:\:\: \) Set \(f(x)\) equal to \(g(x)\) \(3x^{3}-12x=0\) Set equal to zero \(3x(x-2)(x+2)=0\) Factor \(x=-2,0,2\) Solve for \(x\) The graphs intersect when \(x=-2,0,\:\text{and}\:2\). In Figure 7.1.8, notice that \(g(x) \leqslant f(x)\) on the interval \([ -2,0 ]\). The graphs switch at the origin with \(g(x) \geqslant f(x)\) on the interval \([ 0,2 ]\) as \(f\)'s graph moves below \(x=0\). Calculating the total area over the interval \([ -2,2 ]\) requires two integrals, one for each sub-interval. \(A\) $$=\int_{-2}^{0} \left [ f(x)-g(x) \right ]dx+\int_{0}^{2} \left[ g(x)-f(x) \right ]dx$$ $$=\int_{-2}^{0} \left (3x^{3}-12x \right )dx+\int_{0}^{2} \left (-3x^{3}+12x \right)dx$$ $$= \left [ \frac{3x^{4}}{4}-6x^{2} \right ]_{-2}^{0}+ \left [ \frac{-3x^{4}}{4}+6x^{2} \right ]_{0}^{2}$$ \(=-(12-24)+(-12+24) = 24\) Integrating across the interval \( [ -2,2 ]\) will produce an incorrect result, zero, because, in this case, both sub-regions have equal area.

When a region has a graph for a boundary, it is often convenient to use representative rectangles that are horizontal and find the area by integrating with respect to \(y\). In general, determining the area between two curves uses two equations

$$ A $$	$$ = \int^{x_{2}}_{x_{1}}{ \color{red}{ \underbrace{ \color{black}{ \left [ (\text{top curve})-(\text{bottom curve}) \right ]}}_{\text{in variable} \: x}}} dx \:\:\:\: $$	Vertical Rectangles
or
$$ A$$	$$ = \int^{y_{2}}_{y_{1}}{ \color{red}{ \underbrace{ \color{black}{ [ (\text{top curve})-(\text{bottom curve}) ]}}_{\text{in variable} \: y}}} dy $$	Horizontal Rectangles

where \((x_{1},y_{1})\) and \((x_{2},y_{2})\) are either adjacent intersection points on the graphs or points on the specified boundary lines.

Example 7.1.5 Horizontal Representative Rectangles

Horizontal rectangles (integration with respect to \(y\)) Figure 7.1.9 Vertical rectangles (integration with respect to \(x\)) Figure 7.1.10

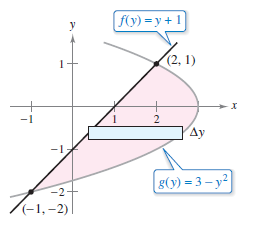
Find the area for the region bounded by the graphs \(x=3-y^{2}\) and \(x=y+1\). Solution Rewrite the equations as \(g(y)=3-y^{2}\) and \(f(y)=y+1\) Rewrite in \(y\) terms allows for a solution in \(y\) terms. These two curves intersect when \(y=-2\) and \(y=1\), as shown in Figure 7.1.9. Because \(f(y) \leqslant g(y)\) on this interval integration will produce the area \(\Delta A = [ g(y)-f(y) ]\Delta y=[ (3-y^{2})-(y+1) ]\:\Delta y\) This makes the area $$A$$ $$ = \int^{1}_{-2} \left [ (3-y^{2})-(y+1) \right ] \:dy $$ $$ = \int^{1}_{-2} (-y^{2}-y+2)\: dy $$ $$ = \left [ \frac{-y^{2}}{3}-\frac{y^{2}}{2}+2y \right ]^{1}_{-2} $$ $$ = \left (-\frac{1}{3}-\frac{1}{2}+2 \right )- \left (\frac{8}{3}-2-4 \right ) =\frac{9}{2}$$ 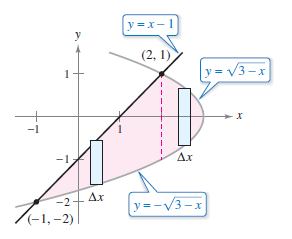Notice that by integrating with respect to \(y\), only one integral is needed. To integrate with respect to \(x\) requires two integrals because the upper boundary changes at \(x=2\), as shown in Figure 7.1.10. $$A$$ $$=\int_{-1}^{2} \left [ (x-1)+\sqrt{3-x} \right ]\:dx\:+\int_{2}^{3} \left ( \sqrt{3-x}-\sqrt{3-x} \:\right) \:dx $$ $$=\int_{-1}^{2} \left [ x-1+(3-x)^{1/2} \right ]\:dx\:+2\int_{2}^{3}(3-x)^{1/2}\:dx $$ $$= \left[ \frac{x^{2}}{2}-x-\frac{(3-x)^{3/2}}{3/2} \right ]^{2}_{-1}-2 \left[ \frac{(3-x)^{3/2}}{3/2} \right ]^{3}_{2} $$ $$= \left(2-2-\frac{2}{3} \right )- \left(\frac{1}{2}+1-\frac{16}{3} \right )-2(0)+2 \left (\frac{2}{3} \right )=\frac{9}{2}$$

Integration as an Accumulation Process

The integration formula for the area between two curves was developed by using a rectangle as the representative element. From now on an appropriate representative element will be constructed using familiar precalculus formulas. Each integration formula will then be obtained by summing or accumulating these representative elements.

$$ \text{Known Precalculus Formula } \rightarrow \text{ Representative Element }\rightarrow \text{ New Integration Formula }$$

For example, the area formula in this section was developed as follows.

$$ A = (height)(width) \rightarrow \Delta A = \left [ f(x)-g(x) \right ]\Delta x \rightarrow A = \int^{b}_{a} \left [ f(x)-g(x) \right ]\:dx $$

Example 7.1.6 Integration as an Accumulation Process

Similar to Calculus I 03.05 Limits at Infinity in accumulating area under, or between, curves by expanding the interval, as illustrated here. Find the area bounded by the graph for \(y=4-x^{2}\) and the \(x\) axis. Describe the integration as an accumulation process.
Solution The region has the total area

$$ A = \int^{2}_{-2} \left ( 4-x^{2} \right )\:dx $$

Watch the area increase as the representative rectangle slides left to right, from \(x=-2\) to \(x=2\) as shown in Figure 7.1.11. As the rectangle shifts the total area increases from 0, to 5/3, to 16/3, to 9, and finally to 32/2.

Figure 7.1.11

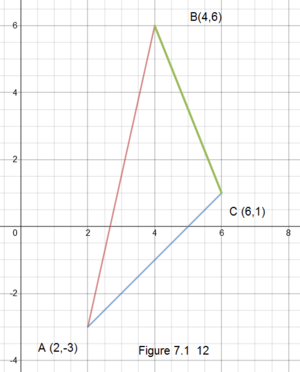
Example 7.1.7 Find a Triangle's Area using Integration and Vertices

Figure 7.1.12

Use integration to find the area for the figure having the given vertices (2,-3),(4,6), and (6,1). Solution Observe the figure is a triangle and find the area using the Three Vertices Formula: Vertex Labels \(A=(2,-3),\:B=(4,6) \text{, and } C=(6,1)\) \(Area\) $$= \left[ \frac{A_{x}(B_{y}-C_{y})+B_{x}(C_{y}-A_{y})+C_{x}(A_{y}-B_{y})}{2} \right ] $$ $$= \left [ \frac{2(6-1)+4(1-(-3))+6(-3-6)}{2} \right ]=14 $$ To use integration, find the equation for each side and integrate along the \(x\) variable. Finally, sum the absolute values. From precalculus, all lines have the form \(y=mx+b\) where $$(x_{1},y_{1}),(x_{2},y_{2})\text{, are points on the line, the slope is }m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \text{ and }b \text{ is the }y \text{ offset.}$$ For side \(AB\): \(m\) $$=\frac{6-(-3)}{4-2} = \frac{9}{2} $$ for the points (2,-3) and (4,6) \(-3\) $$ = \frac{9}{2}2+b$$ Plug in Vertex \(A\) to get \(b\) \(-12\) \(=b \) \(y\) $$=\frac{9}{2}x-12$$ The equation for \(AB\) \(AB \: Area\) $$=\int_{2}^{4}\frac{9}{2}x-12\:dx $$ Integrate with respect to \(x\) and take the absolute value to get the area. $$= \left [9x^{2}-12x+C \right ]_{2}^{4}=3 $$ \(AC\:Area \) \(=|-4|=4\) \(BC\:Area \) \(=7\) Summing all three produces \(3+4+7=14\) which matches the verified answer.

Internal Links

Parent Article: Calculus II 07 Integration Applications