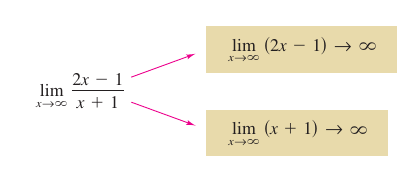Calculus I 03.05 Limits at Infinity

Previous	Calculus I 03.04 Concavity and the Second Derivative Test
Next	Calculus I 03.06 Curve Sketching

3.5 Limits at Infinity

• Determine finite limits at infinity.
• Determine the horizontal asymptotes, if any, for a function's graph.
• Determine infinite limits at infinity.
• Limits at Infinity

Limits at Infinity

The limit for \(f(x)\) as \(x\) approaches \(-\infty\) or \(\infty\) is 3. Figure 3.5.1

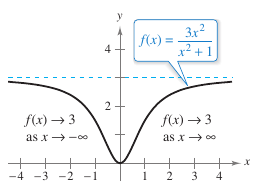
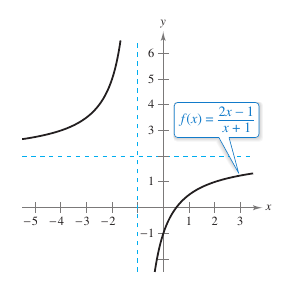
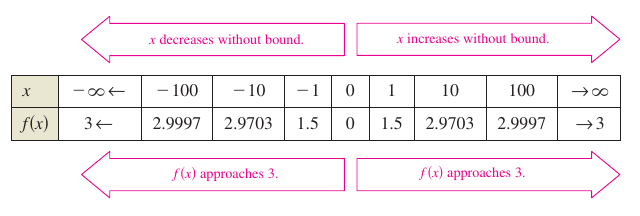
Functions display "end behavior" on an infinite interval. Consider the graph for $$f(x)=\frac{3x^2}{x^2+1}$$ as shown in Figure 3.5.1. As the graph for \(f(x)\) approaches 3 as \(x\)-values increase or decrease without bound. Table 3.5.1 displays the same conclusions numerically. Table 3.5.1 Table 3.5.1 suggests that the value for \(f(x)\) approaches 3 as \(x\) increases without bound \((x \to \infty)\). Conversely, \(f(x)\) approaches 3 as \(x\) decreases without bound \((x \to -\infty)\). 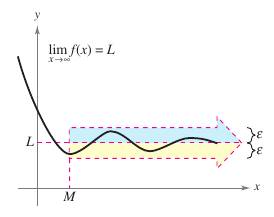Limits at infinity are denoted by \(\lim_{x \to -\infty} f(x)=3\)     Limit at negative infinity and \(\lim_{x \to \infty} f(x)=3\)     Limit at positive infinity The statement \(\lim_{x \to - \infty} f(x)=L\) or \(\lim_{x \to \infty} f(x)=L\) means the limit exists and the limit is equal to \(L\). To say that a statement is true as \(x\) increases without bound means that for some really large real number \(M\), the statement is true for all \(x\) in the interval \(\left \{x:\:x >M \right \} \). Definition 3.5.1 formally states this concept.

Definition 3.5.1 Limits at Infinity

\(f(x)\) is within \(\varepsilon\) units from \(L\) as \(x \to \infty\). Figure 3.5.2

Let \(L\) be a real number. 1. The statement \(\lim_{x \to \infty} f(x)=L\) means that for each \(\varepsilon >0\) there exists an \(M>0\) such that \(\left | f(x)-L \right | < \varepsilon \) whenever \(x>M\). 2. The statement \(\lim_{x \to -\infty} f(x)=L\) means that for each \(\varepsilon >0\) there exists an \(N<0\) such that \(\left | f(x)-L \right | < \varepsilon \) whenever \(x<N\). Definition 3.5.1 is shown in Figure 3.5.2. Note that for a given positive number \(\varepsilon\), there exists a positive number \(M\) such that, for \(x>M\), the graph for \(f\) will lie between the horizontal lines \(y=L+\varepsilon\) and \(y=L-\varepsilon\).

Horizontal Asymptotes

Figure 3.5.2 displays the graph for \(f\) as it approaches the line \(y=L\) as \(x\) increases without bound. The line \(y=L\) is called a horizontal asymptote for \(f\)'s graph.

Definition 3.5.2 Horizontal Asymptotes

The line \(y=L\) is a horizontal asymptote for \(f\)'s graph when

\(\lim_{x \to -\infty} f(x)= L \text{ or } \lim_{x \to \infty} f(x)= L .\)

It follows that any function's graph can have at most two horizontal asymptotes, one to the left and one to the right.

Limits at Infinity share properties with limits as discussed in Section 1.3. For example, if \(\lim_{x \to \infty} f(x)\) and \(\lim_{x \to \infty} g(x)\) both exist, then

$$\lim_{x \to \infty} \left [ f(x) + g(x) \right ] = \lim_{x \to \infty} f(x) + \lim_{x \to \infty}g(x)$$

and

$$\lim_{x \to \infty} \left [ f(x)g(x) \right ] = \left [ \lim_{x \to \infty} f(x)\right] \left[\lim_{x \to \infty}g(x) \right ].$$

Similar properties hold for limits at \(-\infty\).

Theorem 3.5.1 Limits at Infinity

If \(r\) is a positive rational number and \(c\) is any real number, then

$$\lim_{x \to \infty} \frac{c}{x^r}=0.$$

Furthermore, if \(x^r\) is defined when \(x<0\), then

$$\lim_{x \to -\infty} \frac{c}{x^r}=0.$$

Example 3.5.1 Finding a Horizontal Limit at Infinity

\(y=5\) is a horizontal asymptote. Figure 3.5.3

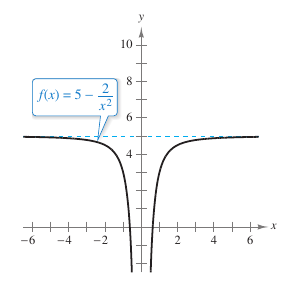
Find the limit: $$\lim_{x \to \infty} \left ( 5-\frac{2}{x^r} \right ).$$ Solution Applying Theorem 3.4.4 produces $$\lim_{x \to \infty} \left ( 5-\frac{2}{x^r} \right )$$ $$=\lim_{x \to \infty} 5 - \lim_{x \to \infty} \frac{2}{x^2}$$     Limits property \(=5-0\) \(=5.\) Therefore, the line \(y=5\) is a horizontal asymptote to the right. By finding the limit $$\lim_{x \to -\infty} \left ( 5-\frac{2}{x^r} \right )$$     Limit as \(x \to - \infty\). yields that \(y=5\) is also a horizontal asymptote from the left, as shown in Figure 3.5.3.

Example 3.5.2 Finding a Horizontal and Vertical Limit at Infinity

\(y=5\) is a horizontal asymptote. Figure 3.5.4

Find the limit: $$\lim_{x \to \infty} \frac{2x-1}{x+1}.$$ Solution Note that the numerator and denominator approach infinity as \(x\) approaches infinity. This results in \(\frac{\infty}{\infty}\), an indeterminate form. To solve it divide the numerator and denominator by the highest power for \(x\) in the denominator. $$\lim_{x \to \infty} \frac{2x-1}{x+1}$$ $$=\lim_{x \to \infty}\frac{ \frac{2x-1}{x}}{\frac{x+1}{x}}$$     Divide numerator and denominator by \(x\). $$=\lim_{x \to \infty} \frac{ 2-\frac{1}{x}}{1+\frac{1}{x}}$$     Simplify. $$=\frac{ \lim_{x \to \infty}2 - \lim_{x \to \infty} \frac{1}{x}}{ \lim_{x \to \infty}1 + \lim_{x \to \infty} \frac{1}{x}}$$     Take the limits for numerator and denominator $$= \frac{2-0}{1+0}$$     Apply Theorem 3.4.4 \(=2\) Therefore, the line \(y=2\) is a horizontal asymptote to the right. By taking the limit as \(x \to -\infty\) produces a horizontal asymptote to the left, as shown in Figure 3.5.4.

Example 3.5.3 Comparing Three Rational Functions

Find each limit.

$$\textbf{a. }\:\lim_{x \to \infty} \frac{2x+5}{3x^2+1} \:\:\:\:\textbf{b. }\:\lim_{x \to \infty} \frac{2x^2+5}{3x^2+1}\textbf{c. }\:\lim_{x \to \infty} \frac{2x^3+5}{3x^2+1}$$

Solution Solving each case produces the indeterminate form \(\infty/\infty\).
a. Divide both numerator and denominator by \(x^2\).

$$\lim_{x \to \infty} \frac{2x+5}{3x^2+1}=\lim_{x \to \infty} \frac{(2/x)+(5/x^2)}{3+(1/x^2)}=\frac{0+0}{3+0}=\frac{0}{3}=0$$

b. Divide both numerator and denominator by \(x^2\).

$$\lim_{x \to \infty} \frac{2x^2+5}{3x^2+1}=\lim_{x \to \infty} \frac{2+(5/x^2)}{3+(1/x^2)}=\frac{2+0}{3+0}=\frac{2}{3}$$

c. Divide both numerator and denominator by \(x^2\).

$$\lim_{x \to \infty} \frac{2x^3+5}{3x^2+1}=\lim_{x \to \infty} \frac{2x+(5/x^2)}{3+(1/x^2)}=\frac{\infty}{3}$$

Therefore, the limit does not exist because the numerator increases without bound while the denominator approaches 3.

Guidelines For Finding Limits \(\pm \infty\) For Rational Functions

1. If the numerator's degree is less than the denominator's degree, then the rational function's limit is 0.
2. If the numerator's degree is equal the denominator's degree, then the rational function's limit is the ratio with the leading coefficients.
3. If the numerator's degree is greater than the denominator's degree, then the rational function's limit does not exist.

\(f\) has a horizontal asymptote at \(y=0\). Figure 3.5.5

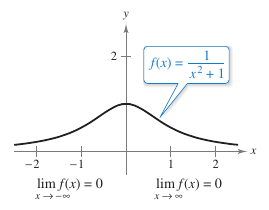
The guidelines for finding limits at infinity for rational functions seem reasonable considering large values for \(x\), the highest-power term for the rational function is the most "influential" in determining the limit. For example, $$\lim_{x \to \infty} \frac{1}{x^2+1}$$ is 0 because the denominator overpowers the numerator as \(x\) increases or decreases without bound, as shown in Figure 3.5.5. The function shown in Figure 3.5.5 is a special case for a curve studied by the Italian mathematician Maria Gaetana Agnesi[1]. The general form is $$f(x)=\frac{8a^3}{x^2+4a^2}.$$     Witches of Agnesi Through a mistranslation of the Italian word vertéré, the curve is known as the Witches of Agnesi. Agnesi's work with this curve first appeared in a comprehensive text on calculus published in 1748.

Figure 3.5.5 shows the function

$$f(x)=\frac{1}{x^2+1}$$

approaching the same horizontal asymptote to the right and left. This is always true for rational functions. Irrational functions may approach different horizontal asymptotes to the right and left. This is demonstrated in Example 3.5.4.

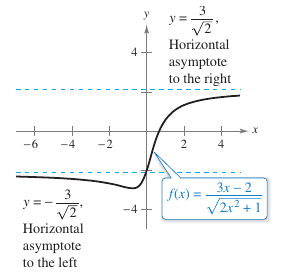
Example 3.5.4 A Function with Two Horizontal Asymptotes

Irrational functions may have different left and right horizontal aymptotes. Figure 3.5.6

Find each limit. $$\textbf{a. }\lim_{x \to \infty} \frac{3x-2}{\sqrt{2x^2+1}}\:\:\:\: \textbf{b. }\lim_{x \to -\infty} \frac{3x-2}{\sqrt{2x^2+1}}$$ Solution a. For \(x>0\) use \(x=\sqrt{x^2}\). Dividing the numerator and denominator by \(x\) produces. $$ \frac{3x-2}{\sqrt{2x^2+1}}= \frac{\frac{3x-2}{x}}{\frac{\sqrt{2x^2+1}}{\sqrt{x^2}}}=\frac{3-\frac{2}{x}}{\sqrt{\frac{2x^2+1}{x^2}}}=\frac{3-\frac{2}{x}}{\sqrt{2+\frac{1}{x^2}}}$$ Taking the limit produces. $$\lim_{x \to \infty}\frac{3x-2}{\sqrt{2x^2+1}}=\lim_{x \to \infty}\frac{3-\frac{2}{x}}{\sqrt{2+\frac{1}{x^2}}}=\frac{3-0}{\sqrt{2+0}} = \frac{2}{\sqrt{2}}$$ b. For \(x<0\) use \(x=\sqrt{x^2}\). Dividing the numerator and denominator by \(x\) produces. $$ \frac{3x-2}{\sqrt{2x^2+1}}=\frac{\frac{3x-2}{x}}{\frac{\sqrt{2x^2+1}}{-\sqrt{x^2}}}=\frac{3-\frac{2}{x}}{-\sqrt{\frac{2x^2+1}{x^2}}}=\frac{3-\frac{2}{x}}{-\sqrt{2+\frac{1}{x^2}}}$$ Taking the limit produces. $$\lim_{x \to -\infty}\frac{3x-2}{\sqrt{2x^2+1}}=\lim_{x \to -\infty}\frac{3-\frac{2}{x}}{-\sqrt{2+\frac{1}{x^2}}}=\frac{3-0}{-\sqrt{2+0}} = -\frac{2}{\sqrt{2}}$$ Figure 3.5.6 displays the graph.

The Squeeze Theorem can evaluate limits at infinity.

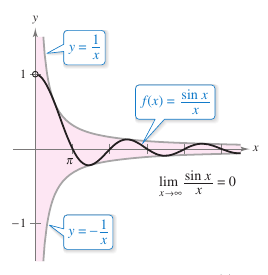
Example 3.5.5 Limits with Trigonometric Functions

As \(x\) increases without bound, \(f(x)\) approaches 0. Figure 3.5.7

Find each limit. $$\textbf{a. }\lim_{x \to \infty} \sin x\:\:\:\: \textbf{b. }\lim_{x \to \infty} \frac{\sin x}{x}$$ Solution a. As \(x\) approaches infinity the sine function oscillates between 1 and -1. This limit does not exist. b. Because \(-1 \leq \sin x \leq 1\), it follow that for \(x>0\). $$-\frac{1}{x} \leq \frac{ \sin x}{x} \leq \frac{1}{x}$$ where $$\lim_{x \to \infty} \left ( -\frac{1}{x} \right )=0\:\:\:\:\textbf{ and }\:\:\:\:\lim_{x \to \infty}\frac{1}{x}=0.$$ Applying the Squeeze Theorem produces $$\lim_{x \to \infty} \frac{ \sin x}{x} = 0$$ as shown in Figure 3.5.7.

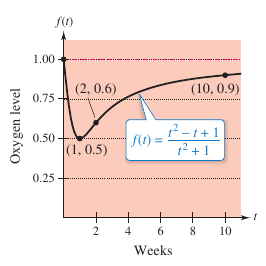
Example 3.5.6 Oxygen Level in a Pond

Oxygen level in a pond approaches the normal level, 1, as \(t\) approaches \(\infty\). Figure 3.5.8

Let \(f(t)\) measure the oxygen level in a pond, where \(f(t)=1\) is the normal, unpolluted level and time \(t\) is measured in weeks. When \(t=0\), organic waste is dumped into the pond. As the waste material oxidizes, the oxygen level is expressed as $$f(t)=\frac{t^2-t+1}{t^2+1}.$$ After 1 week what is the oxygen level as a percentage from normal? After 2 weeks? After 10 weeks? What is the limit as \(t\) approaches infinity? Solution When \(t=1, \:2, \text{ and }10\), the oxygen levels are shown below. $$f(\color{red}{1})=\frac{ \color{red}{1}^2-\color{red}{1}+1}{\color{red}{1}^2+1}=\frac{1}{2}=50\text{%}$$     1 week $$f(\color{red}{2})=\frac{ \color{red}{2}^2-\color{red}{2}+1}{\color{red}{2}^2+1}=\frac{3}{5}=60\text{%}$$     2 week $$f(\color{red}{10})=\frac{ \color{red}{10}^2-\color{red}{10}+1}{\color{red}{10}^2+1}=\frac{91}{101}\approx 90.1\text{%}$$     10 week Find the limit as \(t\) approaches infinity by applying the guidelines or divide the numerator and denominator by \(t^2\) to obtain $$\lim_{t \to \infty} \frac{t^2-t+1}{t^2+1}=\lim_{t \to \infty} \frac{1-(1/t)+(1/t^2)}{1+(1/t^2)}=\frac{1-0+0}{1+0}=1=100\text{%}.$$ as shown in Figure 3.5.8.

Infinite Limits at Infinity

Many functions do not approach a finite limit as \(x\) increases or decreases without bound. For example, no polynomial function has a finite limit at infinity. Definition 3.5.3 describes how polynomial and other functions behave at infinity.

Definition 3.5.3 Infinite Limits at Infinity

Let \(f\) be a differentiable function defined on the interval \((a,\infty)\).
1. The statement \(\lim_{x \to \infty}f(x)=\infty\) means that for each positive number \(M\), there is a corresponding number \(N>0\) such that \(f(x)>M\) whenever \(x>N\).
2. The statement \(\lim_{x \to \infty}f(x)=-\infty\) means that for each negative number \(M\), there is a corresponding number \(N>0\) such that \(f(x)<M\) whenever \(x>N\).
Definition 3.5.3 can be extended to these statements

$$\lim_{x \to -\infty}f(x)=\infty \text{ and }\lim_{x \to -\infty}f(x)=-\infty.$$

Determining if a function has an infinite limit at infinity is useful in analyzing the “end behavior” for its graph. This is described in Section 3.6 Curve Sketching.

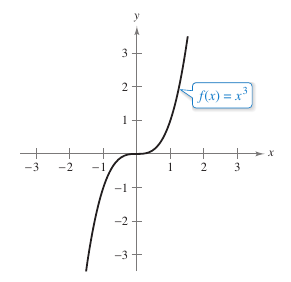
Example 3.5.7 Finding Infinite Limits at Infinity for Polynomial Functions

Figure 3.5.9

Find each limit. $$\textbf{a. } \lim_{x \to \infty} x^3\:\:\:\:\textbf{b. } \lim_{x \to -\infty} x^3$$ Solution a. As \(x\) increases without bound, \(x^3\) also increases without bound. It can be written as $$ \lim_{x \to \infty} x^3=\infty.$$ b. As \(x\) decreases without bound, \(x^3\) also decreases without bound. It can be written as $$ \lim_{x \to -\infty} x^3=-\infty.$$ Figure 3.5.9 shows the graph for \(f(x)=x^3\) these two results.

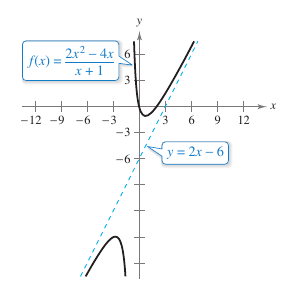
Example 3.5.8 Finding Infinite Limits at Infinity for Fractional-Polynomial Functions

Figure 3.5.10

Find each limit. $$\textbf{a. } \lim_{x \to \infty} \frac{2x^2-4x}{x+1}\:\:\:\:\textbf{b. } \lim_{x \to -\infty} \frac{2x^2-4x}{x+1}$$ Solution a. As \(x\) increases without bound, \(x^3\) also increases without bound. It can be written as $$ \lim_{x \to \infty} \frac{2x^2-4x}{x+1}=\lim_{x \to \infty} \left ( 2x-6+\frac{6}{x+1} \right )= \infty.$$ b. As \(x\) decreases without bound, \(x^3\) also decreases without bound. It can be written as $$ \lim_{x \to -\infty} \frac{2x^2-4x}{x+1}=\lim_{x \to -\infty} \left ( 2x-6+\frac{6}{x+1} \right )=-\infty.$$ As \(x\) approaches \(\pm \infty\), the function \( f(x)=(2x^2-4x)/(x+1) \) behaves like the function \(g(x)=2x-6\). Section 3.6 describes this as line \(y=2x-6\) is a slant asymptote to \(f\)'s graph, as shown in Figure 3.5.10. Figure 3.5.9 shows the graph for \(f(x)=x^3\) these two results.

Internal Links

Parent Article: Calculus I 03 Differentiation Applications