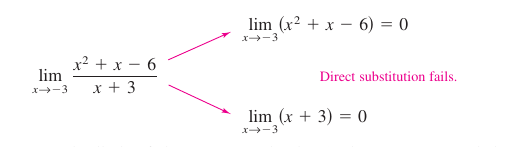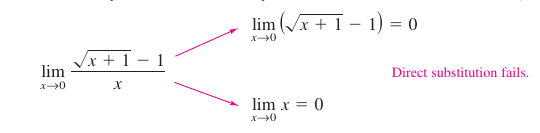Calculus I 01.03 Evaluating Limits Analytically

Previous	Calculus I 01.02 Finding Limits Graphically and Numerically
Next	Calculus I 01.04 Continuity and One-Sided Limits

Evaluating Limits Analytically

• Evaluate a limit using limit properties.
• Develop and use a strategy for finding limits.
• Evaluate a limit using the dividing out technique.
• Evaluate a limit using the rationalizing technique.
• Evaluate a limit using the Squeeze Theorem.

Limit Properties

Area under a curve. Figure 1.3.1

Section 1.2 described that the limit for \(f(x)\) as \(x\) approaches \(c\) does not depend on the value for \(f(x)\) at \(x=c\). Direct substitution can evaluate the limit in this case. That is, $$\lim_{x \to c} f(x)= f({\color{Red}c}).$$     Substitute \(c\) for \(x\). Such well-behaved functions are continuous at \(c\). Section 1.4 will describe this in more detail. Theorem 1.3.1 Three Basic Limits Let \(b\) and \(c\) be real numbers, and let \(n\) be a positive integer. 1. \(\lim_{x \to c} b = b\) 2. \(\lim_{x \to c} x =c\) 3. 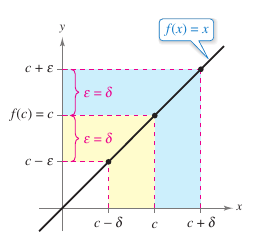\(\lim_{x \to c} x^n = c^n\) Proof To prove Property 2 show that for each \(\epsilon > 0\) there exists a \(\delta > 0\) such that \(\left | x-c \right | < \epsilon\) whenever \(0<\left | x-c \right | < \delta \). The obvious first choice is \(\delta = \epsilon\). The second inequality then implies the first, as shown in Figure 1.3.1. The proofs for Properties 1 and 3 in Theorem 1.3.1 are left for the student.

Theorem 1.3.2 Limit Properties

Let \(b\) and \(c\) be real numbers, and let \(n\) be a positive integer, and let \(f\) and \(g\) be functions with the limits $$\lim_{x \to c} f(x)=L \text { and } \lim_{x \to c} g(x) = K. $$
1. Scalar multiple:	\( \lim_{x \to c} [bf(x)]=bL \)
2. Sum or difference:	\( \lim_{x \to c} [f(x) \pm g(x)]= L \pm K \)
3. Product:	\( \lim_{x \to c} [f(x)g(x)] = LK\)
4. Quotient:	$$ \lim_{x \to c} \frac{f(x)}{g(x)}= \frac{L}{K}, K \neq 0$$
5. Power:	\( \lim_{x \to c} [f(x)]^n = L^n\)

Example 1.3.1 The Polynomial Limit

Find the limit: \(\lim_{x \to 2} (4x^2+3)\).
Solution

$$\lim_{x \to 2} (4x^2+3)$$	$$=\lim_{x \to 2} 4x^2 + \lim_{x \to 2}3$$		Property 2, Theorem 1.3.2
	$$= 4 \left ( \lim_{x \to 2} x^2 \right ) + \lim_{x \to 2}3$$		Property 1, Theorem 1.3.2
	\(= 4(2^2) + 3\)		Properties 1 and 3, Theorem 1.3.1
	\(=19\)		Simplify.

Note in Example 1.3.2 that as the limit (as \(x\) approaches 2) for the polynomial function \(p(x)=4x^2+3\) is simply the value for \(p\) at \(x=2\).

$$\lim_{x \to 2} p(x) = p({\color{Red}2 } )=4({\color{Red}2 }^2)+3=19$$

This direct substitution property is valid for all polynomial and rational functions with nonzero denominators.

Theorem 1.3.3 Polynomial and Rational Function Limits

If \(p\) is a polynomial function ath \(c\) is a real number, then $$\lim_{x \to c} p(x)=p(c).$$

If \(r\) is a rational function given by \(r(x)=p(x)/q(x)\) and \(c\) is a real number such that \(q(c)\neq 0\), then $$\lim_{x \to c} r(x)=r(c)= \frac{p(c)}{q(c)}.$$

Example 1.3.2 The Rational Function Limit

Find the limit:

$$\lim_{x \to 1} \frac{x^2+x+2}{x+1}.$$

Solution Because the denominator is no 0 when \(x=1\),Theorem 1.3.3 can be applied to obtain

$$\lim_{x \to 1} \frac{x^2+x+2}{x+1}=\frac{1^2+1+2}{1+1}=\frac{4}{2}=2.$$

Algebraic functions come in three basic types, polynomial, rational, and radical. Theorem 1.3.4 describes limits with radical functions.

Theorem 1.3.4 Radical Functions with Limits

Let \(n\) be a positive integer. The limit below is valid for all \(c\) when \(n\) is odd, and is valid for all \(c>0\) when \(n\) is even. $$\lim_{x \to c} \sqrt[n]{x}=\sqrt[n]{c}$$

Theorem 1.3.5 Composite Function Limits

If \(f\) and \(g\) are functions such that $$\lim_{x \to c} g(x) = L$$ and $$\lim_{x \to L}f(x) = f(L)$$ then $$\lim_{x \to c} f(g(x))=f \left( \lim_{x \to c} g(x) \right )= f(L).$$

Example 1.3.3 Composite Function Limits

Find the limit.
a.  \(\lim_{x \to 0} \sqrt{x^5+4}\)    b.  \(\lim_{x \to 0} \sqrt[3]{2x^2-10}\)
Solution
a. Because

$$\lim_{x \to 0} (x^2+4)=0^2+4=4 \text{ and }\lim_{x \to 4}\sqrt{x} = \sqrt{4}=2$$

the conclusion is

$$\lim_{x \to 0} \sqrt{x^5+4} = \sqrt{4}=2.$$

b. Because

$$\lim_{x \to 3} (2x^2-10)=2(3^2)-10=8 \text{ and }\lim_{x \to 8}\sqrt[3]{x} = \sqrt[3]{8}=2$$

the conclusion is

$$\lim_{x \to 3} \sqrt[3]{2x^2-10} = \sqrt[3]{8}=2.$$

Many limits for algebraic functions can be evaluated through direct substitution. The six basic trigonometric functions also exhibit this quality, as shown in the Theorem 1.3.6.

Theorem 1.3.6 Trigonometric Functions Limits

Let \(c\) be a real number in the domain for the given trigonometric functions.
1. \( \lim_{x \to c} \sin x = \sin c \)	2. \( \lim_{x \to c} \cos x = \cos c \)	3. \( \lim_{x \to c} \tan x = \tan c \)
4. \( \lim_{x \to c} \cot x = \cot c \)	5. \( \lim_{x \to c} \sec x = \sec c \)	6. \( \lim_{x \to c} \csc x = \csc c \)

Example 1.3.4 Trigonometric Function Limits

$$\text{a. }\lim_{x \to 0} \tan x = \tan(0)=0$$

$$\text{b. }\lim_{x \to \pi} (x \cos x) = \left ( \lim_{x \to \pi} x \right ) \left ( \lim_{x \to \pi} \cos x \right )=\pi \cos (\pi) = - \pi$$

$$\text{c. }\lim_{x \to 0} \sin^2 x = \lim_{x \to 0} (\sin x)^2 = 0^2 = 0$$

A Strategy for Finding Limits

\(f\) and \(g\) agree at all but one point. Figure 1.3.2

Direct substitution and Theorem 1.3.7 together can be used to develop a strategy for finding limits. Theorem 1.3.7 Functions That Agree at All But One Point Let \(c\) be a real numbers, and let \(f(x)=g(x)\) for all \(x \neq c\) in an open interval containing \(c\). 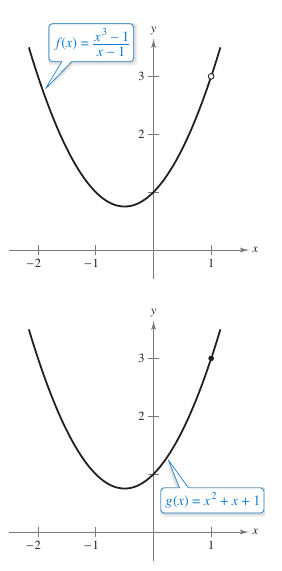If the limit for \(g(x)\) as \(x\) approaches \(c\) exists, then the limit for \(f(x)\) also exists and $$\lim_{x \to c} f(x) = \lim_{x \to c} g(x).$$ Example 1.3.5 Finding the Limit for a Function Find the limit. $$\lim_{x \to 1} \frac{x^3 -1}{x-1}$$ Solution Let \(f(x)=(x^3-1)/(x-1)\). By factoring and dividing out like factors produces $$\require{cancel} f(x)=\frac{\cancel{(x-1)}(x^2+x+1)}{\cancel{(x-1)}}=x^2+x+1=g(x), \text{ } x \neq 1.$$ For all \(x\)-values other than \(x=1\), the functions \(f\) and \(g\) agree, as shown in Figure 1.3.2. Because \(\lim{x \to 1} g(x)\) exists Theorem 1.3.7 can be applied to conclude that \(f\) and \(g\) have the same limit at \(x=1\). $$\lim_{x \to 1} \frac{x^3 -1}{x-1}$$ $$= f(x)=\frac{(x-1)(x^2+x+1)}{(x-1)}$$      Factor. $$=\require{cancel} f(x)=\frac{\cancel{(x-1)}(x^2+x+1)}{\cancel{(x-1)}}$$      Divide out like factors. $$\lim{x \to 1}(x^2+x+1)$$      Apply Theorem 1.3.7 \(=1^2+1+1\)      Use direct substitution \(=3\)      Simplify

A Strategy for Finding Limits

1.Learn to recognized which limits can be evaluated by direct substitution. (These limits are listed in Theorems 1.3.1 to 1.3.6.)

2. When the limit for \(f(x)\) as \(x\) approaches \(c\) cannot be evaluated by direct substitution, try to find a function \(g\) that agrees with \(f\) for all \(x\) other than \(x=c\). [Choose \(g\) such that the limit for \(g(x)\) can be evaluated by direct substitution.] Then apply Theorem 1.3.7 to conclude analytically that $$\lim{x \to c} f(x) = \lim{x \to c} g(x)=g(c).$$

3. Use a graph or table to reinforce your conclusion.

4.This strategy only work when a limit exists.

Dividing Out Technique

\(f\) is undefined when \(x=-3\). Figure 1.3.3

The Dividing Out Technique finds the limit by dividing out common factors. Example 1.3.6 Dividing Out Technique Find the limit: $$\lim_{x \to -3} \frac{x^2+x-6}{x+3}.$$ Solution Though the function is rational Theorem 1.3.3 cannot be applied because the denominator is 0. The limits for the denominator and numerator are 0. Both have a common factor in \((x+3)\). For all \(x \neq -3\) this factor can be divided out to produce $$\require{cancel} f(x)=\frac{x^2+x-6}{x+3}=\frac{\cancel{(x+3)}(x^2+x+1)}{\cancel{(x+3)}}=x-2=g(x), \text{ } x \neq -3.$$ Applying Theorem 1.3.7 produces $$\lim_{ x \to -3}\frac{x^2+x-6}{x+3}$$ $$=\lim_{ x \to -3}(x-2)$$      Apply Theorem 1.3.7 \(=-5\)      Use direct substitution. This result is displayed in Figure 1.3.3. Note the graph for \(f\) coincides with the graph for \(g(x)=x-2\) except for the gap in \(f\) at the point (\(-3,-5)\). In Example 1.3.7 direct substitution produced the meaningless fraction \(0/0\). An expression such as \(0/0\) is called an indeterminate form because fraction is useless in determining the limit. Rewrite the fraction so that the new denominator does not have 0 as its limit. One way to do this is to divide out like factors. Another way is to use the rationalizing technique below.

The Rationalizing Technique

The limit for \(f(x)\) as \(x\) approaches 0 is \(\frac{1}{2}\). Figure 1.3.4

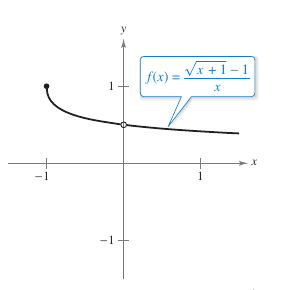
This technique involves rationalizing the numerator in a fractional expression. Recall that rationalizing the numerator mean multiplying the numerator and denominator by the conjugate of the numerator. For example, to rationalize the numerator for $$\frac{\sqrt{x}+4}{x} $$ multiply the numerator and denominator by the conjugate of \(\sqrt{x}+4\), which is $$\sqrt{x}-4. $$ Example 1.3.7 Rationalizing Technique Find the limit: $$\lim_{x \to 0}\frac{\sqrt{x+1}-1}{x}. $$ Solution Direct substitution produces the indeterminate form \(0/0\). For this case rewrite the fraction by rationalizing the numerator. $$\frac{\sqrt{x+1}-1}{x} $$ $$= \left (\frac{\sqrt{x+1}-1}{x}\right)\left (\frac{\sqrt{x+1}+1}{\sqrt{x+1}+1}\right) $$ $$= \frac{(x+1)-1}{x(\sqrt{x+1}+1)}$$ $$=\require{cancel} \frac{\cancel{x}}{\cancel{x}(\sqrt{x+1}+1)}$$ $$=\frac{1}{\sqrt{x+1}+1},\text{ } x \neq 0$$ Using Theorem 1.3.7 evaluates the limit. 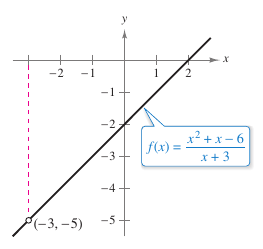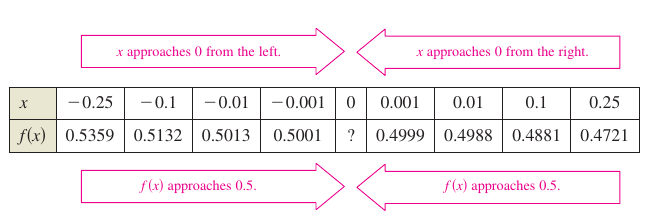$$\lim_{x \to 0}\frac{\sqrt{x+1}-1}{x} $$ $$=\lim_{x \to 0}\frac{1}{\sqrt{x+1}-1} $$ $$=\frac{1}{1+1}$$ $$=\frac{1}{2}$$ A table or graph add additional evidence that the limit is \(\frac{1}{2}\). See Figure 1.3.4 and the table below. Table 1.3.1

The Squeeze Theorem

The Squeeze Theorem Figure 1.3.5 A circular sector is used to prove Theorem 1.3.8 Figure 1.3.6

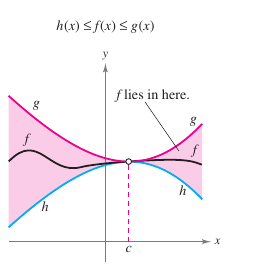
The limit for a function is squeezed between two other functions. Each has the same limit at a given \(x\)-value, as shown in Figure 1.3.5. Theorem 1.3.8 The Squeeze Theorem If \(h(x) \leq f(x) \leq g(x)\) for all \(x\) in an open interval containing \(c\), except possibly at \(c\) itself, and if $$\lim_{x \to c} h(x)=L=\lim_{x \to c} g(x)$$ the \(\lim_{x \to c} f(x)\) exists and is equal to \(L\). Theorem 1.3.9 Two Special Trigonometric Limits $$\text{1. }\lim_{x \to c} \frac{\sin x}{x}=1$$ $$\text{2. 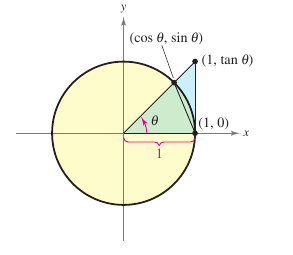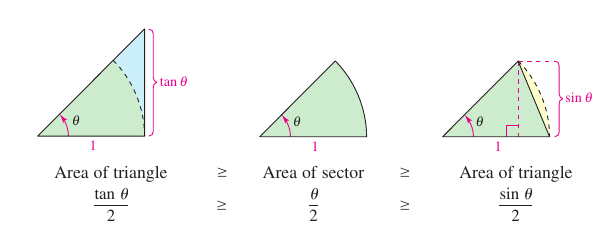}\lim_{x \to c} \frac{1-\cos x}{x}=0$$ Proof The proof for the second limit is left as an exercise. To avoid confusion with how \(x\) is used the proof for the first limit is presented using the variable \(\theta\), where \(\theta\) is an acute positive angle measured in radians. Figure 1.3.8 shows a circular sector that is squeezed between two triangles. Multiplying each expression by \(2/\sin \theta\) produces $$ \frac{1}{\cos x}\geq \frac{\theta}{\sin \theta} \geq 1$$ and taking reciprocals and reversing the inequalities yields $$\cos \theta \leq \frac{\sin \theta}{\theta} \leq 1.$$ Because \(\cos \theta =1\) and \((\sin \theta)/\theta=[\sin)-\theta)]/(-\theta)\), this inequality is valid for all nonzero \(\theta\) on the open interval \((-\pi/2,\pi/2)\). Finally, because \(\lim_{\theta \to 0} \cos \theta=1\) and \(\lim_{\theta \to 0} 1=1\), applying the Squeeze Theorem produces \(\lim_{\theta \to 0}(\sin 0)/ \theta=1\).

Example 1.3.8 A Limit Involving a Trigonometric Function

The limit for \(f(x)\) as \(x\) approaches 0 is 1. Figure 1.3.7

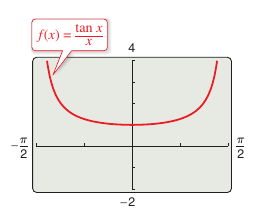
Find the limit: $$\lim_{x \to 0} \frac{\tan x}{x}.$$ Solution Direct substitution yields the indeterminate form 0/0. To solve this problem write \(\tan x\) as \((\sin x)/(\cos x)\) and obtain $$\lim_{x \to 0} \frac{\tan x}{x}= \lim_{x \to 0} \left ( \frac{\sin x}{x} \right ) \left ( \frac{1}{\cos x}\right ).$$ Because $$\lim_{x \to 0} \frac{\sin x}{x}=1$$ and $$\lim_{x \to 0} \frac{1}{\cos x}=1$$ obtains $$\lim_{x \to 0} \frac{\tan x}{x}$$ $$= \lim_{x \to 0} \left ( \frac{\sin x}{x} \right ) \left ( \lim_{x \to0}\frac{1}{\cos x}\right )$$ \(=(1)(1)\) \(=1.\) As shown in Figure 1.3.7.

Example 1.3.9 A Limit Involving a Trigonometric Function

The limit for \(g(x)\) as \(x\) approaches 0 is 4. Figure 1.3.8

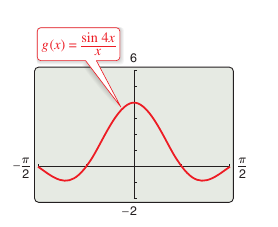
Find the limit: $$\lim_{x \to 0} \frac{\sin 4x}{x}.$$ Solution Direct substitution yields the indeterminate form 0/0. To solve this problem rewrite the limit as $$\lim_{x \to 0} \frac{\sin 4x}{x}= 4 \left (\lim_{x \to 0} \frac{\sin 4x}{4x} \right ).$$     Multiply and divide by 4. Let \(y=4x\) and observe that \(x\) approaches 0 if and only if \(y\) approaches 0 the expression can be written as $$\lim_{x \to 0} \frac{\sin 4x}{x}$$ $$= 4 \left (\lim_{x \to 0} \frac{\sin 4x}{4x} \right )$$ $$= 4 \left (\lim_{y \to 0} \frac{\sin y}{y} \right )$$     Let \(y=4x\). \(=4(1)\)     Apply Theorem 1.3.9(1) \(=4.\) As shown in Figure 1.3.8.

Internal Links

Parent Article: Calculus I 01 Limits and Their Properties