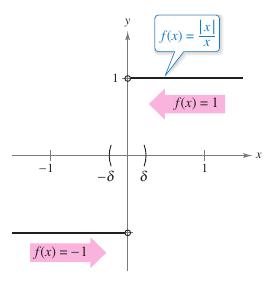Calculus I 01.02 Finding Limits Graphically and Numerically

Previous	Calculus I 01.01 What is Calculus?
Next	Calculus I 01.03 Evaluating Limits Analytically

Finding Limits Graphically and Numerically

• Estimate a limit using a numerical or graphical approach.
• Learn why a limit may not exist.
• A formal definition the limit.

An Introduction to Limits

The limit for \(f(x)\) as \(x\) approaches 1 is 3. Figure 1.2.1

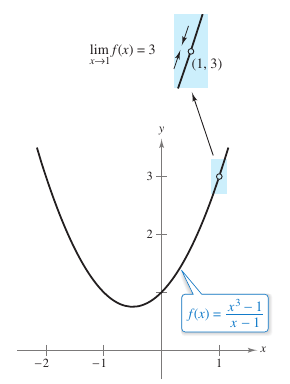
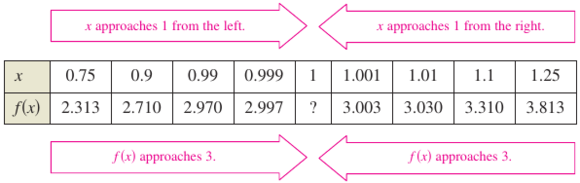
Sketch the graph for $$ f(x)=\frac{x^3-1}{x-1}$$ for values other than \(x=1\). At \(x=1\) the graph's behavior is unknown. Thus the circle in the graph, as shown in Figure 1.2.1. To investigate the graph as it approaches \(x=1\) divide the values for \(x\) into two sets. One approaching from the left and one approaching from the right. As displayed in Table 1.2.1 below. Table 1.2.1 As \(x\) moves arbitrarily close to 1 the result from \(f(x)\) moves arbitrarily close to 3. Calculus notation expresses this idea below: $$\lim_{x \to 1}f(x)=3 $$     This is read as "the limit for \(f(x)\) as \(x\) approaches 1 is 3" An informal definition for the Limit. If \(f(x)\) becomes arbitrarily close to a single number \(L\) as \(x\) approaches \(c\) from either side, then the limit for \(f(x)\) is \(L\). This limit is written as $$\lim_{x \to c}f(x)=L $$

Example 1.2.1 Estimating a Limit Numerically

The limit for \(f(x)\) as \(x\) approaches 0 is 2. Figure 1.2.2

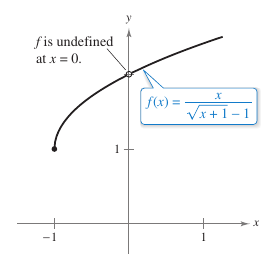
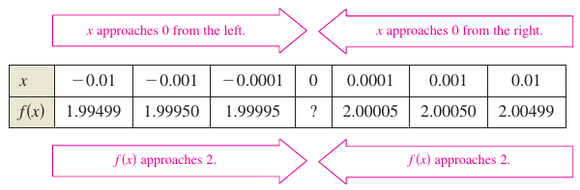
Evaluate the function \(f(x)=x/(\sqrt{x+1}-1)\), as shown in Figure 1.2.2, at several \(x\)-values near 0 and use the result to estimate the limit $$\lim_{x \to 0}\frac{x}{\sqrt{x+1}-1}.$$ Solution Table 1.2.2 describes the values for \(f(x)\) for six \(x\)-values near 0. Table 1.2.2 From the results in Table 1.2.2 the estimated limit is 2. This agrees with the graph for \(f\) in Figure 1.2.2. In Example 1.2.1, note the function is undefined at \(x=0\), and yet \(f(x)\) appears to approach a limit as \(x\) approaches 0. This often happens, and it is important to realize the existence or nonexistence for \(f(x)\) at \(x=c\) has no bearing on the existence of the limit for \(f(x)\) as \(x\) approaches \(c\).

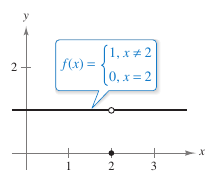
Example 1.2.2 Finding a Limit

The limit for \(f(x)\) as \(x\) approaches 2 is 1. Figure 1.2.3

Find the limit for \(f(x)\) as \(x\) approaches 2, where $$f(x)=\left\{\begin{matrix} 1, & x \neq 2\\ 0, & x=2 \end{matrix}\right.$$ Solution Because \(f(x)=1\) for all \(x\) other than \(x=2\), the estimated limit is 1, as shown in Figure 1.2.3. This limit is written as $$\lim_{x \to 2}f(x)=1.$$ The fact that \(f(2)=0\) has no bearing on the existence or the limit's value as \(x\) approaches 2. For example, as \(x\) approaches 2, the function $$g(x)=\left\{\begin{matrix} 1, & x \neq 2\\ 2, & x=2 \end{matrix}\right.$$ has the same limit as \(f\). In Section 1.2 limits are estimated numerically and graphically. Each approach produces an estimated limit. Section 1.3 describes using analytic techniques for evaluating limits. Throughout the course use this three-pronged approach to solving Calculus problems. 1. Numerical Construct a table with values. 2. Graphical Draw a graph describing the function 3. Analytic Use algebra or calculus

Limits That Fail to Exist

The next three examples describes limits that fail to exist.

Example 1.2.3 Different Right and Left Side Behavior

The \(\lim{x \to 0} f(x)\) does not exist. Figure 1.2.4

Show that the limit $$ \lim_{x \to 0}=\frac{\left | x \right |}{x} $$ does not exist. Solution Consider the graph for the function displayed in Figure 1.2.4 $$ f(x)=\frac{\left | x \right |}{x} .$$ Using Figure 1.2.4 and the definition for absolute value, $$f(x)=\left\{\begin{matrix} 1, & x \neq 2\\ 0, & x=2 \end{matrix}\right.$$ Definition for absolute value. the range for \(x\)-values are $$ \frac{\left | x \right |}{x}=\left\{\begin{matrix} 1, & x \neq 2\\ 0, & x=2 \end{matrix}\right.$$ Thus, no matter how close \(x\) gets to 0, there will be both positive and negative \(x\)-values that yield \(f(x)=1\) or \(f(x)=-1\). Specifically, if \(\delta\) (the lowercase Greek letter delta) is a positive number, then for \(x\)-values satisfying the inequality \(0 < \left | x \right | < \delta\), the values for \(\left | x \right | / x\) classify as Because \( \left | x \right | /x\) approaches a different number from 0's right side than it approaches from the left side, the limit \(\lim_{x \to 0}(\left | x \right | /x)\) does not exist.

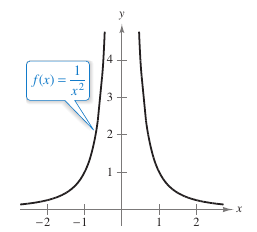
Example 1.2.4 Unbounded Behavior

\(\lim_{x \to 0} f(x)\) does not exist. Figure 1.2.5

Find if the limit for $$ \lim_{x \to 0}\frac{1}{x^2}$$ exists. Solution Consider the graph for the function displayed in Figure 1.2.5 $$ f(x)=\frac{1}{x^2}.$$ In Figure 1.2.5 as \(x\) approaches 0 from either the right or the left, \(f(x)\) increases without bound. This mean that \(f(x)\) grows enormously as \(x\)-values get closer and closer to 0. For example, \(f(x)\) will be greater than 100 when \(x\) is within \(\frac{1}{10}\) of 0. That is, $$0<\left | x \right | <\frac{1}{10} \Rightarrow f(x)= \frac{1}{x^2} > 100.$$ Putting \(f(x)\) over 1,000,000 is done below. $$0<\left | x \right | <\frac{1}{1000} \Rightarrow f(x)= \frac{1}{x^2} > 1,000,000.$$ Because \(f(x)\) does not become arbitrarily close to a single number \(L\) as \(x\) approaches 0 the limit does not exist.

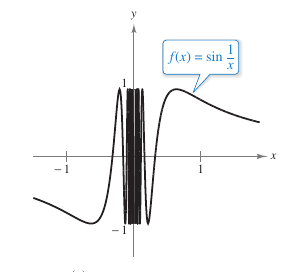
Example 1.2.5 Oscillating Behavior

\(\lim_{x \to 0} f(x)\) does not exist. Figure 1.2.7

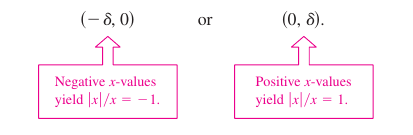
Determine the existence for the limit to $$ \lim_{x \to 0} \sin \frac{1}{x}.$$ Solution Let \(f(x)= \sin \frac{1}{x}\). In Figure 1.2.6 as \(x\) approaches 0 \(f(x)\) oscillates between \(-1\) and 1. Therefore the limit does not exist because no matter how small \(\delta\) becomes, it is possible to choose \(x_1\) and \(x_2\) within \(\delta\) units from 0 such that \(sin(1/x_1=1\) and \(sin(1/x_1=-1\) , as shown in Table 1.2.3. Table 1.2.3

Common Behavior Types Associated with Nonexistent Limits

1. \(f(x)\) approaches a different number from the right side to \(c\) than it approaches from the left side.
2. \(f(x)\) increases or decreases without bound as \(x\) approaches \(c\).
3. \(f(x)\) oscillates between two fixed values as \(x\) approaches \(c\).

There are many other interesting functions that have unusual limit behavior. An often cited one is the Dirichlet function[1]

$$f(x)=\left\{\begin{matrix} 0,&\text{if } x \text{ is rational}\\ 1,& \text{if } x \text{ is irrational} \end{matrix}\right.$$

Because this function has no limit at any real number \(c\), it is not continuous at any real number \(c\). This is described in greater detail in Section 1.4.

A Formal Definition for the Limit

The limit for \(f(x)\) using the \(\epsilon-\delta\) definition as \(x\) approaches \(c\). Figure 1.2.8

Consider the informal definition for limit discussed earlier in this section. 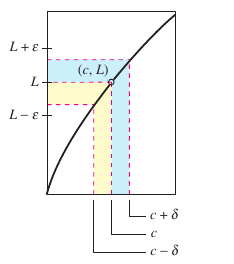If \(f(x)\) becomes arbitrarily close to a single number \(L\) as \(x\) approaches \(c\) from either side, then the limit for \(f(x)\) as \(x\) approaches \(c\) is \(L\), written as $$\lim{x \to c} f(x) = L.$$ The weakness in this definition is that exact meanings have not been given to two phrases “\(f(x) \text{ becomes arbitrarily close to }L\)” and “\(\text{ approaches }c .\)” The first person to assign mathematically rigorous meanings to these phrases was Augustin-Louis Cauchy.[2] His \(\boldsymbol {\varepsilon-\delta}\) limit definition is the standard used today. Figure 1.2.8 displays the definition in simplified form. Let \(\epsilon\) (the lowercase Greek letter epsilon) represent a (small) positive number. Then the phrase “\(f(x)\) becomes arbitrarily close to L” means that “\(f(x)\) becomes arbitrarily close to \(L\) ” means that \(f(x)\) lies on the interval \((L-\epsilon,L+\epsilon)\). Using absolute value this can be written as $$\left | f(x)-L \right | < \epsilon.$$ The phrase “\(x\) approaches \(c\) ” means that there exists a positive number \(\epsilon\) such that \(x\) lies on the interval \((c-\epsilon,c)\) or the interval \((c,c+\epsilon)\). This fact can be concisely expressed by the double inequality $$0<\left | x-c \right | < \epsilon.$$ The first inequality $$0<\left | x-c \right | $$     The distance between \(x\) and \(c\) is more than 0. expresses the fact that \(x \neq c\). The second inequality $$\left | x-c \right | < \epsilon.$$     \(x\) is within \(\epsilon\) units from \(c\). says that \(x\) is within a distance \(\epsilon\) from \(c\).

Definition 1.2.1 Formal Definition for the Limit

Let \(f\) be a function defined on an open interval containing \(c\) (except possibly at \(c\)), and let \(L\) be a real number. The statement

$$ \lim{x \to c} f(x) = L$$

means that for each \(\epsilon > 0\) there exists a \(\epsilon > 0\) such that if

$$\left | x-c \right | < \epsilon.$$

then

$$\left | f(x)-L \right | < \epsilon.$$

This means the limit exists and the limit is \(L\). |} Some functions do not have limits as \(x\) approaches \(c\), but those that do cannot have two different limits as \(x\) approaches \(c\). That is, if the limit for a function exists, then the limit is unique. The next three examples describe the \(\varepsilon-\delta\) limit definition in more detail.

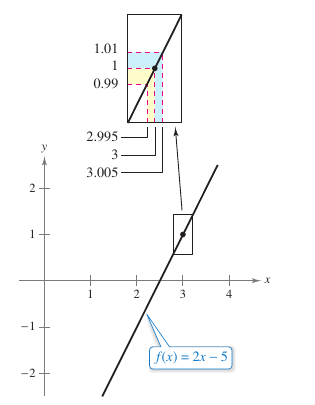
Example 1.2.6 Find a \(\delta\) for a Given \(\epsilon\)

The limit for \(f(x)\) as \(x\) approaches 3 is 1. Figure 1.2.9

Given the limit $$\lim{x \to 3} (2x-5) = 1 $$ find \(\epsilon\) such that $$\left | (2x-5) -1 \right | < 0.01$$ whenever $$0 < \left | x-3 \right | < \epsilon.$$ Solution Epsilon, \(\epsilon\), is given the value \(\epsilon = 0.01\). To find an appropriate \(\delta\), establish a connection between the absolute values $$\left | (2x-5)-1 \right | \text{ and } \left | x-3 \right |.$$ Notice that $$\left | (2x-5)-1 \right | = \left | 2x-6 \right | = 2 \left | x-3 \right |.$$ Because the inequality \(\left | (2x-5)-1 \right | < 0.01\) is equivalent to \(2 \left | x-3 \right | < 0.01\), a good starting value is $$\delta = \frac{1}{2}(0.01)= (0.005).$$ This choice works because $$0 < \left | x-3 \right | < 0.005$$ which implies that $$\left | (2x-5)-1 \right | =2 \left | x-3 \right | = 2 (0.005)=0.01.$$ Figure 1.2.9 displays \(f(x)\) for \(x\)-values within \(3(x \neq 3)\) producing values within 0.01 of 1. Example 1.2.6 produces a \(\delta\)-value for a given \(\epsilon\). This does not prove a limit exists. To prove a limit requires finding a \(\delta\) for any \(\epsilon\). Example 1.2.7 describes this in more detail.

Example 1.2.7 Using the \(\epsilon-\delta\) Limit Definition

The limit for \(f(x)\) as \(x\) approaches 2 is 4. Figure 1.2.10

Us the \(\epsilon-\delta\) limit definition to prove that $$\lim_{x \to 2} (3x-2)=4.$$ Solution Show that for each \(\epsilon >0\), there exists a \(\delta > 0\) such that $$\left | (3x-2)-4\right | < \epsilon$$ whenever $$0< \left | x-2 \right | < \delta.$$ Because the choice for \(\delta\) depends on \(\epsilon\) establish a connection between the absolute values \(\left | (3x-2)-4 \right | \) and \(\left | x-2 \right | \). 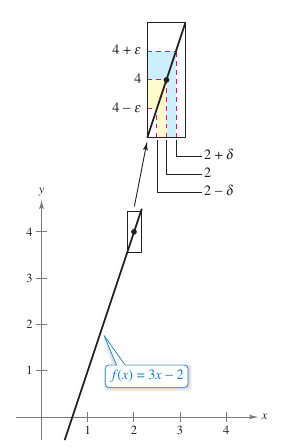$$\left | (3x-2)-4\right | = \left | 3x-6 \right | = 3\left | 3x-2 \right |$$ For a given \(\epsilon > 0\) we'll start with \(\delta=\epsilon/3\). This works because $$0<\left | x-2\right | < \delta = \frac{\epsilon}{3}$$ implies that $$\left | (3x-2)-4\right | = 3\left | x-2 \right | < \frac{\epsilon}{3} = \epsilon.$$ Figure 1.2.10 displays the \(x\)-values within \(\delta\) of \(2(x \neq 2)\), the values for \(f(x)\) are within \(\epsilon\) of 4.

Example 1.2.8 Using the \(\epsilon-\delta\) Limit Definition with a Polynomial Equation

The limit for \(f(x)\) as \(x\) approaches 2 is 4. Figure 1.2.11

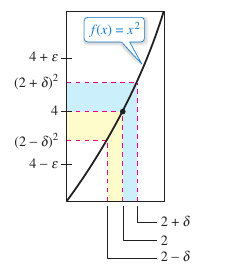
Use the \(\epsilon-\delta\) Limit Definition to prove that $$\lim_{x \to 2} x^2=4.$$ Solution Show that for each \(\epsilon >0\), there exists a \(\delta >0\) such that $$\left |x^2-4 \right | < \epsilon$$ whenever $$0<\left |x-2 \right | < \delta.$$ To find an appropriate \(\delta\), begin with $$\left | x^2-4 \right |=\left | x-2 \right |\left | x+2 \right |.$$ For all \(x\) in the interval (1,3), \(x+2<5\) and thus \(|\left | x+2 \right |<5\). Letting \(\delta\) be the minimum between \(\epsilon/5\) and 1, it follows that, whenever \(0<\left | x-2 \right |<\delta\) produces $$\left | x^2-4 \right |=\left | x-2 \right |\left | x+2 \right |<\left ( \frac{\epsilon}{5} \right )(5)=\epsilon.$$ Figure 1.2.11 displays \(x\)-values within \(\delta\) of \(2(x\neq2)\), the values for \(f(x)\) are within \(\epsilon\) of 4.

Internal Links

Parent Article: Calculus I 01 Limits and Their Properties