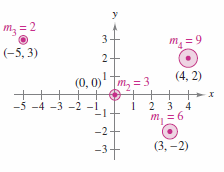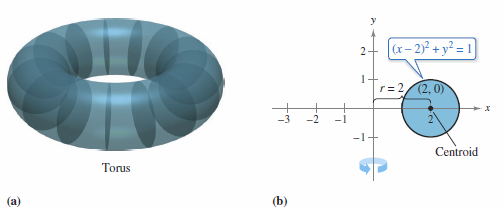Calculus II 07.06 Moments Centers of Mass and Centroids

Previous	Calculus II 07.05 Work
Next	Calculus II 07.07 Fluid Pressure and Fluid Force

7.6 Moments, Centers of Mass, and Centroids

• Understand the definition for mass.
• Find the center of mass in a one-dimensional system.
• Find the center of mass in a two-dimensional system.
• Find the center of mass of a planar lamina.
• Use the Theorem of Pappus to find the volume for a rotated solid.

Mass

Mass[1] measures a body’s resistance to changes in motion. A body's mass is constant, no matter how strong the gravitational field around it. The weight for a body depends on the local gravitational field. Since the local gravitational field is, to an acceptable tolerance, constant, mass is often measured as weight. Force and mass are related by the equation

$$\text{Force} = (mass)(acceleration).$$

Table 7.6.1 describes commonly used measures for mass and force, with their conversion factors.

Table 7.6.1 Mass and Force
Measurement System	Mass Measure	Force Measure
US	Slug	\(Pound=(slug)(ft/sec^{2})\)
International	Kilogram	\(Netwon=(kilogram)(m/sec^{2})\)
C-G-S	Gram	\(Dyne=(gram)(cm/sec^{2})\)
1 pound = 4.48 newtons 1 newton = 0.2248 pounds 1 dyne = 0.000002248 pound 1 dyne = 0.00001 newton 1 slug = 14.59 kilograms 1 kilogram = 0.06852 slug 1 gram = 0.00006852 slut 1 foot = 0.3048 meter

Example 7.6.1 Mass on the Earth's Surface

Find the mass (in slugs) for an object whose weight, at sea level, is 1 pound on Earth.
Solution Use 32 feet per second per second as the acceleration due to gravity.

\(Mass\)	$$= \frac{force}{acceleration} $$	Force =(mass)(acceleration)
	$$ = \frac{1\: pound}{32\: feet\: per\: second\: per\: second} $$
	$$ =0.03125 \frac{pound}{foot\: per\: second\: per\: second} $$
	\( = 0.03125\:slug\)

On Earth’s surface, this measurement is called a pound mass.

Mass Center in a One-Dimensional System

The seesaw will balance when the left and the right moments are equal. Figure 7.6.1

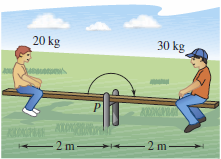
Consider two moment types — the moment about a point and the moment about a line. In an ideal situation where a mass \(m\) is concentrated at a point. If \(x\) is the distance between this point mass and another point \(P\), then the moment of \(m\) about the point \(P\) is $$\text{Moment}= mx$$ and \(x\) is the length of the moment arm. In Figure 7.6.1 the seesaw has a child with a 20 kilogram mass 2 meters to fulcrum \(P\)'s left, and a child with a 30 kilogram mass 2 meters to fulcrum \(P\)'s right. Given no support under either child the seesaw will rotate clock-wise and lower the heavier child on the right. This rotation occurs because the moment produced by the child on the left is less than the moment produced by the child on the right. 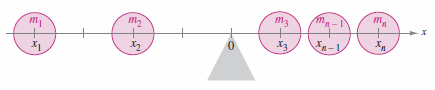Left moment = (20)(2) = 40 kilograms-meters Left moment = (30)(2) = 60 kilograms-meters Balancing the seesaw requires that both moments be equal. On method is to equalize the weights. Another is to change position relative to the fulcrum. If the heavier child moved to a position \(1\:\frac{1}{3}\) meters from the fulcrum, then the seesaw would balance because each child would produce a 40 kilogram-meter moment. For the general solution introduce a coordinate line with the origin on the fulcrum, as shown in Figure 7.6.2, with \(n\) point masses along the \(x\)-axis. The tendency to rotate about the origin is called the moment about the origin, denoted by \(M_{0}\), and is defined as summing the product \(m_{i}x_{i}\) for \(n\) times. This can be written out as $$M_{0}=m_{1}x_{1}+m_{2}x_{2}+\cdots +m_{n}x_{n}.$$ If \(M_{0}\) is 0, the system is in equilibrium. If \(M_{0}\) < 0 the system rotates to the left. If \(M_{0}\) > 0 the system rotates to the right. If \(m_{1}x_{1}+m_{2}x_{2}+\cdots +m_{n}x_{n}=0\), then the system is in equilibrium.. Figure 7.6.2 For a system that is not in equilibrium, the center of mass is defined as the point \(\bar{x}\) at which the fulcrum could be relocated to attain equilibrium. If the system were translated \(\bar{x}\) units, then each coordinate \(x_{i}\) would become \((x_{i}-\bar{x})\) and because the translated system has a moment equal to zero, you have $$\sum^{n}_{i=1} m_{i} \left( x_{i}-\bar{x} \right) =\sum^{n}_{i=1} m_{i}x_{i} -\sum^{n}_{i=1} m_{i}\bar{x} =0.$$ Solving for \(\bar{x}\) produces $$ \bar{x} = \frac{ \sum_{i=1}^{n} m_{i}x_{i} }{ \sum_{i=1}^{n} m_{i}} = \frac{\text{moment of system about origin}}{\text{total system mass}} $$ When \(m_{1}x_{1}+m_{2}x_{2}+\cdots +m_{n}x_{n}=0\), the system is in equilibrium.

Definition 7.6.1. Moments and Center of Mass: One-Dimensional System

Let the point masses \(m_{1},m_{2},...,m_{n} \) be located at \(x_{1},x_{2},...,x_{n} \).

1. The moment about the origin is

$$M_{0}= m_{1}x_{1}+m_{2}x_{2}+\cdots +m_{n}x_{n} $$

2. The mass center is

$$\bar{x} = \frac{M_{0}}{m} $$

where \(m=m_{1} + m_{2}+ \cdots +m_{n} \) is the system's total mass.

Example 7.6.2 The Mass Center in a Linear System

Find the center of mass of the linear system shown in Figure 7.6.3.

Figure 7.6.3

Solution The moment about the origin is

\(M_{0}\)	\(= m_{1}x_{1}+m_{2}x_{2}+m_{3}x_{3}+m_{4}x_{4}\)
	\(=10(-5)+15(0)+5(4)+10(7)\)
	\(=-50+0+20+70=40.\)

Because the total system mass is

$$m=10+15+5+10=40$$

The mass center is

$$\bar{x}=\frac{M_{0}}{m}=\frac{40}{40}=1.$$

Definition 7.6.2 Moment for a Force[2]

Moment of Force, or Torque, is the tendency for a force to rotate an object about an axis, fulcrum, or pivot. The mass center is called the center of gravity. Consider a system with point masses \( m_{1}+m_{2}+\cdots+m_{n}\) that is located at \( x_{1}+x_{2}+\cdots+x_{n}\). Referring back to \( \text{Force} = (mass)(acceleration)\) discussed earlier, the system's total force is

$$F= m_{1}a+m_{2}a+ \cdots + m_{n}a =ma. $$

The torque (moment) about the origin is

$$T_{0}= (m_{1}a)x_{1}+(m_{2}a)x_{2}+ \cdots + (m_{n}a)x_{n} =M_{0}a. $$

and the center of gravity is

$$ \frac{T_{0}}{F}=\frac{M_{0}a}{ma}=\frac{M_{0}}{m}=\bar{x} $$

In this system the centers for gravity and mass have the same location.

The Mass Center in a Two-Dimensional System

In a two-dimensional system, there are moments about the \(y\)-axis \(M_{y}\) and the \(x\)-axis \(M_{x}\). Figure 7.6.4

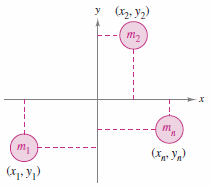
Consider a system with masses located on the \(xy\)-plane at points \((x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n})\) as shown in Figure 7.6.4. Two moments are defined - one with respect to the \(x\)-axis and one with respect to the \(y\)-axis. For higher dimensions there is one moment per axis. A system's masses in the plane can be taken about any horizontal or vertical line. In general, the moment about a line is the masses times the directed distances summed for every point on the line. \(\text{Moment}= m_{1}(y_{1}-b)+m_{2}(y_{2}-b)+ \cdots +m_{n}(y_{n}-b)\) Horizontal line \(y=b\) \(\text{Moment}= m_{1}(x_{1}-a)+m_{2}(x_{2}-a)+ \cdots +m_{n}(x_{n}-a)\) Horizontal line \(x=a\)

Definition 7.6.2 Mass Center and Moment: Two-Dimensional System

Let the point masses \(m_{1},m_{2},...,m_{n}\) be located at \((x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n})\).

1. The moment about the \(y\)-axis is

$$M_{y}= m_{1}x_{1}+m_{2}x_{2}+ \cdots + m_{n}x_{n} $$

2. The moment about the \(x\)-axis is

$$M_{x}= m_{1}y_{1}+m_{2}y_{2}+ \cdots + m_{n}y_{n}$$

3. The mass center \((\bar{x},\bar{y})\) (or gravity center) is

$$\bar{x}=\frac{ M_{y}}{m} \text{ and } \bar{y}=\frac{M_{x}}{m} $$

where

$$m=m_{1}+m_{2}+ \cdots + m_{n} $$

is the system's total mass.

Example 7.6.3 The Mass Center in a Two-Dimensional System

Figure 7.6.5

Find the mass center for a system with point masses \(m_{1}=6\),\(m_{2}=3\),\(m_{3}=2\), and \(m_{4}=9\), located at (3,-2), (0,0), (-5,3), and (4,2) as shown in Figure 7.6.5. Solution \(m\) =6 +3 +2 +9 =20 Mass \(M_{y}\) =6(3) +3(0) +2(-5) +9(4) =44 Moment about \(y\)-axis \(M_{x}\) =6(-2) +3(0) +2(3) +9(2) =12 Moment about \(x\)-axis This produces $$\bar{x}=\frac{M_{y}}{m}=\frac{44}{20}=\frac{11}{5}$$ and $$\bar{y}=\frac{M_{x}}{m}=\frac{12}{20}=\frac{3}{5}.$$ The mass center is $$\left( \frac{11}{5},\frac{3}{5} \right).$$

Mass Center for a Planar Lamina

The mass center, \((\bar{x},\bar{y})\), for a planar lamina has a balancing point at the circle's center or the rectangle's center. Figure 7.6.6 Planar lamina with uniform density. Figure 7.6.7

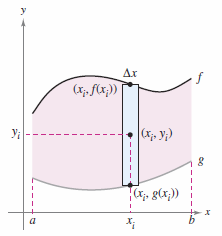
A thin, flat plate with a constant density is called a planar lamina as shown in Figure 7.6.6. For planar laminas density is the mass per area unit and is denoted by \(\rho\) the lowercase Greek letter rho. Consider the irregular planar lamina region with a uniform density \(\rho\) and bounded by \(y=f(x)\), \(y=g(x)\), and \(a\le x \le b\) shown in Figure 7.6.7. It's mass is \(m\) = (density)(area) $$= \rho {\displaystyle \int_{a}^{b} } \left[f(x)-g(x) \right]\:dx =\rho A$$ where \(A\) is the region's area. To find the region's mass center, partition the interval \([a,b]\) into \(n\) subintervals with equal width \(\delta x\). Let \(x_{i}\) be the center for the \(i\)th subinterval. The rectangle height \(h\) for each subinterval is \(h=f(x_{i})-g(x_{i})\). Because the rectangle's density is \(\rho\), its mass is $$m_{i}=(\text{density})(\text{area})=\color{red}{\underbrace{\color{black}{\rho}}_{\color{red}{\text{Density}}}} \color{red}{\underbrace{\color{black}{[f(x_{i})-g(x_{i})]}}_{\color{red}{\text{Height}}}} \color{red}{\underbrace{\color{black}{\Delta \: x}}_{\color{red}{\text{Width}}}}.$$ The rectangle's mass is centered at (x,y) with the directed distance from the \(x\)-axis to any point \((x_{i},y_{i})\) is \(y_{i}= [f(x_{i})+g(x_{i})]/2\). The moment for \(m_{i}\) about the \(x\)-axis is Moment \( =(\text{mass})(\text{distance})\) \(= m_{i}y_{i}\) $$=\rho \left[ f(x_{i})+g(x_{i}) \right] \Delta \:x \: \left[ \frac{f(x_{i})+g(x_{i})}{2} \right] .$$

Definition 7.6.3 Moments and Mass Center for a Planar Lamina

Sum the moments and push the limit to \(n \to \infty \) produces Definition 7.6.3.
Let \(f\) and \(g\) be continuous functions such that \(f(x) \geq g(x)\) on \([a,b]\). Let a planar lamina with uniform density \(\rho\) be bounded by \(y=f(x)\), \(y=g(x)\), and \(a\leq x \leq b\).

1. The moment about the \(x\) and \(y\)-axes are

$$M_{x}= \rho \int_{a}^{b} \left[ \frac{f(x_{i})+g(x_{i})}{2} \right] \left[ f(x_{i})+g(x_{i}) \right] \:dx $$

$$M_{y}= \rho \int_{a}^{b}x \left[ f(x_{i})+g(x_{i}) \right] \:dx $$

2. The mass center \((\bar{x},\bar{y})\) is given by \(\bar{x} = \frac{M_{y}}{m}\) and \(\bar{y} = \frac{M_{x}}{m}\), where

$$ m=\rho \int_{a}^{b}x \left[ f(x_{i})+g(x_{i}) \right] \:dx $$ is the lamina's mass.

Example 7.6.4 The Mass Center for a Planar Lamina

Moment in rectangle \(f(x)\). Figure 7.6.8 Planar lamina with uniform density. Figure 7.6.9

Find the mass center for a lamina with uniform density \(\rho\) and bounded by \(f(x)=4-x^{2}\) and the \(x\)-axis as shown in Figure 7.6.8. Solution Because the mass center lies on the symmetric axis \(\bar{x}=0\). Plugging \(f(x)\) into Definition 7.6.3 produces the mass \(m\) $$ = \rho \int_{-2}^{2} \left( 4-x^{2} \right)\: dx $$ $$=\rho \left[ 4x-\frac{x^{3}}{3} \right]_{-2}^{2}=\frac{32 \rho}{3} .$$ Find the moment about the \(x\)-axis by placing a representative rectangle in the region, as shown in Figure 7.6.8. The distance from the \(x\)-axis to the rectangle's center is $$y_{i} = \frac{f(x)}{2}= \frac{4-x^{2}}{2}.$$ Because the rectangle's mass is $$\rho f(x) \: \Delta x = \rho (4-x^{2})\: \Delta x $$ which produces \(M_{x}\) $$ = \rho \int_{-2}^{2}\frac{(4-x^{2})}{2} \: dx $$ $$ = \frac{ \rho }{2} \int_{-2}^{2} \left( 16-8x^{2}+ x^{4} \right) \: dx $$ $$ = \frac{ \rho }{2} \left[ 16x-\frac{8x^{3}}{3}+ \frac{x^{5}}{5} \right]_{-2}^{2}= \frac{256 \rho}{15} $$ and \(\bar{y}\) is $$\bar{y} = \frac{M_{x}}{m}= \frac{256 \rho / 15}{32 \rho /3} = \frac{8}{5} .$$ The mass center, and balancing point, for the lamina is \( (0, \frac{8}{5}) \), as shown in Figure 7.6.9.

The density \( \rho \) in Example 7.6.4 is a common factor for the moments and mass. The mass center for a lamina with uniform density depends only on its shape and not its density. For this reason, the point

\(\left( \bar{x},\bar{y} \right)\)    Mass Center or Centroid

is sometimes called the mass center for a region on the plane, or the Centroid for the region. To find a region's Centroid on a plane, assume the region has a constant density \(\rho = 1 \) and compute the corresponding mass center.

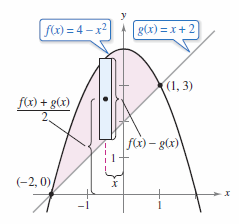
Example 7.6.5 The Centroid for a Plane Region

Figure 7.6.10

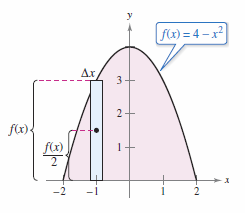
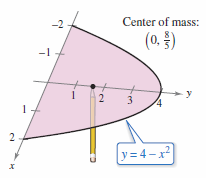
Find the centroid for the plane region bounded by \(f(x)=4-x^{2}\) and \(g(x)=x+2\). Solution The graphs intersect at (-2,0) and (1,3), as shown in Figure 7.6.10. The area is $$A= \int_{-2}^{1} \left[f(x)-g(x) \right] \: dx = \int_{-2}^{1} (2-x-x^{2}) \: dx = \frac{9}{2}. $$ The centroid \((\bar{x},\bar{y})\) has the coordinates. \( \bar{x} \) $$ = \frac{1}{A} \int_{-2}^{1} x \left[ (4-x^{2})-(x+2) \right] \: dx $$ $$ = \frac{2}{9} \int_{-2}^{1} (-x^{3}-x^{2}+2x) \: dx $$ $$ = \frac{2}{9} \left[ - \frac{x^{4}}{4}-\frac{x^{3}}{3}+x^{2} \right]_{-2}^{1} = -\frac{1}{2}$$ \( \bar{y} \) $$ = \frac{1}{A} \int_{-2}^{1} \times \left[ \frac{(4-x^{2})+(x+2)}{2} \right] \left[(4-x^{2})-(x+2) \right] \: dx $$ $$ = \frac{2}{9} \left( \frac{1}{2} \right) \int_{-2}^{1} \left(-x^{2}+x+6 \right) \left(-x^{2}-x+2 \right) \: dx $$ $$= \frac{1}{9} \int_{-2}^{1} \left( -x^{4}-9x^{2}-4x+12 \right) \: dx $$ $$ = \frac{1}{9} \left[ \frac{x^{5}}{5}-3x^{3}-2x^{2}+12x \right]_{-2}^{1}= \frac{12}{5} $$ The centroid for the region is $$ \left( \bar{x},\bar{y} \right) = \left( -\frac{1}{2},\frac{12}{5} \right).$$

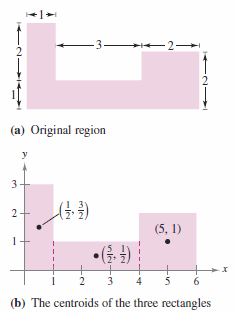
Example 7.6.6 The Centroid for a Simple Plane Region

Figure 7.6.11

Find the centroid for the region shown in Figure 7.6.11(a). Solution Lay the region upon an \(xy\)-coordinate grid with the base even with the \(x\)-axis and the left side even with the \(y\)-axis, as shown in Figure 7.6.11(b). Three rectangles emerge with their own centroids at $$ \left( \frac{1}{2},\frac{3}{2} \right), \: \left( \frac{5}{2},\frac{1}{2} \right) \text{, and }(5,1).$$ Put the three points and the region's area into the following formula: $$\bar{x}$$ $$= \frac{(x_{1})(\text{ rectangle one's area})+(x_{2})(\text{rectangle two's area})+(x_{3})(\text{rectangle three's area}) }{\text{region's area}} $$ $$\bar{y}$$ $$= \frac{(y_{1})(\text{rectangle one's area})+(y_{2})(\text{rectangle two's area})+(y_{3})(\text{rectangle three's area}) }{\text{region's area}} $$ \(A\) \( = \text{ region's area } =3+3+4=10\) \(\bar{x}\) $$ = \frac{(1/2)(3)+(5/2)(3)+(5)(4) }{10} = \frac{29}{10}=10 $$ \(\bar{y}\) $$ = \frac{(3/2)(3)+(1/2)(3)+(1)(4) }{10} = \frac{10}{10}=1 $$ The centroid for the region is (2.9,1). Notice this is not the average for all three rectangle centroids. The general formula is $$ \bar{x}=\frac{(x_{1})(\text{sub area 1})+(x_{2})(\text{sub area 2})+ \cdots+(x_{n})(\text{sub area }\:n)}{\text{region's total area}} $$ $$ \bar{y}=\frac{(y_{1})(\text{sub area 1})+(y_{2})(\text{sub area 2})+ \cdots+(y_{n})(\text{sub area }\:n)}{\text{region's total area}} $$ where \(n\) are the sub regions.

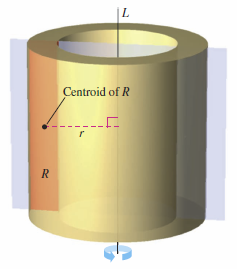
Theorem 7.6.1 Theorem of Pappus

The final topic in this section is a useful theorem credited to Pappus of Alexandria[3] (ca. 300 A.D.), a Greek mathematician whose eight-volume Mathematical Collection is a record of much of classical Greek mathematics. You are asked to prove this theorem in Chapter 14 Multiple Integration.

The volume \(V\) is \(2 \pi r A\), where \(A\) is the area for the region \(R\). Figure 7.6.12

Let \(R\) be a region in a plane and let \(L\) be a line in the same plane such \(L\) that does not intersect the interior of : \(R\) as shown in Figure 7.6.12. If \(r\) is the distance between the centroid for \(R\) and the line, then the volume \(V\) is the solid formed by revolving \(R\) about the line is $$V = 2\pi r A $$ where \(A\) is the area of \(R\). (Note that \(2\pi r A \) is the distance traveled by the centroid as the region is revolved about the line.) The Theorem of Pappus can be used to find a torus volume, as shown in Example 7.6.7. Recall that a torus is a doughnut-shaped solid formed by revolving a circular region about a line that lies in the same plane as the circle (but does not intersect the circle).

Example 7.6.7 Using the Theorem of Pappus to find a Volume

Find the volume for the torus shown in Figure 7.6.13(a), which was formed by revolving the circular region bounded by

$$ (x-2)^{2}+y^{2}=1 $$

about the \(y\)-axis, as shown in Figure 7.6.13(b).

Figure 7.6.13

Solution Figure 7.6.13(b) shows the centroid for the circular region is (2,0). This makes the distance between the centroid and the \(y\)-axis

\(r=2\)

Because the area for the circular region is \(A=\pi\), the torus volume is

\(V\)	\(=2 \pi r A\)
	\(=2 \pi (2)(\pi)\)
	\(= 4 \pi^{2}\approx 39.5\)

Internal Links

Parent Article: Calculus II 07 Integration Applications