Calculus II 07.07 Fluid Pressure and Fluid Force

Previous	Calculus II 07.06 Moments Centers of Mass and Centroids
Next	Calculus II 08 Integration Techniques

7.7 Fluid Pressure and Fluid Force[1][2]

• Find fluid pressure and fluid force.

At sea level 15 pound presses on the one inch square and one kilogram presses on the one centimeter square. Figure 7.7.1

Pressure is the force on a body's surface area. It is measured in pounds per square inch or kilograms per square centimeter. At sea level the atmospheric pressure is 15 pounds per square inch. At 30 feet below sea level the pressure is 30 pounds per square inch.

Definition 7.7.1 Fluid Pressure

The pressure on an object at depth \(h\) in a liquid is

$$\text{Pressure}= P = wh$$

where \(w\) is the liquid's weight-density[3] per volume unit.
Below are weight-densities for common fluids in pounds per cubic foot.

Ethyl alcohol	49.4
Gasoline	41.0-43.0
Glycerin	78.6
Kerosene	51.2
Mercury	849.0
Seawater	64.0
Fresh Water	62.4

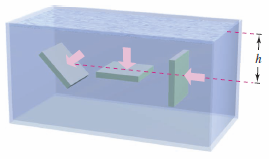
When calculating fluid pressure, you can use an important physical law called Pascal’s Principle[4], named after the French mathematician Blaise Pascal[5]. Pascal’s Principle states that the pressure exerted by a fluid at a depth \(h\) is transmitted equally in all directions. Figure 7.7.2 show the pressure at each depth is the same for all three objects. The fluid force on a submerged horizontal surface with area \(A\) is

$$\text{Fluid force}=F=PA=(\text{pressure})(\text{area}). $$

The pressure at \(h\) is the same for all three objects.
Figure 7.7.2

Example 7.7.1 Fluid Force on a Submerged Sheet

The fluid force on a horizontal metal sheet is equal to the fluid pressure times the area. Figure 7.7.3

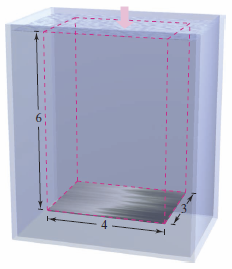
Find the fluid force on a rectangular metal sheet measuring 3 feet by 4 feet that is submerged in 6 feet of water, as shown in Figure 7.7.3. Solution Because the weight-density of water is 62.4 pounds per cubic foot and the sheet is submerged in 6 feet of water, the fluid pressure is \(P\) = (62.4)(6) \(P=wh\) = 374.4 pounds per square foot. Because the sheet's total area is \(A\)=(3)(4) = 12 square feet, the fluid force is \(F\) \(=PA\) $$= \left( 374.4 \frac{\text{pounds}}{\text{square feet}} \right) (\text{12 square feet}) = 4492.8\:\text{ pounds }$$ The fluid's width does not matter, only the depth matters. The fluid force is the same at the same depth in a lake or ocean.

Calculus is needed to find the fluid force exerted on a vertical surface. Figure 7.7.4

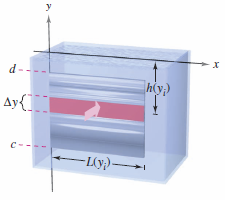
In Example 7.7.1 calculus was not needed because the entire surface was all at the same depth and thus all the pressure exerted on the body was the same. Consider a surface that is submerged vertically in a fluid. This problem requires calculus because the pressure is not constant over the surface. Consider a vertical plate that is submerged in a fluid of weight-density \(w\), as shown in Figure 7.7.4. To find the total force against one side from depth \(c\) to depth \(d\), divide the interval \([c,d]\) into \(n\) subintervals with width \(\Delta y\). Take a rectangle \(y_{i}\) with width \(\Delta y\) and length \(L(y_{i})\), where \(y_{i}\) is the \(i\)th subinterval. The force against this representative rectangle is \(\Delta F\) \( = w(\text{depth})(\text{area})\) \( = w(y_{i})L(y_{i})\Delta \:y\) The force against \(n\) such rectangles is $$ \sum_{i=1}^{n} \: \Delta F_{i} = w \sum_{i=1}^{n} h(y_{i})L(y_{i})\Delta y .$$ Note that \(w\) is a constant and is factored from the summation. Taking the limit as \(\| \Delta \| \to 0 (n \to \infty ) \) produces Definition 7.7.2.

Definition 7.7.2 Force Exerted by a Fluid

The force \(F\) exerted by a fluid with a constant weight-density \(w\)
against a submerged vertical plane region from \(y=c\) to \(y=d\) is

$$F = w \lim_{ \| \Delta \| \to 0} \sum_{i=1}^{n} h(y_{i})L(y_{i})\Delta y $$

$$ = w \int_{c}^{d} h(y)L(y)\: dy $$

where \(h(y)\) is the depth in the fluid at \(y\) and \(L(y)\) is the region's horizontal length at \(y\).

Example 7.7.2 Fluid Force on a Vertical Surface

Figure 7.7.5

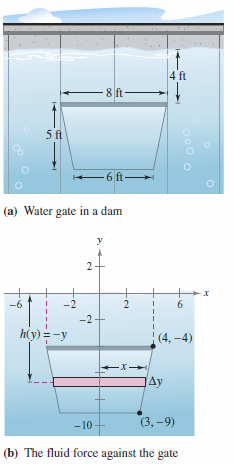
A vertical gate in a dam is shaped like an isosceles trapezoid, 8 feet across the top and 6 feet across the bottom, with a height of 5 feet, as shown in Figure 7.7.5(a). What is the fluid force on the entire gate when the gate's top is submerged 4 feet below the water? Solution For this problem the axes can be set most anywhere. For simplicity we'll lay the \(x\)-axis across the water's surface and the \(y\)-axis through the gate's middle as shown in Figure 7.7.5(b). This makes the depth in feet $$ \text{Depth} = h(y) = -y.$$ To find the gate's length \(L(y)\) at depth \(y\), find the equation for the gate's right side in \(y\) terms, then multiply \(x\) by 2. The line for the right side pass is anchored at points (3,-9) and (4,-4). The equation is \(y-(-9) \) $$= \frac{-4-(-9)}{4-3} (x-3) $$ \( y+9 \) \(=5(x-3) \) \( y \) \(=5x-24 \) \( x \) $$= \frac{y+24}{5} .$$ Figure 7.7.5(b) shows the length at \(y\) is $$\text{Length}=2x=\frac{2}{5}(y+24)=L(y) $$ By integrating from \(y=-9\) to \(y=-4\) the fluid force is \(F\) $$ = w \int_{c}^{d} h(y)L(y)\: dy $$ $$= 62.4\: \int_{-9}^{-4} (-y) \left( \frac{2}{5} \right) (y+24) \: dy $$ $$(= 62.4\:\left( \frac{2}{5} \right) \int_{-9}^{-4} (y^{2}+24y) \: dy $$ $$= 62.4\:\left( \frac{2}{5} \right) \left[ \frac{y^{3}}{3}+12y^{2} \right]_{-9}^{-4} $$ $$= 62.4\: \left( \frac{2}{5} \right) \left( \frac{-1675}{3} \right) $$ = 13,936 pounds.

• Find a really good Fluid Force Submarine example

Example 7.7.3 Fluid Force on a Submarine

Figure 7.7.6

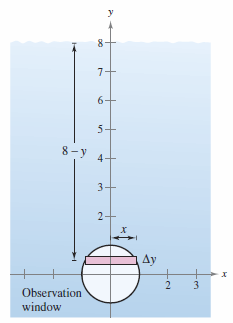
A circular observation window on a submarine has a one foot radius, and the window's center is 8 feet below sea level, as shown in Figure 7.7.6. What is the fluid force on the window? Solution To make the problem easier, locate the coordinate system at the window's center, as shown in Figure 7.7.6. The depth at \(y\) feet or any subinterval rectangle is then $$ \text{Depth} = h(y) = 8-y.$$ The window's horizontal width is \(2x\) and the circle formula, \(x^{2}+y^{2}=1\), can be used to solve for \(x\) $$ \text{Length}=2x=2 \sqrt{1-y^{2}}=L(y) $$ Because \(y\) spans the interval \([-1,1]\) and 64 pounds per cubic foot is the weight-density for sea water, produces the pressure formula \(F\) $$ = w \int_{c}^{d} h(y)L(y)\: dy $$ $$= 64\: \int_{-1}^{1} (8-y)(2) \sqrt{1-y^{2}} \: dy .$$ Breaking the integral in two makes the solution simpler. $$F = 64 (16)\: \int_{-1}^{1} \sqrt{1-y^{2}} \: dy - 64(2) \int_{-1}^{1} y \sqrt{1-y^{2}} \: dy $$ The second integral is 0 because the integrand is odd and the integration limits are symmetric to the origin. Observing the first integral is a semicircle's area with radius 1 produces \(F\) $$ = 64(16)\frac{\pi}{2}-64(2)(0) $$ \( = 512 \pi \) \( \approx 1609.5 \) pounds. The fluid force on the window is about 1608.5 pounds.

Internal Links

Parent Article: Calculus II 07 Integration Applications