Calculus II 10.06 Polar Equations for Conics and Kepler's Laws

Previous	Calculus II 10.05 Area and Arc Length in Polar Coordinates
Next	Calculus III

10.6 Polar Equations for Conics and Kepler's Laws

• Analyze and write polar equations for conics
• Understand and use Kepler’s Laws for Planetary Motion

Polar Equations for Conics

Many important applications for conics use a foci as the reference point and not the origin for the coordinate system. For example, the sun lies at a foci on Earth’s orbit. Similarly, the light source for a parabolic reflector lies at its focus. This section describes polar equations for conics when one foci lies at the pole.

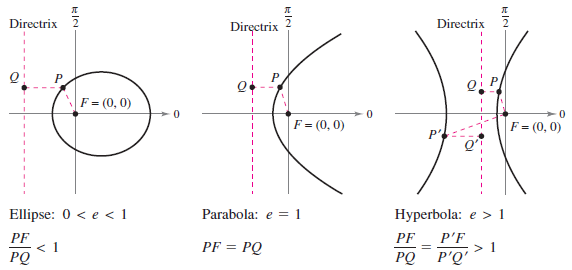
Theorem 10.6.1 Classifying Conics by Eccentricity

Section 10.1 described eccentricity for conics. Three different conics can be classified by their eccentricity.
Let \(F\) be a fixed point, focus, and let \(D\) be a fixed line, directrix, on a plane. Let \(P\) be another point on the plane and let \(e\), eccentricity, be the ratio for the distance between \(P\) and \(F\) to the distance between \(P\) and \(D\). The set for all points \(P\) with a given eccentricity is a conic.

1. The conic is an ellipse for \(0<e<1\).

2. The conic is a parabola for \(e=1\).

3. The conic is a hyperbola for \(e>1\).

As shown in Figure 10.6.1

Figure 10.6.1

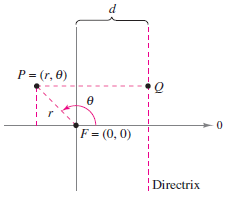
Theorem 10.6.2 Polar Equations for Conics

Figure 10.6.2

The graph for a polar equation with the form $$r=\frac{ed}{1 \pm e \cos \theta} \text{ or } r=\frac{ed}{1 \pm e \sin \theta} $$ is a conic, where \(e > 0\) is the eccentricity and \(|d|\) is the distance between the focus at the pole and its corresponding directrix. Proof This is a proof for \(r=ed/(1+e \cos \theta)\) with \(d>0\). Consider the focus \(F=(0,0)\) and a vertical directrix \(d\) units to the right, as shown in Figure 10.6.2. 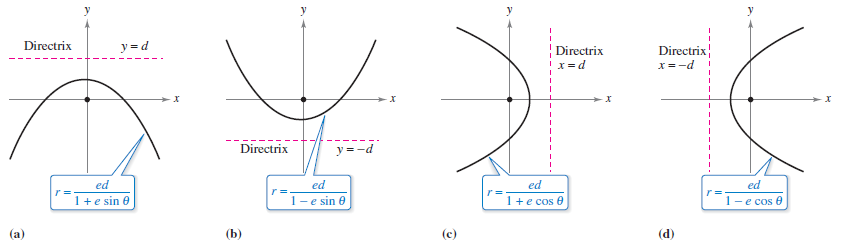If \(P=(r,\theta)\) is a point on the graph for \(r=ed/(1+e \cos \theta)\), then the distance between \(P\) and the directrix is $$PQ=|d-x|=|d-r \cos \theta|=\left|\frac{r(1+e \cos \theta)}{e}-r \cos \theta\right|=\left|\frac{r}{e}\right|$$ Because the distance between \(P\) and the pole is simply \(PF=|r|\), the \(PF\) to \(PQ\) ratio is $$\frac{PF}{PQ}=\left|\frac{r}{r/e}\right|=|e|=e$$ and, by Theorem 10.6.1, the graph must be a conic. The proof for the \(\sin\) case is similar. The four equations described are classified as follows, where \(d>0\). $$a.\:\text{ Horizontal directrix above the pole: } r=\frac{ed}{1 + e \sin \theta} $$ $$b.\:\text{ Horizontal directrix below the pole: } r=\frac{ed}{1 - e \sin \theta} $$ $$c.\:\text{ Vertical directrix to the right of the pole: } r=\frac{ed}{1 + e \cos \theta} $$ $$d.\:\text{ Vertical directrix to the left of the pole: }r=\frac{ed}{1 - e \cos \theta} $$ Figure 10.6.3 illustrates these four possibilities for a parabola. Note that for convenience, the equation for the directrix is shown in cartesian form.

The parabola as four polar equations.
Figure 10.6.3

Example 10.6.1 Determining a Conic from Its Equation

The graph for the conic is an ellipse where \(e=\frac{2}{3}\). Figure 10.6.4

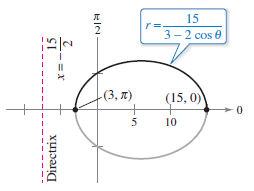
Sketch the graph for the conic $$r=\frac{15}{3-2 \cos \theta}$$ SolutionTo determine the conic type, rewrite the equation as $$r=\frac{5}{1-(2/3) \cos \theta}\:\:\:\:\color{red}{\text{Divide numerator and denominator by 3.}}$$ The graph for the conic is an ellipse where \(e=\frac{2}{3}\), as shown in Figure 10.6.3. The upper half is sketched by plotting points from \(\theta=0\) to \(\theta=\pi\). Using symmetry with respect to the polar axis, sketch the lower half.

For the ellipse in Figure 10.6.4, the major axis is horizontal and the vertices lie at \((15,0)\) and \((3,\pi)\). The major axis has length \(2a=18\). To find the length for the minor axis, use the equations \(e=c/a\) and \(b^{2}=a^{2}-c^{2}\) to conclude that

\(b^{2}=a^{2}-c^{2}=a^{2}-(ea)^{2}=a^{2}(1-e^{2}) \:\:\:\:\color{red}{\text{Ellipse}}\)

Plug in \(e=\frac{2}{3}\) produces

\(b^{2}=9^{2}[1-(2/3)^{2}]=45,\:b=\sqrt{45}=3\sqrt{5} \)

The minor axis is \(2b=6\sqrt{5}\). A similar analysis for hyperbolas yields

\(b^{2}=c^{2}-a^{2}=(ea)^{2}-a^{2}=a^{2}(e^{2}-1) \:\:\:\:\color{red}{\text{Hyperbola}}\)

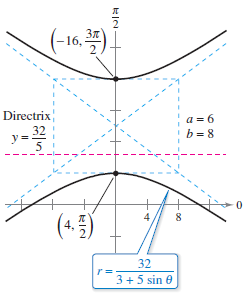
Example 10.6.2 Sketching a Conic from Its Polar Equation

The graph for the conic is a hyperbola where \(e=\frac{5}{3}\). Figure 10.6.5

Sketch the graph for the polar equation $$r=\frac{32}{3+5 \sin \theta}$$ Solution Dividing the numerator and denominator by 3 produces $$r=\frac{32/3}{1+(5/3) \sin \theta}$$ Because \(e=\frac{5}{3}>1\), the graph is a hyperbola. Because \(d=\frac{32}{5}\), the directrix is the line \(y=\frac{32}{5}\). The transverse axis for the hyperbola lies on the line \(\theta=\pi/2\), and the vertices are at $$(r,\theta)=\left(4,\frac{\pi}{2} \right) \text{ and } (r,\theta)=\left(-16,\frac{3\pi}{2} \right). $$ Because the transverse axis has length 12, then \(a=6\). Find \(b\) by plugging in the answers for \(a\) and \(e\). $$b^{2}= a^{2}(e^{2}-1)= 6^{2} \left[\left(\frac{5}{3}\right)^{2}-1\right]=64,\:b=\sqrt{64}=8 $$ The asymptotes for the hyperbola are determined by \(a\) and \(b\) as shown in Figure 10.6.5.

Kepler’s Laws[1]

Kepler’s Laws, named after the German astronomer Johannes Kepler[2], describe planetary orbits about the sun. This is the basis for modern Orbital Mechanics[3].

1. Each planet moves in an elliptical orbit with the sun as a focus.
2. A ray from the sun to the planet sweeps out equal areas from the ellipse in equal times.
3. The square of the period is proportional to the cube of the mean distance between the planet and the sun.

If Earth is used as a reference with one period being a year and one astronomical unit as the distance, then the proportionality constant is 1. For example, because Mars' mean distance to the sun \(D \approx 1.524\) AU, its period \(P\) is \(D^{3}=P^{2}\). Therefore, the period for Mars is \(P \approx 1.88\).

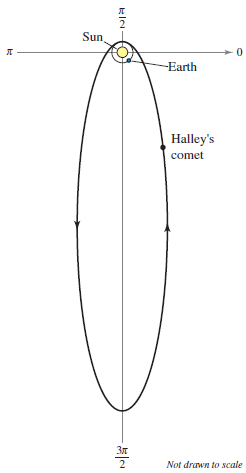
Kepler derived these laws empirically and Newton later validated them. Newton was able to show that each law can be deduced from universal laws for motion and gravitation that govern the movement for all heavenly bodies, including comets and satellites. Example 10.6.3 solves a problem for Edmund Halley's[4] comet.

Example 10.6.3 Halley's Comet[5]

Figure 10.6.6

Halley’s comet has an elliptical orbit with the sun at one focus and has an eccentricity where \(e \approx 0.967\). The length for the major axis is approximately 35.88 astronomical units (AU). An astronomical unit is defined as the mean distance between Earth and the sun, 93 million miles. a. Find a polar equation for the orbit. b. How close does Halley’s comet come to the sun? Solution Using a vertical axis choose the form $$r=\frac{ed}{1 + e \sin \theta} $$ Because the vertices for the ellipse occur when \(\theta=\pi/2\) and \(\theta=3\pi/2\), the length for the major axis is the sum for the \(r\)-value vertices, shown in Figure 10.6.6. \(2a\) $$= \frac{0.967d}{1+0.967} + \frac{0.967d}{1-0.967} $$ 35.88 \(\approx 29.79d.\) \(\:\:\:\:\color{red}{ 2a \approx 35.88} \) \(d\) \(\approx 1.204\) \(ed\) \(\approx (0.967)(1.204) \approx 1.164\) Using this value in the equation produces $$r=\frac{1.164}{1 + 0.967 \sin \theta} \text{ Answer for } a.$$ where \(r\) is measured in AU. To find the closest approach to the sun is \(c=ea \approx (0.967)(17.94) \approx 17.35\) Because \(c\) is the distance between the focus and the center, the closest point is \(a-c\) \( \approx 17.94-17.35\) \( \approx 0.59 \)AU \( \approx 55,000,000 \) miles. Answer for b.

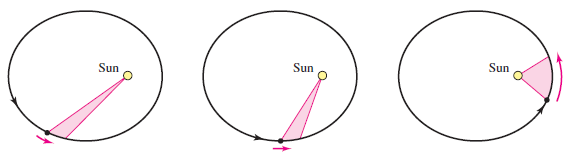
Kepler’s Second Law states that as a planet moves about the sun, a ray from the sun to the planet sweeps out equal areas in equal times. This law can also be applied to comets or asteroids with elliptical orbits. For example, Figure 10.6.7 shows the orbit for the asteroid Apollo about the sun. Applying Kepler’s Second Law to this asteroid, the closer it is to the sun, the greater its velocity, because a short ray must be moving quickly to sweep out as much area as a long ray.

A ray from the sun to the asteroid Apollo sweeps out equal areas in equal times.
Figure 10.6.7

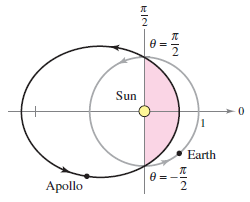
Example 10.6.4 The Asteroid Apollo

Figure 10.6.8

The asteroid Apollo has a period equal to 661 Earth days. Its orbit is approximated by the ellipse $$ r= \frac{1}{1+(5/9)\cos \theta}=\frac{9}{9+5\cos \theta}$$ where \(r\) is measured in AUs. How long does it take Apollo to move from the position \(\theta=-\pi/2\) to \(\theta=\pi/2\), as shown in Figure 10.6.8? Solution Begin by finding the area swept out as \(\theta\) in creases from \(-\pi/2\) to \(\pi/2\). $$A=\frac{1}{2} \int_{-\pi/2}^{\pi/2} \left( \frac{9}{9+5\cos \theta} \right)^{2} \:\:\:\:\color{red}{\text{Area for a polar graph}}$$ Substitute \(u=\tan(\theta/2)\), as discussed in Section 8.6, produces $$A=\frac{81}{112} \left[ \frac{-5 \sin \theta}{9+5\cos \theta} + \frac{18}{\sqrt{56}} \arctan \frac{\sqrt{56}\tan(\theta/2)}{14} \right]_{-\pi/2}^{\pi/2} \approx 0.90429.$$ Because the major axis has length \(2a=81/28\) and the eccentricity is \(e=5/9\), \(b\) equals $$b=a\sqrt{1-e^{2}}=\frac{9}{\sqrt{56}}. $$ The area for the ellipse is $$Area for ellipse= \pi ab= \pi \left(\frac{81}{56}\right)\left(\frac{9}{\sqrt{56}}\right) \approx 5.46507. $$ Apply Kepler’s Second Law and the 661 day orbital period, to conclude that the time \(t\) required is $$ \frac{t}{661} = \frac{\text{Area for elliptical segment}}{\text{Area for ellipse}} \approx \frac{0.90429}{5.46507} $$ which reduces to \(t \approx 109\) days.

Internal Links

Parent Article: Calculus II 10 Conics Parametric Equations and Polar Coordinates