Calculus II 10.05 Area and Arc Length in Polar Coordinates

Previous	Calculus II 10.04 Polar Coordinates and Polar Graphs
Next	Calculus II 10.06 Polar Equations for Conics and Kepler's Laws

10.5 Area and Arc Length in Polar Coordinates

• Find the area for a region bounded by a polar graph.
• Find the intersection points between two polar graphs.
• Find the arc length for a polar graph.
• Find the area for a rotated surface in polar form.

Area for a Polar Region

The area for a circle section is \(A=1/2\theta r^{2}\). Figure 10.5.1 Figure 10.5.2

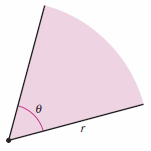
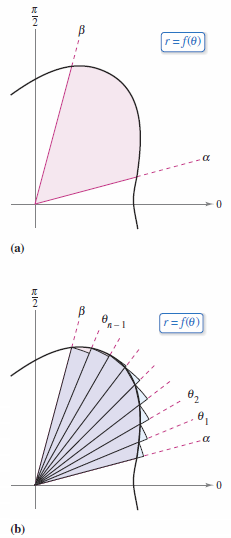
Calculating the area for a polar region parallels that for a rectangular region but uses circle sectors, pie slices, rather than rectangles, brownie slices. Try comparing the area between a Neapolitan Pizza[1] and a Sicilian Pizza[2]. The area for a circle sector with radius \(r=1/2 \theta r^{2}\) measured in radians, is shown in Figure 10.5.1. Consider the function \(r=f(\theta)\), where \(f\) is continuous and nonnegative on the interval \(\alpha \leqslant \theta \leqslant \beta \). The region bounded by the graph for \(f\) and the radial lines \(\theta=\alpha\) and \(\theta = \beta\) is shown in Figure 10.5.2(a). To find the area for this region partition the interval \([\alpha,\beta]\) into \(n\) equal subintervals \(\alpha = \theta_{0} < \theta_{1} < \theta_{2} < \cdots < \theta_{n-1} < \theta_{n} = \beta\). Then approximate the area by summing the area for each sector, as shown in Figure 10.5.2(b). Radius for the \(i\)th sector \(= f(\theta_{i})\) Central angle for the \(i\)th sector $$= \frac{\beta - \alpha}{n} = \Delta \theta $$ \(A\) $$\approx \sum_{i=1}^{n} \left( \frac{1}{2} \right ) \Delta \theta [f(\theta)_{i}]^{2}$$ Taking the limit as \(n \to \infty\) produces \(A\) $$= \lim_{n \to \infty} \frac{1}{2} \sum_{i=1}^{n} [f(\theta)_{i}]^{2} \Delta \theta$$ $$= \frac{1}{2} \int_{\alpha}^{\beta} [f(\theta)]^{2} \:d\theta$$ Which leads to Theorem 10.5.1.

Theorem 10.5.1 Area in Polar Coordinates

If \(f\) is continuous and nonnegative over the interval \([\alpha, \beta]\), \(0 < \beta - \alpha \leqslant 2 \pi\), then the area for the region bounded by the graph for \(r=f(\theta)\) between the radial lines \(\theta=\alpha\) and \(\theta = \beta\) is

\(A\)	$$= \frac{1}{2} \int_{\alpha}^{\beta} [f(\theta)]^{2} \:d \theta$$
	$$= \frac{1}{2} \int_{\alpha}^{\beta} r^{2} \:d\theta$$	\(\:\:\:\: \color{red}{0 < \beta - \alpha \leqslant 2 \pi} \)

This works on a continuous nonpositive function. The formula is not necessarily valid, however, when \(f\) takes on both positive and negative values on the interval \([\alpha, \beta]\).

Example 10.5.1 Finding the Area for a Polar Region

The area for one petal on the rose curve between the radial lines \(\theta=-\pi/6\) and \(\theta=\pi/6\) is \(3\pi/4\). Figure 10.5.3

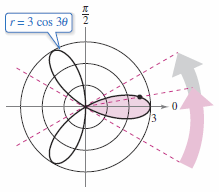
Find the area for one petal on the rose curve \(r=3 \cos 3 \theta\). Solution In Figure 10.5.3 the petal on the right is traced as \(\theta\) increases from \(\theta=-\pi/6\) to \(\theta=\pi/6\). The area is $$A= \frac{1}{2} \int_{\alpha}^{\beta} r^{2} \:d\theta $$ $$= \frac{1}{2} \int_{-\pi/6}^{\pi/6} (3 \cos 3 \theta)^{2} \:d\theta $$     Area in polar coordinates. $$= \frac{9}{2} \int_{-\pi/6}^{\pi/6} \frac{1+ \cos 6 \theta}{2} \:d\theta $$     Power-reducing formula $$= \frac{9}{4} \left[ \theta + \frac{\sin 6 \theta}{6} \right]_{-\pi/6}^{\pi/6}$$ $$= \frac{9}{4} \left( \frac{\pi}{6} + \frac{\pi}{6} \right) = \frac{3\pi}{4}$$ Integrating between 0 and \(2\pi\) will not produce the area for all three petals. The result is \(9\pi/2\), twice the actual area. The duplication occurs because the rose curve is traced twice as \(\theta\) increases from 0 to \(2 \pi\).

Example 10.5.2 Finding the Area Bounded by a Single Curve on a Limaçon[3]

The area between the inner and outer loops is approximately 8.34. Figure 10.5.4

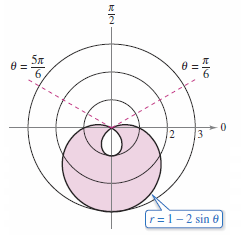
Find the area for the region lying between the limaçon's inner and outer loops. The limaçon's formula is \(r=1-2 \sin \theta\). Solution In Figure 10.5.4 notice the inner loop is traced as \(\theta\) increases from \(\pi/6\) to \(5\pi/6\). The area for the inner loop is \(A_{1}\) $$= \frac{1}{2} \int_{\pi/6}^{5\pi/6} (1 - 2 \sin \theta)^{2} \:d\theta $$     Area in polar coordinates. $$= \frac{1}{2} \int_{\pi/6}^{5\pi/6} (1 - 4 \sin \theta + 4 \sin^{2} \theta) \:d\theta $$ $$= \frac{1}{2} \int_{\pi/6}^{5\pi/6} \left[ 1 - 4 \sin \theta + 4 \left (\frac{1- \cos 2 \theta}{2}\right) \right] \:d\theta $$     Power-reducing formula $$= \frac{1}{2} \int_{\pi/6}^{5\pi/6} (3- 4 \sin \theta - 2 \cos 2 \theta) \:d\theta $$     Simplify $$= \frac{1}{2} \Bigg[ 3\theta + 4 \cos \theta - \sin 2 \theta \Bigg]_{\pi/6}^{5\pi/6} $$ $$= \frac{1}{2} ( 2\pi - 3 \sqrt{3}) = \pi - \frac{3 \sqrt{3}}{2}$$ In a similar way \(\theta\) can be integrated from \(5\pi/6\) to \(13\pi/6\) to find the area for the outer loop is \(A_{2}=2\pi+(3 \sqrt{3}/2)\). The are between the loops is the difference between \(A_{2}\) and \(A_{1}\). $$A=A_{2} - A_{1} = \left( 2\pi + \frac{3 \sqrt{3}}{2} \right) - \left( \pi - \frac{3 \sqrt{3}}{2} \right) = \pi + 3 \sqrt{3} \approx 8.34$$

Intersection Points between Two Polar Graphs

Three intersecting points: \((1,\pi/2)\), \((-1,0)\), and \((1,3\pi/2)\). Figure 10.5.5 Satellite orbits can cross without causing a collision. Figure 10.5.6

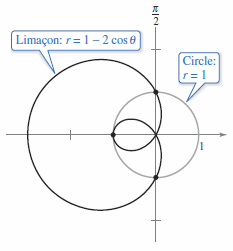
Because a point may be represented in different ways in polar coordinates, care must be taken in determining the intersecting points between two polar graphs. For example, consider the intersecting points between the graphs for \(r=1-2 \cos \theta \text{ and } r=1\) as shown in Figure 10.5.5. Finding intersecting points in cartesian equations is done by solving an equation system simultaneously. \(r\) \(=1-2 \cos \theta\)     First equation \(\color{red}{1}\) \(=1-2 \cos \theta\)     Substitute \(r=1\) from 2nd equation into 1st equation. \(\cos \theta\) \(=0\)     Simplify \( \theta\) $$=\frac{\pi}{2}, \:\frac{3\pi}{2} $$     Solve for \(\theta\) The corresponding intersecting points are \((1,\pi/2)\) and \((1,3\pi/2)\). Figure 10.5.5 shows a third intersection point. Thus, always remember to sketch the graph. The third point was not found because it has different coordinates in both graphs. Table 10.5.1 Graph Point \(r=1\) \((1,\pi)\) \(r=1-2 \cos \theta\) \((-1,0)\) An additional complication is the pole is represented by \((0,\theta)\) where \(\theta\) is any angle. Check for agreement a between the poles for the graphs. A similar problem is finding collision points with two satellites in intersecting orbits about the Earth, as shown in Figure 10.5.6. The satellites will not collide as long as they reach the intersecting points at different times, \(\theta\) values. Collisions will occur only at simultaneous points --those that are reached at the same time, \(\theta\) values.

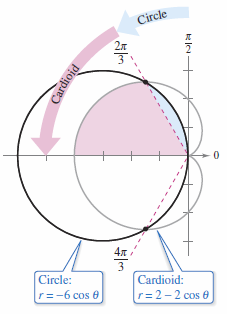
Example 10.5.3 Finding the Area Between a Cardioid and a Circle

Figure 10.5.7

Find the area common to these curves. \(r=-6 \cos \theta \)     \( \color{red}{\text{Circle}} \) \(r=2-2 \cos \theta \)     \( \color{red}{\text{Cardioid}} \) Solution Because both curves are symmetric with respect to the \(x\)-axis calculate for the upper half-plane, as shown in Figure 10.5.7. The blue shaded region lies between the circle and the radial line \(\theta = 2\pi/3\). Because the circle has coordinates \((0,\pi/2)\) at the pole, integration between \(\pi/2\) and \(2\pi/3\) will yield the area. The red shaded region lies between the cardioid and the radial lines \(\theta=2\pi/3\) and \(\theta=\pi\). Find this area by integrating between \(2\pi/3\) and \(\pi\). Add both integrals to find the common area lying above the radial line \(\theta=\pi\). Then multiply by 2 to find the total area. Blue Region Red Region $$\frac{1}{2} A $$ $$= \frac{1}{2} \int_{\pi/2}^{2\pi/3}(-6 \cos \theta)^{2}\:d\theta $$ $$+ \frac{1}{2} \int_{2\pi/3}^{\pi}(2-2 \cos \theta)^{2}\:d\theta$$ $$= 18 \int_{\pi/2}^{2\pi/3} \cos^{2} \theta\:d\theta $$ $$+ \frac{1}{2} \int_{2\pi/3}^{\pi}(4-8 \cos \theta + 4 \cos^{2} \theta)\:d\theta$$ $$= 9 \int_{\pi/2}^{2\pi/3} (1+ \cos 2 \theta)\:d\theta $$ $$+ \int_{2\pi/3}^{\pi}(3-4 \cos \theta + 2 \cos^{2} \theta)\:d\theta$$ $$= 9 \left[ \theta + \frac{\sin 2 \theta}{2} \right]_{\pi/2}^{2\pi/3} $$ $$+ \left[ 3\theta-4 \sin \theta +\frac{\sin 2 \theta}{2} \right]_{2\pi/3}^{\pi}$$ $$= 9 \left( \frac{2\pi}{3} - \frac{\sqrt{3}}{4} - \frac{\pi}{2} \right) $$ $$+ \left( 3\pi-2\pi+2\sqrt{3}+ \frac{\sqrt{3}}{4} \right)= \frac{5\pi}{2}$$ Multiplying by 2 produces \(5\pi \approx 15.7\).

Arc Length in Polar Form

The formula for a polar arc's length can be obtained from the arc length formula for a curve described by parametric equations as described in Theorem 10.5.2.

Theorem 10.5.2 Arc Length for a Polar Curve

Let \(f\) be a function whose derivative is continuous on an interval \(\alpha \leqslant \theta \leqslant \beta \). Let \(r=f(\theta)\) be a parametric equation from \(\theta=\alpha\) to \(\theta=\beta\). The length for the graph is

$$S= \int_{\alpha}^{\beta} \sqrt{ [f(\theta)]^{2} + [f{}^{\prime}(\theta)]^{2}}\:d\theta=\int_{\alpha}^{\beta} \sqrt{r^{2}+ \left(\frac{dr}{d\theta} \right)^{2} } \:d\theta$$

Example 10.5.4 Finding the Length for a Polar Curve

Figure 10.5.8

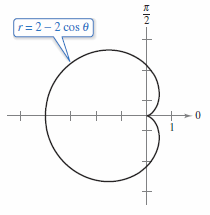
Find the arc length from \(\theta=0\) to \(\theta=2\pi\) for the cardioid \(r=f(\theta)=2 - 2 \cos \theta\) as shown in Figure 10.5.8. Solution Because \(f{}^{\prime}(\theta)=2 \sin \theta\), the arc length can be found as follows. $$S$$ $$= \int_{0}^{2\pi} \sqrt{ (2 - 2 \cos \theta)^{2} + (2 \sin \theta)^{2}}\:d\theta $$     Insert values into Theorem 10.5.2 $$=2\sqrt{2} \int_{0}^{2\pi} \sqrt{1-\cos \theta }\:d\theta $$     Simplify $$=2\sqrt{2} \int_{0}^{2\pi} \sqrt{ 2 \sin^{2} \frac{\theta}{2} }\:d\theta $$     Trigonometric identity $$=4 \int_{0}^{2\pi} \sin \frac{\theta}{2} \:d\theta $$     \( \color{red}{\sin \frac{\theta}{2} \geqslant 0 \text{ for } 0 \leqslant \theta \leqslant 2 \pi} \) $$=8 \left[ - \cos \frac{\theta}{2} \right]_{0}^{2\pi} $$ $$=8 (1+1) = 16$$

Area for a Rotated Surface

The polar coordinate formula for a rotated surface are are drawn from the parametric versions given in Theorem 10.3.3, using the equations \(x=r \cos \theta\) and \(y= r \sin \theta\) and described in Theorem 10.5.3.

Theorem 10.5.3 Area for a Rotated Surface in Polar Form

Let \(f\) be a function whose derivative is continuous on an interval \(\alpha \leqslant \theta \leqslant \beta \). The area for a rotated surface formed by revolving the graph \(r=f(\theta)\) from \(\theta=\alpha\) to \(\theta=\beta\) about a line is: $$1.\:S=2\pi \int_{\alpha}^{\beta} f(\theta) \sin \theta \sqrt{ [f(\theta)]^{2} + [f{}^{\prime}(\theta)]^{2}}\:d\theta \:\:\:\: \color{red}{ \text{ About the polar axis}}$$ $$2.\:S=2\pi \int_{\alpha}^{\beta} f(\theta) \cos \theta \sqrt{ [f(\theta)]^{2} + [f{}^{\prime}(\theta)]^{2}}\:d\theta \:\:\:\: \color{red}{ \text{About the line }\theta=\frac{\pi}{2} }$$

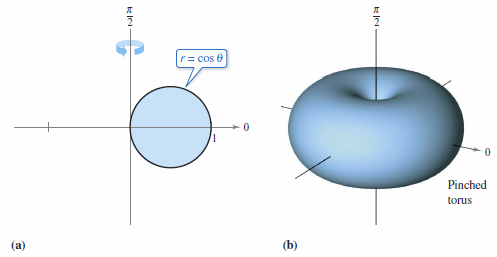
Example 10.5.5 Finding the Area for a Rotated Surface

Find the area for the rotated surface formed by revolving the circle, \(r=f(\theta)= \cos \theta\), about the line \(\theta=\pi/2\), as shown in Figure 10.5.9.

Figure 10.5.9

Solution Use the second formula in Theorem 10.5.3 with \(f{}^{\prime}(\theta)=-\sin \theta\). Tracing the circle as \(\theta\) increases from 0 to \(\pi\) produces

$$S$$	$$=2\pi \int_{0}^{\pi} \cos \theta (\cos \theta) \sqrt{ \cos^{2} \theta + \sin^{2} \theta }\:d\theta $$	Insert values into Theorem 10.5.3
	$$=2\pi \int_{0}^{\pi} \cos^{2} \theta \:d\theta $$	Trigonometric identity
	$$=\pi \int_{0}^{\pi} (1+\cos 2 \theta) \:d\theta $$	Trigonometric identity
	$$=\pi \left[ \theta + \frac{\sin \theta}{2} \right]_{0}^{\pi} = \pi^{2}$$

Internal Links

Parent Article: Calculus II 10 Conics Parametric Equations and Polar Coordinates