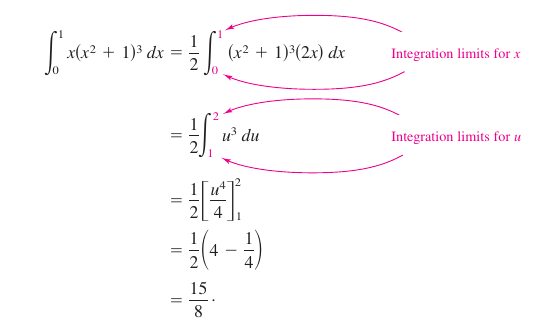Calculus I 04.05 Integration by Substitution

Previous	Calculus I 04.04 The Fundamental Theorem of Calculus
Next	Calculus I 04.06 Numerical Integration

4.5 Integration by Substitution

• Change variables to find an indefinite integral.
• Change variables to evaluate a definite integral.
• Evaluate a definite integral involving an even or odd function.
• Use pattern recognition to find an indefinite integral.
• Use the General Power Rule for Integration to find an indefinite integral.

Pattern Recognition

Calculus provides techniques for integrating composite functions. The discussion is split into two parts, pattern recognition and variables changes. Both techniques involve a \(u\)-substitution.

Substitution in integration is comparable to the Chain Rule in differentiation. Consider the differentiable functions

\(y=F(u)\:\:\:\;\text{and}\:\:\:\:u=g(x)\)

the Chain Rule states that

$$\frac{d}{dx}[F(g(x))]={F}'(g(x)){g}'(x).$$

From the antiderivatives definition, it follows that,

$$\int {F}'(g(x)){g}'(x)\:dx=F(g(x))+C.$$

The results are summarized in Theorem 4.5.1.

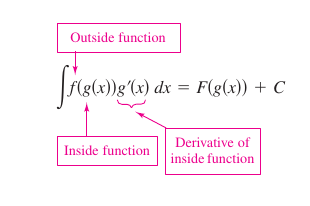
Theorem 4.5.1 Composite Function Antidifferentiation

Let \(g\) be a function whose range is an interval \(I\). Let \(f\) be a function that is continuous on \(I\). If \(g\) is differentiable on its domain and \(F\) is an antiderivative for \(f\) on \(I\), then

$$\int f(g(x)){g}'(x)\:dx=F(g(x))+C.$$

Letting \(u=g(x)\: \text{gives} \: du={g}'(x)\:dx\) and

$$\int f(u)\: du=F(u)+C.$$

Distinguishing between \(f(g(x))\) and \({g}'(x)\) is presented later in the discussion.

Examples 4.5.1 and 4.5.2 show how to apply Theorem 4.5.1 directly by recognizing \(f(g(x))\) and \({g}'(x)\). Note the composite function in the integrand has an outside function \(f\) and an inside function \(g\). The derivative \({g}'(x)\) is present as a factor in the integrand.

Example 4.5.1 Recognizing the \(f(g(x){g}'(x)\) Pattern in a Polynomial

Find

$$\int (x^2+1)^2(2x)\:dx.$$

Solution Letting \(g(x)=x^2+1\) produces

\({g}'(x)=2x\)

and

\(f(g(x)){g}'(x)\)=f(x^2+1)=(x^2+1)^2.\)

From this recognize the integrand follows the \(f(g(x)){g}'(x)\) pattern. Using the Power Rule from Theorem 4.5.1 the expression can be rewritten as

$$\int {\color{red}{\overbrace{\color{black}{(x^2+1)}}^{\color{red}{\text{f(g(x))}}}}}{\color{red}{\overbrace{\color{black}{(2x)}}^{\color{red}{\text{g}'(x)}}}}\:dx=\frac{1}{3}(x^2+1)^3+C.$$

Use the Chain Rule to check that the derivative above is the integrand for the original integral.

Example 4.5.2 Recognizing the \(f(g(x)){g}'(x)\) Pattern in a Trigonometric

Find

$$\int 5 \cos 5x\:dx.$$

Solution Letting \(g(x)=5x\) produces

\({g}'(x)=5\)

and

\(f(g(x)){g}'(x)=f(5x)=\cos 5x\).

From this recognize the integrand follows the \(f(g(x)){g}'(x)\) pattern. Using the Cosine Rule for Integration and Theorem 4.5.1 the expression can be rewritten as

$$\int {\color{red}{\overbrace{\color{black}{(\cos 5x)}}^{\color{red}{\text{f(g(x))}}}}}{\color{red}{\overbrace{\color{black}{(5)}}^{\color{red}{\text{{g}'(x)}}}}}\:dx=\frac{1}{3}(x^2+1)^3+C.$$

Check this by differentiating \(\sin 5x+C\) to produce the original integrand.

The integrands in Examples 4.5.1 and 4.5.2 fit the \(f(g(x)){g}'(x)\) pattern exactly. Recognition was obvious. Extend this technique considerably with the Constant Multiple Rule

$$\int kf(x)\:dx=k\int f(x)\:dx.$$

Many integrands contain the essential part, the variable part, for \({g}'(x)\) but are missing a constant multiple. Multiply and divide by the necessary constant multiple, as shown in Example 4.5.3 below.

Example 4.5.3 Multiplying and Dividing by a Constant

Find the indefinite integrand

$$\int \:x(x^2+1)^2 \:dx$$

Solution While similar to Example 4.5.1 the integrand is missing the factor 2. Recognizing that \(2x\) is the derivative for \(x^2+1\), let

\(g(x)=x^2+1\)

and supply the \(2x\) as.

$$\int \:x(x^2+1)^2 \:dx$$	$$=\int \:x(x^2+1)^2 \left ( \frac{1}{2} \right ) (2x)\:dx$$	Multiply and divide by 2
	$$=\frac{1}{2} \int {\color{red}{\overbrace{\color{black}{(x^2+1)}}^{\color{red}{\text{f(g(x))}}}}} {\color{red}{\overbrace{\color{black}{(2x)}}^{\color{red}{\text{{g}'(x)}}}}}\:dx$$	Constant Multiple Rule
	$$=\frac{1}{2} \left [ \frac{(x^2+1)^3}{3} \right ]+C$$	Integrate
	$$=\frac{1}{6}(x^2+1)^3+C$$	Simplify

In practice, most people would not write as many steps as in Example 4.5.3. For example, the integrand could be evaluated by simply writing

$$\int x(x^2+1)^2 \:dx$$	$$=\frac{1}{2} \int (x^2+1)^2(2x)\:dx$$
	$$=\frac{1}{2} \left [ \frac{(x^2+1)^3}{3} \right ] + C$$
	$$=\frac{1}{6}(x^2+1)^3+C$$

Be sure the Constant Multiple Rule applies only to constants. Multiplying and dividing by a variable and then moving it outside the integral sign invalidates it, so don't do it. For example,

$$\int x(x^2+1)^2 \:dx \ne \frac{1}{2} \int (x^2+1)^2(2x)\:dx.$$

If it were legitimate to move variable quantities outside the integral sign, entire integrand could be moved out and simplify the whole process. But the result is incorrect.

Change Variables

With a formal change variables, completely rewrite the integral in \(u\) and \(du\) terms or any other variable. Although this procedure can involve more written steps than the pattern recognition illustrated in Examples 4.5.1 to 4.5.3, it is useful for complicated integrands. The change variables technique uses Leibniz notation for the differential. That is, if \(u=g(x)\), then \(du={g}'(x)\:dx\), and the integral in Theorem 4.5.1 takes the form

$$\int f(g(x)){g}'(x)\:dx= \int f(u)\:du=F(u)+C.$$

Example 4.5.4 Change Variables

Find

$$\int \sqrt{2x-1} \:dx.$$

Solution Let \(u\) be the inner function, \(u=2x-1\). Then calculate the differential \(du\) to be \(du=2\:dx\). Using \(\sqrt{2x-1}=\sqrt{u}\) and \(dx=du/2\), substitute to produce

$$\int \sqrt{2x-1} \:dx$$	$$=\int \sqrt{u} \left ( \frac{du}{2} \right )$$	Integral in \(u\) terms
	$$=\frac{1}{2} \int u^{1/2}\:du$$	Constant Multiple Rule
	$$=\frac{1}{2} \left ( \frac{u^{3/2}}{3/2} \right ) +C$$	Antiderivative in \(u\) terms
	$$=\frac{1}{3} u^{3/2}+C$$	Simplify
	$$=\frac{1}{3}(2x-1)^{3/2}+C$$	Antiderivatives in \(x\) terms

Because integration is usually more difficult than differentiation, always check the answer to an integration problem by differentiating. Consider Example 4.5.4, differentiate \(\frac{1}{3} (2x-1)^{3/2}+C\) to verify the original integrand.

Example 4.5.5 Change Variables

Find

$$\int x\sqrt{2x-1} \:dx.$$

Solution Let \(u\) be the inner function, \(u=2x-1\) and obtain \(dx=du/2\). Because the integrand contains an \(x\) factor, solve for \(x\) in \(u\) terms.

$$u=2x-1 \rightarrow x=\frac{u+1}{2}$$

Solve for \(x\) in \(u\) terms

Use substitution to produce

$$\int x\sqrt{2x-1} \:dx$$	$$=\int \left ( \frac{u+1}{2} \right ) u^{1/2} \left ( \frac{du}{2} \right )$$
	$$=\frac{1}{4} \int (u^{3/2}+ u^{1}{2})\:du$$
	$$=\frac{1}{4} \left ( \frac{u^{5/2}}{5/2}+ \frac{u^{3/2}}{3/2} \right ) +C$$
	$$=\frac{1}{10} (2x-1)^{5/2}+\frac{1}{6}(2x-1)^{3/2}+C.$$

Example 4.5.5 solved for \(x\) in \(u\) terms to complete the change variables. Sometimes this is very difficult. Fortunately, it is not always necessary, as shown Example 4.5.6.

Example 4.5.6 Change Variables Trigonometry

Find

$$ \int \sin^2 3x \cos 3x\: dx.$$

Solution Because \(\sin^2 3x= (\sin 3x)^2\), let \(u=\sin 3x\). Then

\(du = (\cos 3x)(3)\:dx.\)

Because \(\cos 3x \:dx\) is in the original integral, rewrite the expression as

$$\frac{du}{3}=\cos 3x\:dx$$

Substituting \(u\) and \(du/3\) in the original integral yields

$$ \int \sin^2 3x \cos 3x\: dx$$	$$=\int u^2 \frac{du}{3}$$
	$$=\frac{1}{3} \int u^2 \:du$$
	$$=\frac{1}{3} \left ( \frac{u^3}{3} \right )+C$$
	$$=\frac{1}{9} \sin^3 3x +C.$$

Verify by differentiating

$$\frac{d}{dx} \left [ \frac{1}{9}\sin^3 3x +C \right ]$$	$$= \left (\frac{1}{9} \right )(3)(\sin 3x)^2(\cos 3x)(3)$$
	\(=\int \sin^2 3x \cos 3x\)

Because differentiation produces the original integrand the answer is verified.

Guidelines for Making a Change Variables

1. Choose a substitution \(u=g(x)\). Usually, it is best to choose the inner part from a composite function, such as a quantity raised to a power.
2. Compute \(du={g}'(x)\:dx\).
3. Rewrite the integral in \(u\)terms.
4. Find the resulting integral in \(u\) terms.
5. Replace \(u\) by \(g(x)\) to obtain an antiderivative in \(x\) terms.
6. Check the answers by differentiating.
So far, two techniques for applying substitution were discussed. There are more techniques and each differs slightly from the others. Remember the goal is the same with each technique, trying to find an antiderivative for the integrand.

The General Power Rule for Integration

A common \(u\)-substitutions is quantities in the integrand raised to a power. Because this substitution is so important, it has a special name, the General Power Rule for Integration. The proof for this rule follows directly from the, simpler, Power Rule for Integration, together with Theorem 4.5.1.

Theorem 4.5.2 The General Power Rule for Integration

If \(g\) is a differentiable function for \(x\), then

$$\int [g(x)]^n{g}'(x)\:dx=\frac{[g(x)]^{n+1}}{n+1}+C,\:\:\:\: n \neq -1.$$

Equivalently, if \(u=g(x)\), then

$$\int u^n \:du=\frac{ u^{n+1}}{n+1}+C,\:\:\:\:n \neq -1.$$

Example 4.5.7 Substitution and the General Power Rule

Some integrals whose integrands involve quantities raised to powers cannot be found by the General Power Rule. Consider the two integrals

$$\int x(x^2+1)^2\:dx\:\:\:\:\text{and}\:\:\:\:\int (x^2+1)^2\:dx.$$

The substitution

\(u=x^2+1\)

works in the first integral, but not in the second. In the second, the substitution fails because the integrand lacks the factor \(x\) needed for \(du\). Fortunately, for this particular integral, expand the integrand as

\((x^2+1)^2=x^4+2x^2+1\)

and use the Power Rule to integrate each term.

Change Variables for Definite Integrals

When using \(u\)-substitution with a definite integral, it is often convenient to determine the integration limits for \(u\) than to convert the antiderivative back to \(x\) and evaluate at the original limits. This change variables is stated explicitly in the Theorem 4.5.3. The proof follows from Theorem 4.5.1 combined with the Fundamental Theorem of Calculus.

Theorem 4.5.3 Change Variables

If the function \(u=g(x)\) has a continuous derivative on the closed interval \([a,b]\) and \(f\) is continuous on the range for \(g\), then

$$ \int_{a}^{b} f(g(x)){g}'(x)\:dx=\int_{g(a)}^{g(b)} f(u)\: du.$$

Example 4.5.8 Change Variables with Limits

Evaluate

$$\int_{0}^{1} x(x^2+1)^3\:dx.$$

Solution Let \(u=x^2+1\). This produces

\(u=x^2+1\:\:\rightarrow \:\: du=2x\:dx.\)

Before substituting, determine the new upper and lower integration limits.

Lower Limit	Upper Limit
When \(x=0,\:u=\color{red}{0}^2+1=1.\)	When \(x=1,\:u=\color{red}{1}^2+1=2.\)

Substitute to obtain

Notice the same result occurs when you rewrite the antiderivative \(\frac{1}{2}(u^4/4)\) in \(x\) terms evaluate the definite integral at the original integration limits, as shown below.

$$\frac{1}{2} \left [ \frac{u^4}{4} \right ]_{1}^{2}$$	$$=\frac{1}{2} \left [ \frac{(x^2+1)^4}{4} \right ]_{0}^{1}$$
	$$=\frac{1}{2} \left ( 4-\frac{1}{4} \right )$$
	$$=\frac{15}{8}.$$

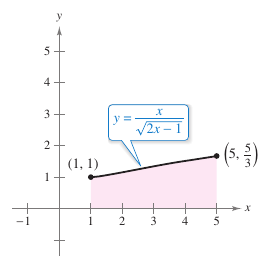
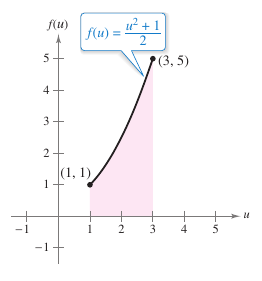
Example 4.5.9 Change Variables with Quotient

Evaluate the definite integral,

$$\int_{1}^{5} \frac{x}{\sqrt{2x-1}}\:dx$$

Solution Let \(u=\sqrt{2x-1}\). Then differentiate.

\(u^2\)	\(=2x-1\)
\(u^2+1\)	\(=2x\)
$$\frac{u^2+1}{2}$$	\(=x\)
\(u\:du\)	\(=dx\)	Differentiate each side.

Before substituting, determine the new upper and lower integration limits.

Lower Limit	Upper Limit
When \(x=1\), \(u=\sqrt{2-1}=1.\)	When \(x=5\), \(u=\sqrt{10-1}=3.\)

Substitute into the original.

$$\int_{1}^{5} \frac{x}{\sqrt{2x-1}}\:dx$$	$$=\int_{1}^{3} \frac{1}{u} \left ( \frac{u^2+1}{2} \right )u\:du$$
	$$=\frac{1}{2} \int_{1}^{3} ( u^2+1)\:du$$
	$$=\frac{1}{2} \left [ \frac{u^3}{3}+u \right ]_{1}^{3}$$
	$$=\frac{1}{2} \left ( 9+3-\frac{1}{3} - 1 \right )$$
	$$=\frac{16}{3}.$$

The area for the region before substitution is \(16/3\) Figure 4.5.1 The area for the region after substitution is \(16/3\) Figure 4.5.2

A geometric interpretation for the equation $$\int_{1}^{5} \frac{x}{\sqrt{2x-1}}\:dx=\int_{1}^{3} \frac{u^2+1}{2} \:du$$ reveals the two different regions in Figures 4.5.1 and 4.5.2 have the same area. When evaluating definite integrals by substitution, it is possible for the upper integration limit for the \(u\)-variable to be smaller that the lower limit. When this happens, do not rearrange the limits. Simply evaluate as usual. For example, after substituting \(u=\sqrt{1-x}\) in the integral $$ \int_{0}^{1} x^2(1-x)^{1/2}\: dx$$ produces \(u=\sqrt{1-\color{red}{1}}=0\) when \(x=1\), and \(u=\sqrt{1-\color{red}{0}}=1\) when \(x=0\). The correct \(u\)-variable form for this integral is $$ -2 \int_{1}^{0} (1-u^2)^{2} u^2 \: du.$$ Evaluate the integrand by expanding as shown below. $$ -2 \int_{1}^{0} (1-u^2)^{2} u^2 \: du = -2 \left [ \frac{u^3}{3}-\frac{2u^5}{5}+\frac{u^7}{7} \right ]_{1}^{0}= -2 \left ( -\frac{1}{3}+\frac{2}{5}-\frac{1}{7} \right ) = \frac{16}{105}$$

Integrating Even and Odd Functions

Figure 4.5.3

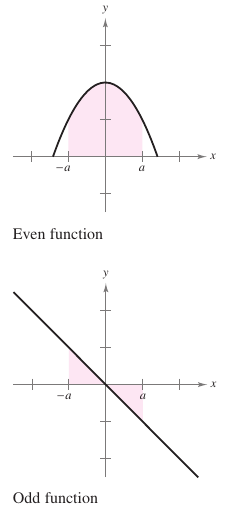
Integration can be difficult even with change variables. Simplifying a definite integral's evaluation over an interval that is symmetric about the y-axis or about the origin by recognizing the integrand as an even or odd function, as shown in Figure 4.5.3. Theorem 4.5.4 Integrating Even and Odd Functions Let \(f\) be integrable on the closed interval \([a,-a]\). 1. If \(f\) is an even function, then $$\int_{-a}^{a} f(x)\:dx$$ $$=2\int_{0}^{a} f(x)\:dx.$$ 2. If \(f\) is an odd function, then $$\int_{a}^{-a} f(x)\:dx$$ $$=0.$$ Proof Proving the first property. Because \(f\) is even, then \(f(x)=f(-x)\). Using Theorem 4.5.1 with the substitution \(u=-x\) produces $$\int_{-a}^{0} f(x)\:dx=\int_{a}^{0} f(-u)\:(du)= -\int_{a}^{0} f(u)\:du=\int_{0}^{a} f(x)\:dx.$$ Applying Theorem 4.3.3 produces $$\int_{-a}^{a} f(x)\:dx$$ $$=\int_{-a}^{0} f(x)\:dx+\int_{0}^{a} f(x)\:dx$$ $$=\int_{0}^{a} f(x)\:dx+\int_{0}^{a} f(x)\:dx$$ $$=2\int_{0}^{a} f(x)\:dx.$$ Proof for the second property is left as an exercise.

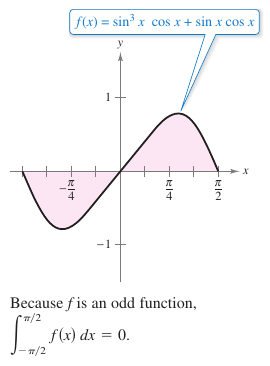
Example 4.5.10 Odd Function Integration

Figure 4.5.4

Evaluate the definite integral $$\int_{-\pi/2}^{\pi/2} ( \sin^3 x \cos x+ \sin x \cos x)\:dx$$ Solution Letting \(f(x)=\sin^3 x \cos x+ \sin x \cos x\) produces \(f(-x)\) \(=\sin^3 (-x) \cos (-x)+ \sin (-x) \cos (-x)\) \(=-\sin^3 x \cos x- \sin x \cos x\) \(=-f(x).\) Therefore \(f\) is an odd function. Because \(f\) is symmetric about the origin over \([-\pi/2,\pi/2]\), applying Theorem 4.5.4 produces $$\int_{-\pi/2}^{\pi/2} ( \sin^3 x \cos x+ \sin x \cos x)\:dx$$ Note the two regions on either side of the \(y\)-axis have the same area, as shown in Figure 4.5.4. However, because one lies below the \(x\)-axis and one lies above it, integration produces a cancellation effect.

Internal Links

Parent Article: Calculus I 04 Integration